分布式通信与并行策略

1.通信方式(NVIDIA NCCL标准)

1.1 Broadcast

1.2 AllGather

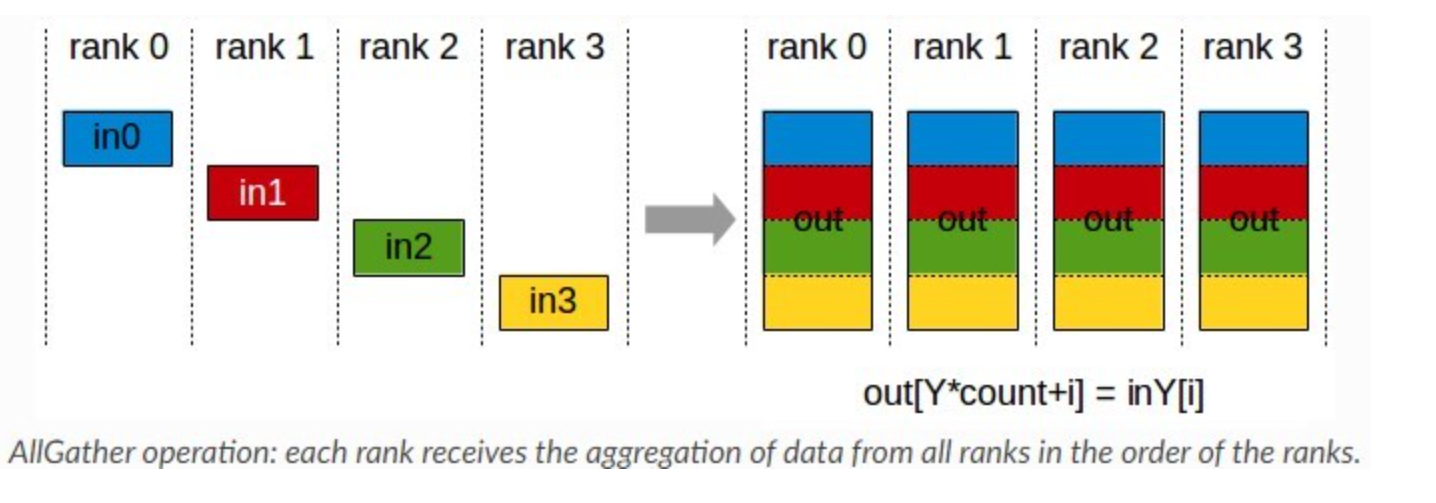
这里是使用的ring方法，即每个卡在每个时间段接收上一张卡的数据并发送当前卡的数据，每次发送第(k-1)步接收到的数据，如果k=1，即发送自己卡上的数据，经过N-1步(N为rank数)，每张卡均可得到全量的信息。

1.3 ReduceScatter

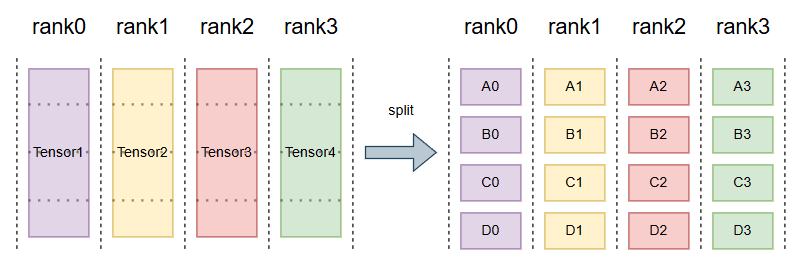
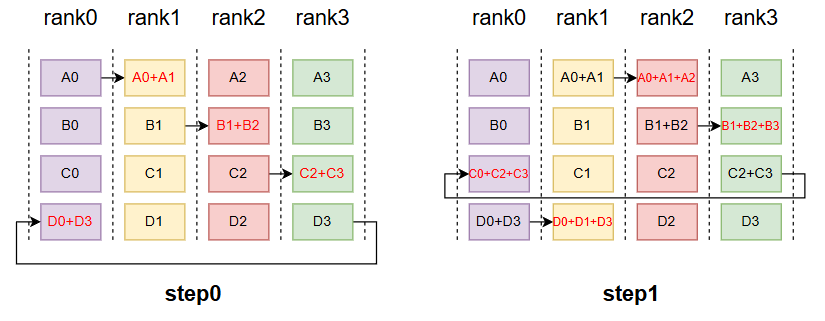
目前比较常用的就是一个ring结构；reduceScater遵循以下规则，假设有n 个rank，首先会将每个rank上的tensor，切分成个块，紧接着将其按照如下规则，每一个时间步，都按以下规则发送和接收块tensor，并且接收的块做reduce，最终rank_i得到了第(rank_i+1)%num_ranks的结果。

规则：

第 k 步 (k 从 0 到 N-2, 这里 N=4)：

发送：将本地缓冲区的第 (rank - k) % N 块发送给下一个邻居（rank+1）。
接收：从上一个邻居（rank-1）接收一个数据块，并把这个数据块与本地缓冲区的第 (rank - k - 1) % N 块相加（Reduce）。

1.4 Reduce

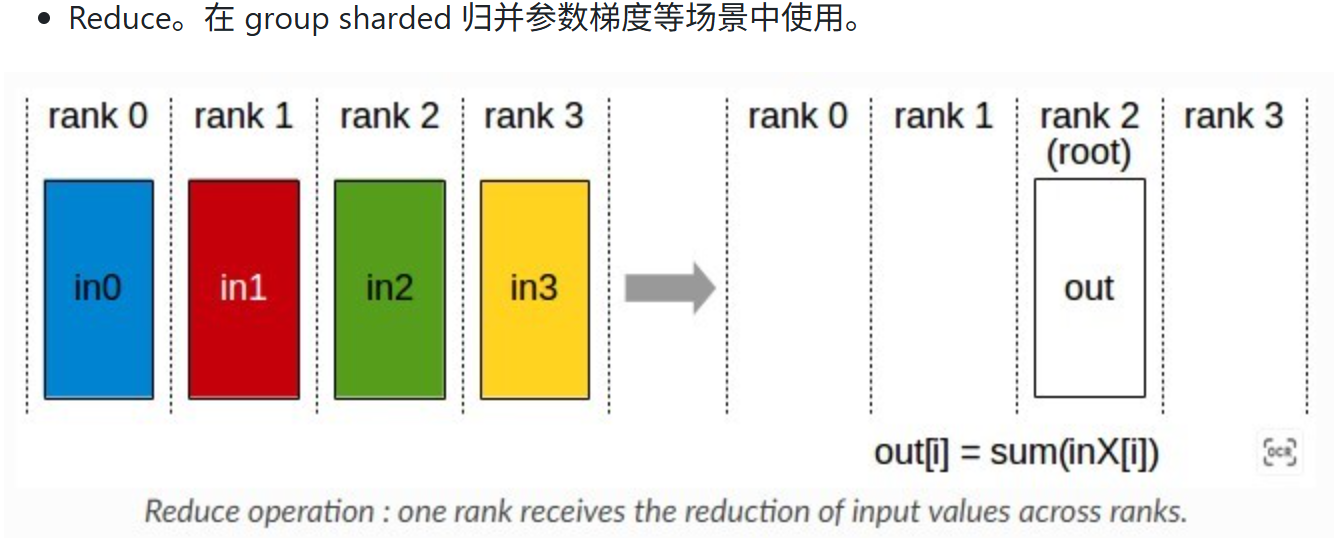
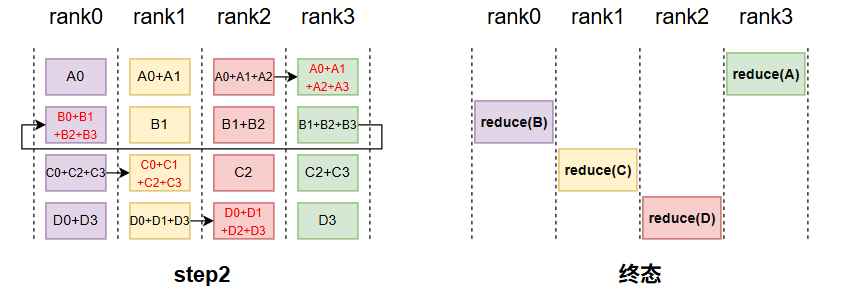
reduce的ring实现方法是reduce_scatter+p2p，即先进行reduce_scatter每张卡保留部分数据，然后直接进行p2p通信，都把自己卡上的数据发送给root。

1.5 AllReduce

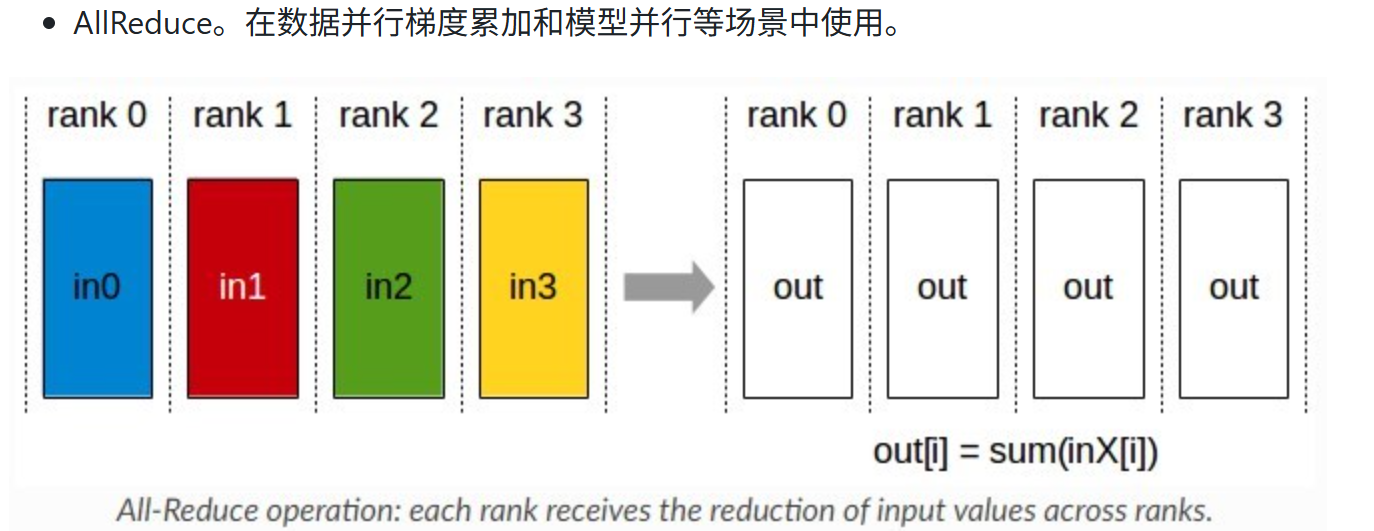
Allreduce的底层一般分为两种实现，一种是ring，一种是tree，当然还有蝶形的，因为前面两者用的比较多，所以主要了解的是前两个。

首先环状结构的实现其实就是reduce_scatter+allgather的组合，先进行(n-1)步的reduce_scatter，每个rank发送(rank-k)%N块的数据给相邻的下一个rank，k表示步数，并且从上一个rank接收数据，并将此数据加在(rank-k-1)%N块数据上，也就是做reduce，最终每个rank都有完整out的部分块，并且合并起来就是完整的out，此时再做一个allgather即可让每个rank都得到完整out，总步数为2(n-1)。特点：带宽利用率高，每一时刻所有rank都在收发数据，但延迟较高。

其次是树状结构的实现，这个主要是解决Ring在大规模节点下延迟过高的问题，适合节点极多或中小数量的场景。它将节点组织成二叉树，叶子节点把数据发送给父节点，直到根节点，即可拿到全局数据，然后使用Broadcast(向下广播)，把总和发送给子节点。特点：带宽利用率低，且越接近根节点，通信压力越大，但延迟低，为2log2(N)。

当tensor小，节点数多，延迟高时，用tree，反之用ring。一般GPU用NV Link通信，都是用ring比较多。

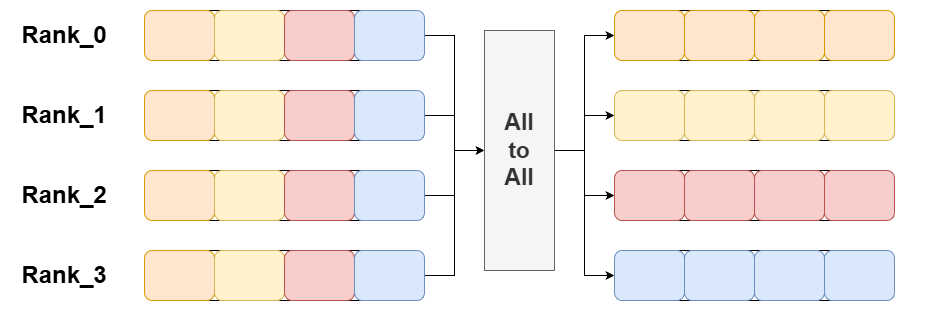
1.6 All-To-All

All-To-All 将每个参与进程将其数据分割成 N 份（N 是参与进程的总数），并将第 i 份发送给第 i 个进程。每个进程都会向其他所有进程发送数据，并从其他所有进程接收数据。如下图，All-to-All的底层实现是用P2P实现，即点对点通信：

1.7 总结

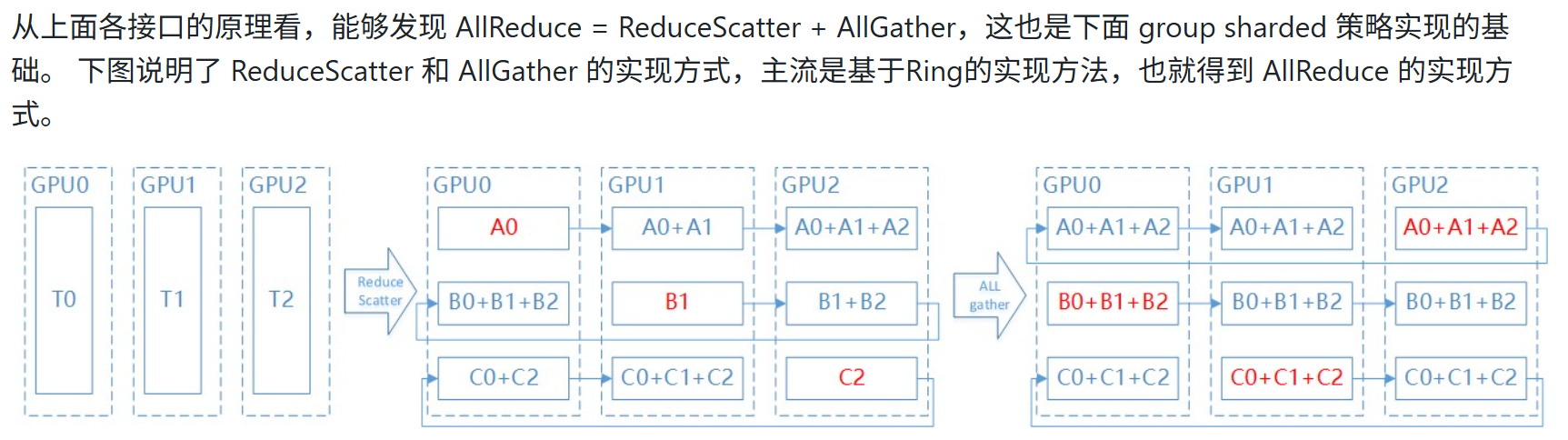
这里怎么理解AllReduce = ReduceScatter + AllGather，主要是因为ReduceScatter 把每张卡的值汇总起来，做reduce(可能是sum，average等)，然后把结果分成rank个sub_result部分，分别给每个rank，而AllGather再把这rank个sub_result给聚合起来到每个rank上，则每个rank都有完整的result。其机制就跟直接做allreduce一样，对每个rank的数据汇总做reduce，然后把result分到每个rank上。

reduce_scatter使得每个rank_i获得了第(rank_i+1)%num_ranks的结果。这是需要n-1步，然后all gather需要把每张卡上reduce的结果，分发到其它卡，再走n-1步，所以一共的通信步是2*(n-1)。

2. Paddle三类通信区分动手，动半，静态全自动

同时，在动手的案例中不会出现dist_tensor，shard这些东西，因为这是动半特有的，对通信进行标记使用shard，而tensor被shard处理后，即变成了dist_tensor。

3.分布式并行方式

分布式并行方式包括：数据并行(DP),张量并行(tp),流水并行(pp)，专家并行(ep)，序列并行(sp)，上下文并行(Context Parallel)

3.1 数据并行。

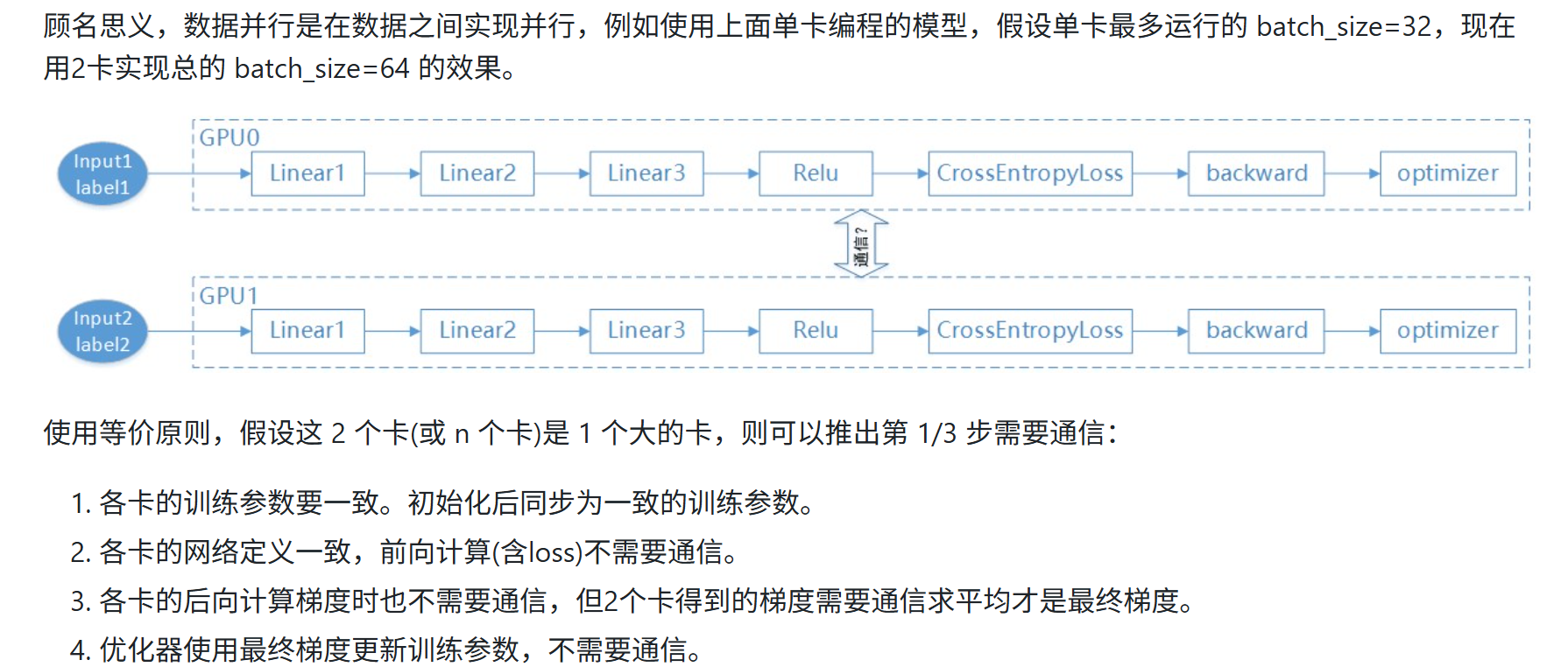
1通信为了让数据并行模型参数保持一致，3通信是为了让梯度累加；在反向过程中，本层的∇x梯度计算完毕后，可以继续计算下一层的∇x梯度，而不需要等待∇w的梯度计算，做∇x梯度的计算时，又可以做∇w的allreduce通信，从而达到通信与计算重叠。

必须注意，∇x不需要做allreduce，只有∇w需要，因为∇w做allreduce是为了同步每一份相同参数的grad，最后更新后的参数也在DP组间保持一致，而∇x两张卡上是分别不同的batch数据计算得来的，没有数学依赖关系。

注意： 数据并行分两种，上面是DDP，即Distribute_DP是基于多进程实现的，还有一种是DP，是单进程多线程实现，如下图所示，它使用一个进程来计算模型权重。

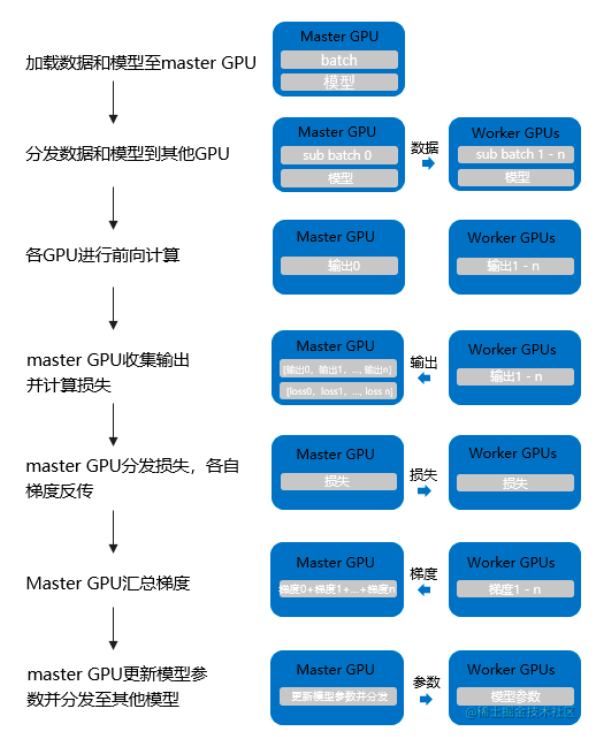
注意： 二者效果是等价的，因为假设我们DP实现batchsize为64的数据量，对于DP来说，它会在计算loss时，汇总64条数据的output，然后和lable计算出loss，并得到一个平均的loss，再传给各GPU进行反向传播，此时每个grad就是平均之后的，即除以了64的。而DDP 则分给两个GPU各自去计算梯度，每个GPU计算的梯度也是mean的，不过是除以32的，所以要再allreduce一下，两个相加除以2，即同样是除以64。

补充说明：ZeRo(DeepSpeed,微软提出) 以及FSDP(Pytorch最新数据并行方案，ZeRo3和FSDP思想等价)

Group Sharded：

（这里存在一个组shard的概念，即按param的属性，将其划分到一个group，这些param在group里面同步和通信，与其它group相对独立，可以看一下记录的Dynamic optimizer shardingV1,V2的Fused_Buffer的概念）

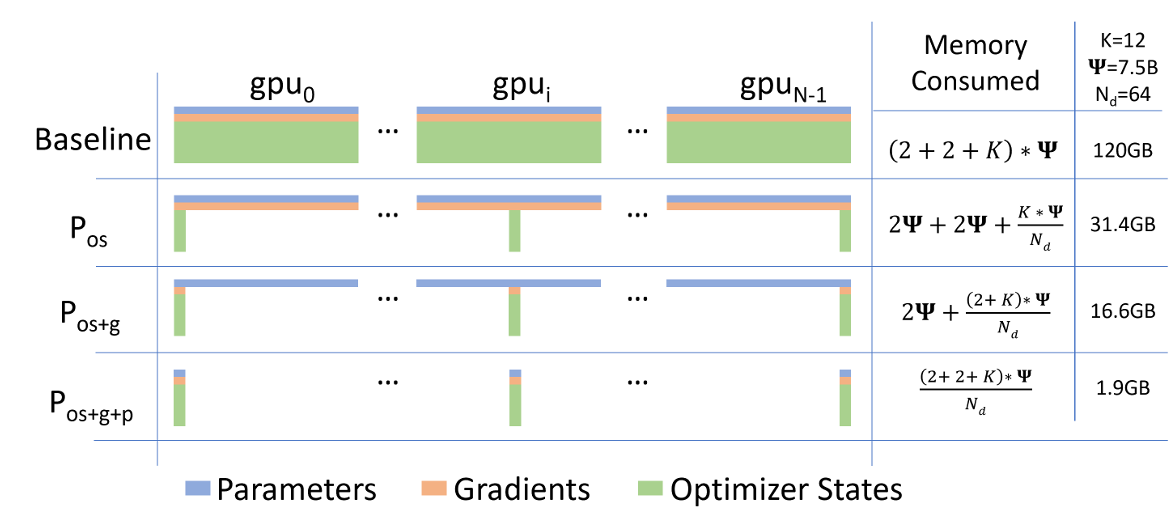
ZeRO-1(pytorch:OSS)：

ZeRO-1没有将模型本身进行分片，也没有将Gradient进行分片，而是只将优化器进行分片。训练过程与DDP类似。

forward过程由每个rank的GPU独自完整的完成，然后进行backward过程。在backward过程中，梯度通过allReduce进行同步。
Optimizer state 使用贪心策略基于参数量进行分片，以此确保每个rank几乎拥有相同大小的优化器内存。
每个rank只负责更新当前优化器分片的部分，由于每个rank只有分片的优化器state，所以当前rank忽略其余的state。
在更新过后，通过广播或者allGather的方式确保所有的rank都收到最新更新过后的模型参数。

ZeRO-1 非常适合使用类似Adam进行优化的模型训练，因为Adam拥有额外的参数m（momentum）与v（variance），特别是FP16混合精度训练。ZeRO-1 不适合使用SGD类似的优化器进行模型训练，因为SGD只有较少的参数内存，并且由于需要更新模型参数，导致额外的通讯成本。ZeRO-1只是解决了Optimizer state的冗余。

ZeRO-2(pytorch:SDP)：

相比于ZeRO-1，ZeRO-2除了对optimizer state进行切分，还对Gradient进行了切分。

像ZeRO-1一样将optimizer的参数进行分片，并安排在不同的rank上。在backward过程中，gradients被reduce操作到对应的rank上，取代了all-reduce，以此减少了通讯开销。每个rank独自更新各自负责的参数。在更新操作之后，广播或allGather保证所有的ranks接收到更新后的参数。

ZeRO-3(pytorch:FSDP)：

为了进一步节省更多的内存，ZeRO-3提出进行模型参数的分片。类似以上两种分片方式，ranks负责模型参数的切片。可以进行参数切片的原因主要有以下两点：

All-Reduce操作可以被拆分为Reduce与allgather操作的结合。
模型的每一层拥有该层的完整参数，并且整个层能够直接被一个GPU装下。所以计算前向的时候，除了当前rank需要的层之外，其余的层的参数可以抛弃。从这个层面上来说，Zero相当于数据并行+模型并行。

FSDP(Fully Sharded Data Parallel)：

FSDP 是一种新型数据并行训练方法，但与传统的数据并行不同，传统的数据并行维护模型参数、梯度和优化器状态的每个 GPU 副本，而 FSDP 将所有这些状态跨数据并行工作线程进行分片，并且可以选择将模型参数分片卸载到 CPU。

下图显示了 FSDP 如何在 2 个数据并行进程中工作流程：

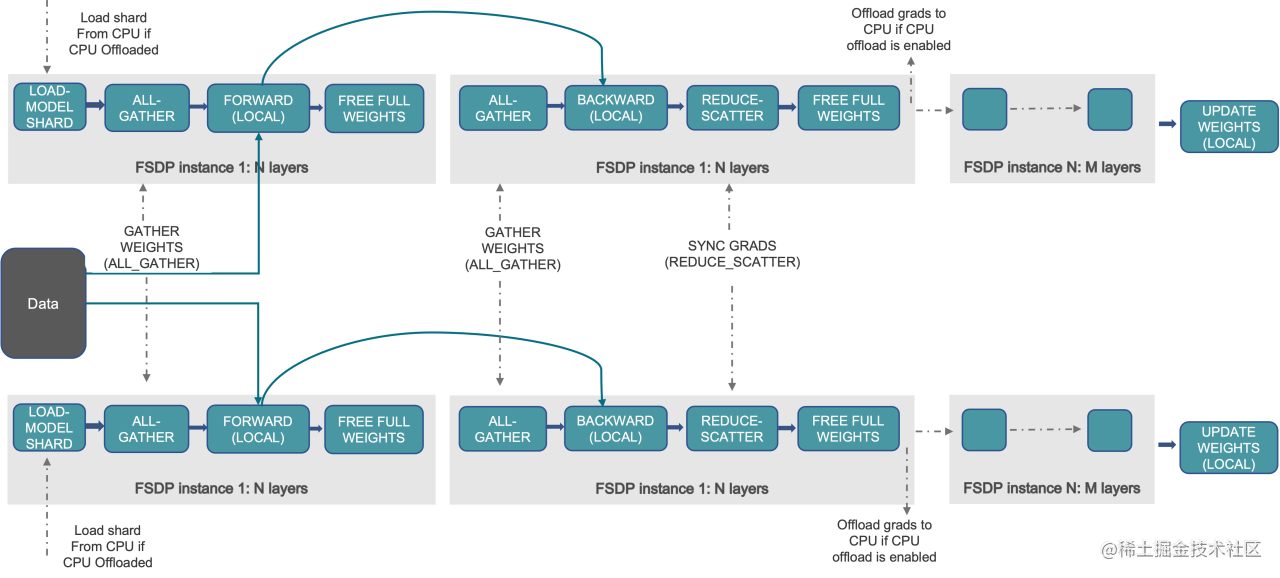
通常，模型层以嵌套方式用 FSDP 包装，因此，只有单个 FSDP 实例中的层需要在前向或后向计算期间将完整参数收集到单个设备。计算完成后，收集到的完整参数将立即释放，释放的内存可用于下一层的计算。通过这种方式，可以节省峰值 GPU 内存，从而可以扩展训练以使用更大的模型大小或更大的批量大小。为了进一步最大化内存效率，当实例在计算中不活动时，FSDP 可以将参数、梯度和优化器状态卸载到 CPU。

3.2 张量并行(TP,MP)

1 基础并行层

1.1 ColumnParallelLayer与RowParallelLayer同时使用的关系

ColumnParallelLayer

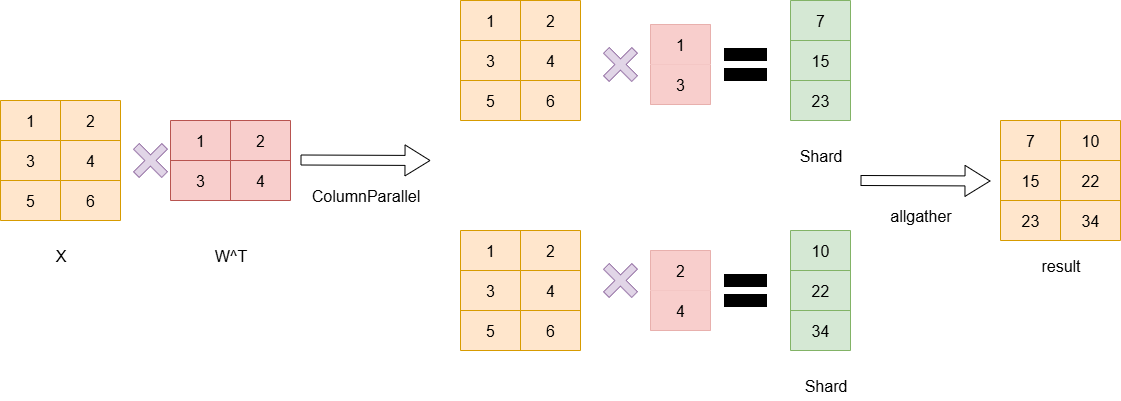
columnparallel.drawio

RowParallelLayer

Rowparallel.drawio

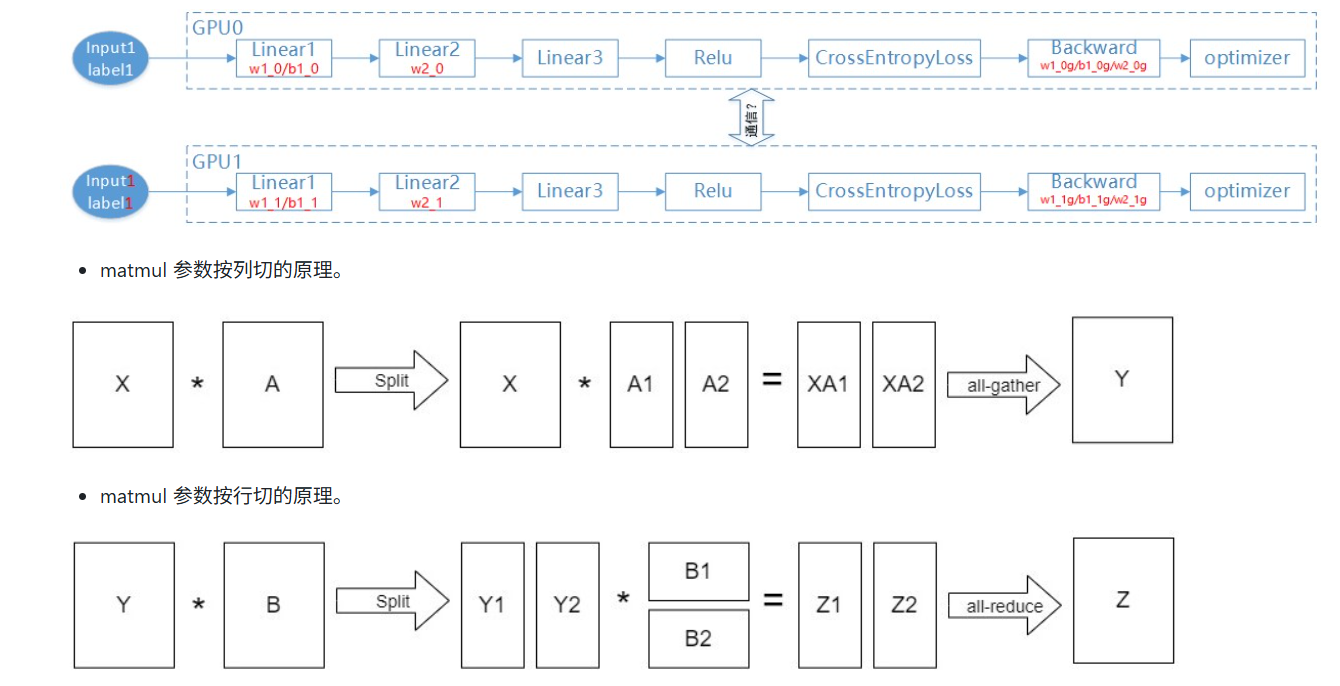
可以看到，RowParallelLayer在计算的过程中，需要把输入拆分成两列分别在两张卡上做计算，最终两张卡都得到Parital状态的数据，而如果上一层是ColumnParallel则其计算的结果刚好分配到两个设备上(即结果被按列切分)，而此结果正是RowParallelLayer需要的输入，那么就无需做通信，直接继续计算最后再做allreduce即可。

1.2 ColumnParallelLayer与RowParallelLayer的w和bias的切分

层间计算.drawio

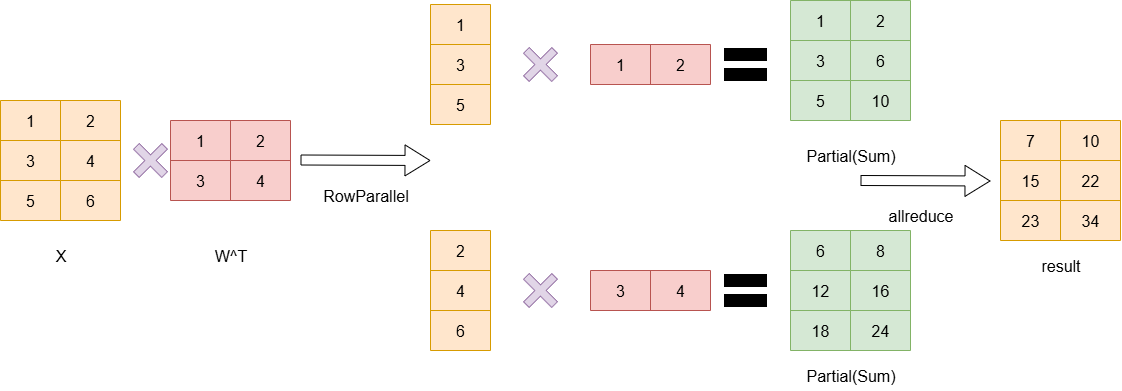
注意，在做y=x*W^T+b的计算时，首先乘积得到的数据是[batchsize,output_size]，每一行表示一个数据，而bias是分别和每一行相加，因此bias是一个一维的向量，因此，当W按列切分时，bias需要按行切分，从而保持正确的计算关系。

当添加了bias的时候，做RowParallelLayer和ColumnParallelLayer情况如下：

RowParallelLayer：

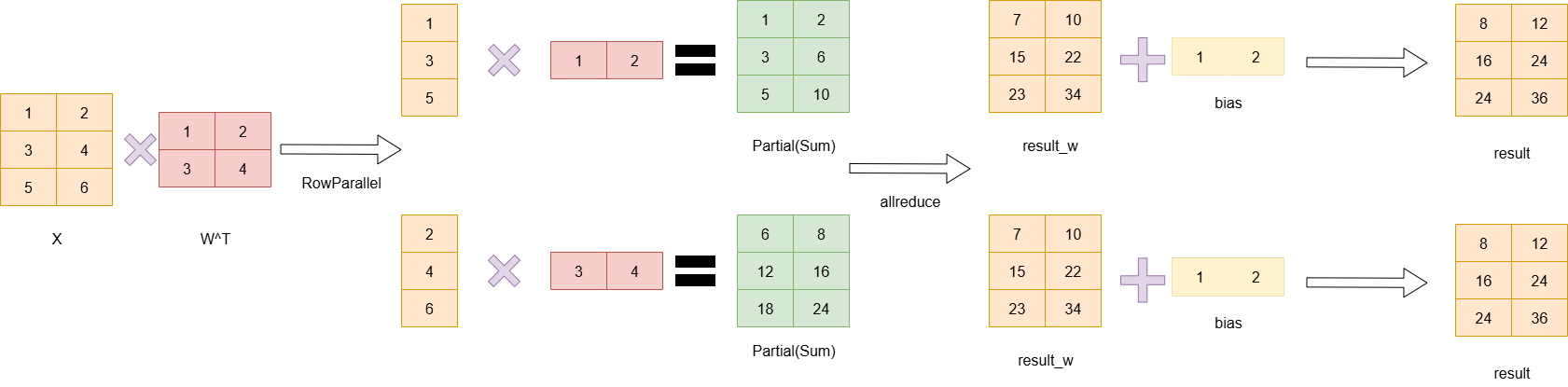
RowParallel_bias.drawio

RowParallelLayer只切w，不切bias

ColumnParallelLayer：

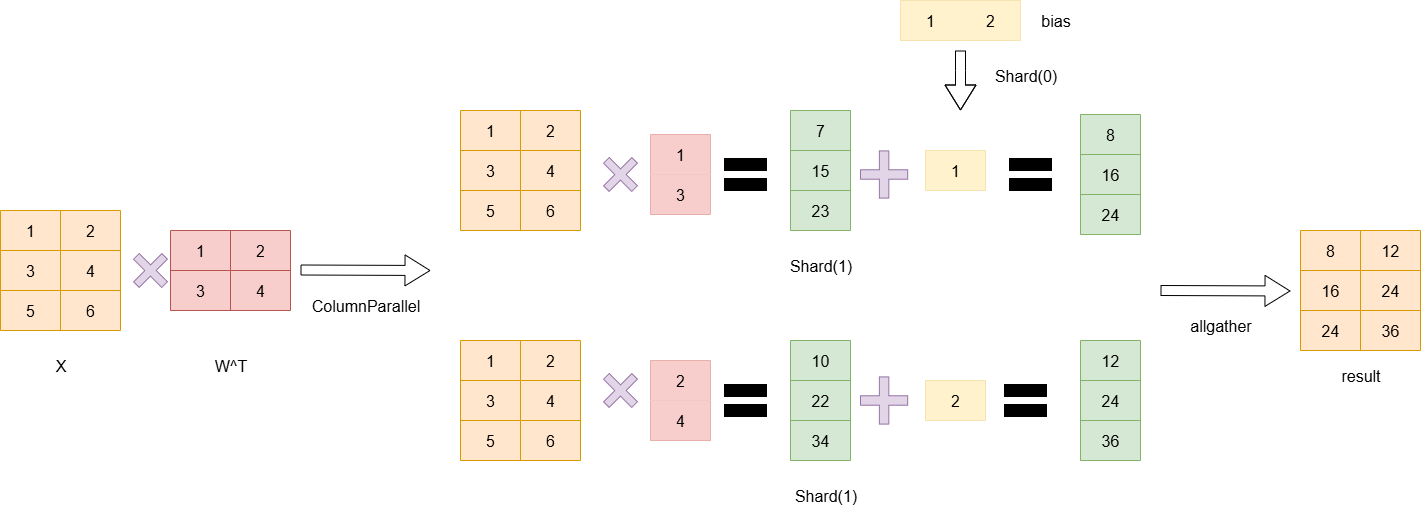
ColumnParallel_bias.drawio

ColumnParallelLayer切w的axis=1，切bias的axis=0

1.3 Vocab Parallel Embedding

Vocab Embedding

示例：

文本输入

用户输入: "Hello world, how are you?"

分词（Tokenization）

分词结果: ["Hello", "world", ",", "how", "are", "you", "?"]

词汇表映射（Vocabulary Mapping）

词汇表: {"<PAD>": 0, "<UNK>": 1, "<BOS>": 2, "<EOS>": 3, 
         "Hello": 4, "world": 5, ",": 6, "how": 7, "are": 8, "you": 9, "?": 10, ...}

映射结果: [4, 5, 6, 7, 8, 9, 10]

输入到模型为词汇ID序列

模型接收的输入: x = [4, 5, 6, 7, 8, 9, 10]  (词汇ID序列)

因此，Vocab Embedding接收到的输入x是[batch_size,seq_length]，即多组词汇ID序列。Vocab Embedding的大小为(vocab_size,hidden_dim)，vocab_size这个维度即表示了所有token的ID，根据token_id找到对应的行，该行所有的列则表示当前这个token的向量化表示，即包含其数学维度信息的特征向量。初始时，这些数据是没有意义的，经过训练后，则可以表示每个词的空间特征，越相近的词，在空间上离得越近。

根据 x，在vocab表中查找对应token的向量化表示，最终输出为[batch_size,sequence_lenth,hidden_dim]。

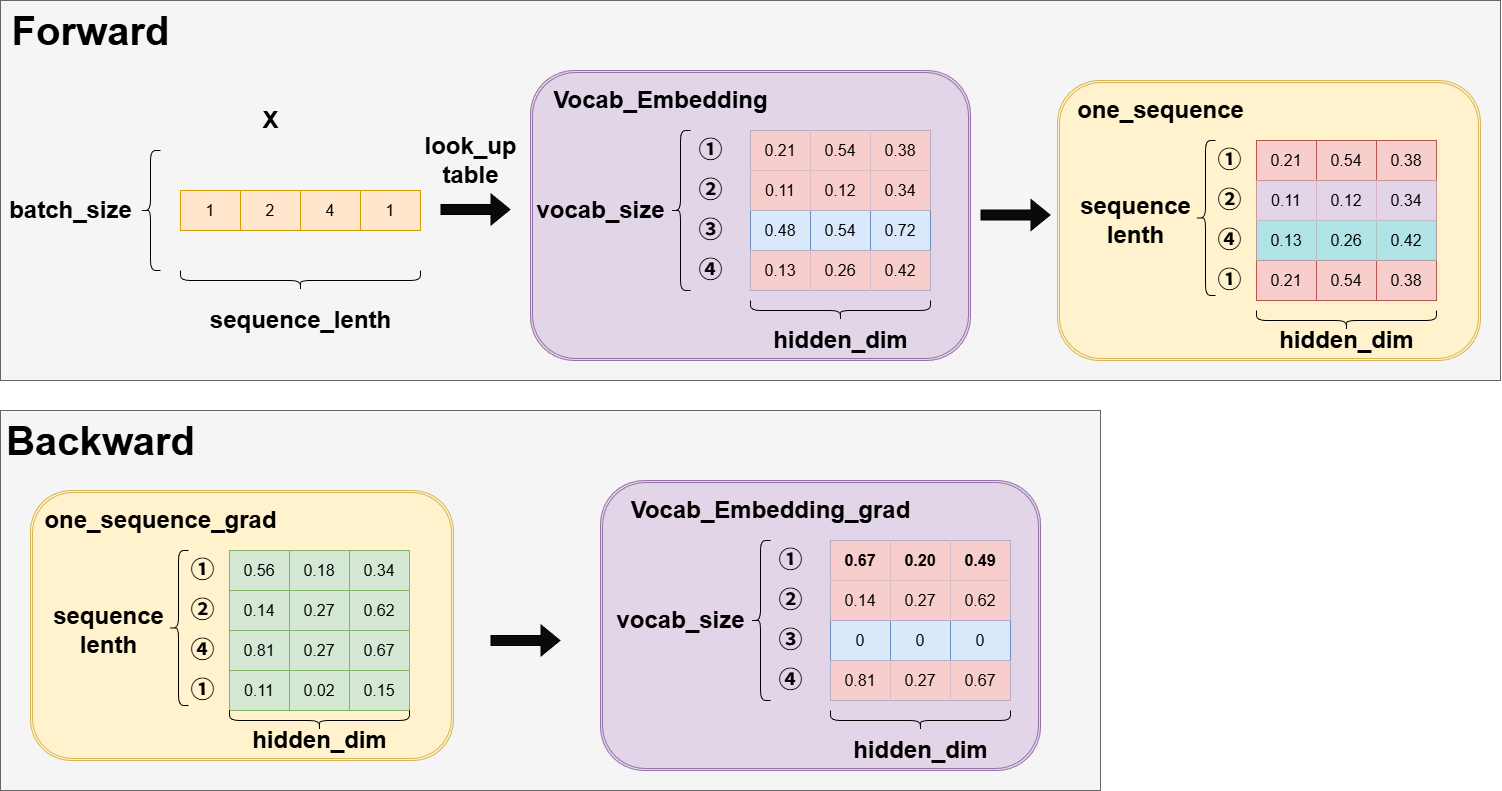
Vocab_embedding.drawio (3)

如图，以batch_size=1为例，查表后，通过当前输入的sequence_lenth中存在的token_ids，选择k行，最终构成[batch_size,sequence_lenth,hidden_dim]的输出。

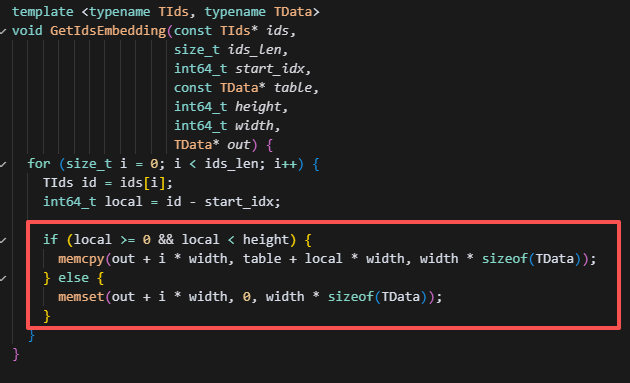
反向的grad形状与forward输出时形状相同，而因为Vocab_Embedding的操作是从整个词表中选出k行数据，因此最后更新grad的时候，也是指有这k行数据有grad，而其它行均默认为0，若有相同token_id，则做梯度累加。

Vocab Parallel Embedding

如果是词表并行，则按vocab_size维度做切分，多路并行时，在forward阶段需要做all_reduce，因为只在本rank的词表查找，若查找到，则返回词表的这一行值，即当前token的向量化表示；若超过此范围，则返回的是默认值0。all_reduce之后，每个rank都能拿到全部token的向量化表示。反向梯度更新的时候无需通信，直接选当前rank的词表范围内的梯度进行累积，并更新词表对应行的数据即可。

一般来说，输入层和输出层共用一个word embedding，所以在backward过程，我们会分别对输入，输出层做一次梯度计算，而最终更新embedding的时候应该是两次梯度的总和，所以如果是TP没什么问题，因为TP下，输入和输出层都在一个GPU上，而当PP时，会分在不同卡上，这时候就需要对两卡的word embedding 梯度做一次all reduce。

1.4 输出层的 Vocab Embedding

输出层的vocab embedding和输入层的操作刚好相反，输入层是将对应的token_id的embedding数据取出，即将seq_len扩展成 $seq\_len*embedding\_dim$ ，而输出层的vocab embedding则是将embedding映射回词表，即变成 $seq\_len*vocab\_size$ 。推理的话只需要取seq_len的最后一行的数据，做softmax即可。具体计算如下：

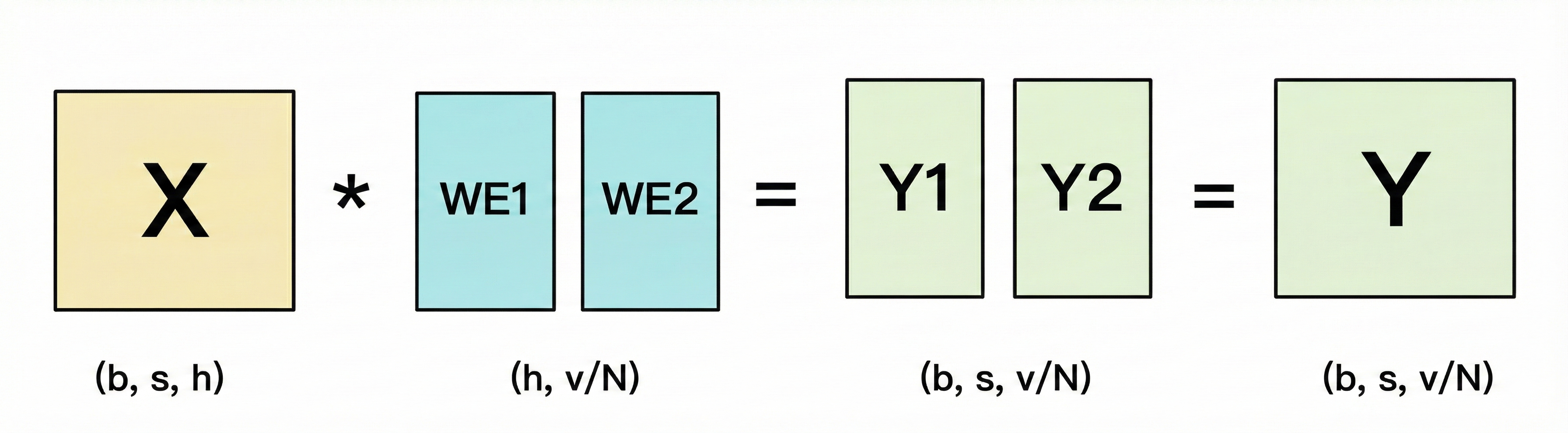
Gemini_Generated_Image_gx9vjwgx9vjwgx9v

可以发现，这时候得到的Y1,Y2是Y被列切的状态，我们可以用all_gather去让每个rank得到完整的Y，但是这样做的单卡通信量是 $b*s*\frac{v}{N}*(N-1)$ ，所以为了减少计算量，Megatron并不用allgather做实现，而是用allreduce，如下方法：

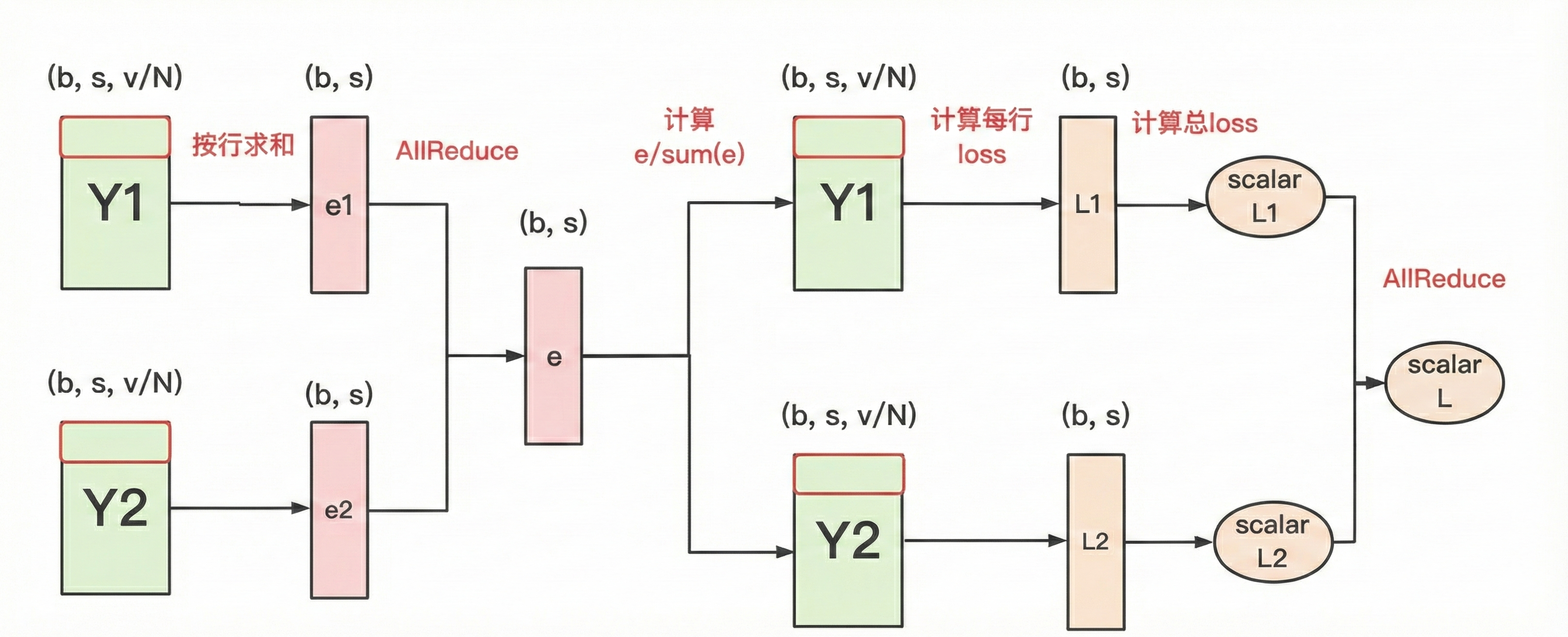
Gemini_Generated_Image_vduuvevduuvevduu

将每个rank上的输出Yi按行求和，此时得到的是局部和，再做一个allreduce，则得到全局和，有了全局和，就可以做softmax计算每个Yi每一行logits的概率，并按行计算loss，这里计算loss，比如当前预测的token前[1,v/2]，而在rank2上就会发现找不到这部分的概率，即这一行预测值和真实标签计算Cross Entropy的时候会出现全0，但是这一半在rank0上算了，而Cross Entropy本身也就只有一个位置是有值的（其它标签都为0，相当于没值）所以做一个allreduce即可得到最终的全局loss。

那么就可以发现，此时的单卡通信量就是 $(b*s+b)$ ，一条数据一个loss，所以loss的通信量是b。

2.TP的forward与backward过程

通信分析(行列切的详细分析可以见基础并行层)：

1.初始化：

各卡训练参数为partial状态，即部分参数，对于切分的参数，分别初始化；对于没有切分的参数，初始化后同步为一致的参数（此时需要通信同步）。

2.Forward

各卡的网络使用切分后的网络，即网络层数不变，但shape为切分后的shape。如果是column parallel，则得到的每个rank的output也是经过了column parallel的output，因此需要做allgather，将输出拼接；而如果是row paralle，则得到的每个rank的output，形状与output相同，但数据属于partial状态，需要做all-reduce获得完整张量。

看上图，假设Linear1是ColumnParallel，Linear2是RowParallel，则列切计算出来后的结果，可以直接作为行切的输入(如果tp数相同，即Y1,Y2)，因此无需通信(注意，若此时下一层做全参数计算，而不是RowParallel，则需要做all-gather聚合输出，拼接成完整的输出Y)，而Linear2的结果要作为完整参数输入到Linear3（和单卡视角对齐），因此需要对Z1,Z2做allreduce，得到完整输入Z。这里需要做一次通信。

3.Backward

在反向传播过程中，因为Linear3以后的层都是完整参数，所以纯TP下，反向计算的梯度都是一样的，无需通信，

Linear2的反向梯度计算：

完整参数下：

$\frac{\partial L}{\partial B}={Y^T}*\frac{\partial L}{\partial Z}$

$\frac{\partial L}{\partial Y}=\frac{\partial L}{\partial Y}*B^T$

而由于卡1和卡2分别占据部分参数B1、B2,因此只需要B1、B2部分参数分别对应的梯度即可(Y1,Y2分别是卡1，卡2此时的输入，因此分别计算自己卡上的数据，无需通信)：

即 $\frac{\partial L}{\partial B_1}=\frac{\partial L}{\partial Z}\frac{\partial Z}{\partial B_1}=\frac{\partial L}{\partial Z}\frac{\partial Y_1B_1}{\partial B_1}=Y_1^T\frac{\partial L}{\partial Z}$

同理，B2的梯度也是,所以求B1的梯度无需通信。

对于输入Y，由于对称性，可知：

$\frac{\partial L}{\partial Y_1}=\frac{\partial L}{\partial Z}\frac{\partial Z}{\partial Y_1}=\frac{\partial L}{\partial Z}\frac{\partial Y_1B_1}{\partial Y_1}=\frac{\partial L}{\partial Z}B_1^T$

Y2同理，此时计算出来的梯度无需通信，因为Y1,Y2即分别对应rank0，rank1的上一层Linear1的输出，上一层也是切分状态，所以，求输入的梯度Y1,Y2也无需通信。注意：若上一层为完成的参数做forward，即rank0，rank1输入都是完整的Y，则backward时，需要做allgather将Y1_grad，Y2_grad做聚合

Linear1的反向梯度计算：

X*A1=Y1,X*A2=Y2

则 $\frac{\partial L}{\partial A1}=X^T*\frac{\partial L}{\partial Y1}$

每个rank都有全量X，因此也无需通信。

但是，如果X需要继续传播梯度：

对于rank1： $\frac{\partial L}{\partial X}=\frac{\partial L}{\partial Y1}*A_1^T$

对于rank2： $\frac{\partial L}{\partial X}=\frac{\partial L}{\partial Y2}*A_2^T$

此时两个rank的 $\frac{\partial L}{\partial X}$ 是partial的状态，因此需要做allreduce，才能得到X的完整梯度。如果要继续往下传递grad，且接下来的参数都是未切分的，则这里需要做all-reduce通信合并成完整梯度。

4.Optimizer

每张卡获得grad后，在optimizer中进行参数更新，无需通信。

3.Megatron中TP的使用

通常MLP层是两个FFN，则都是列切和行切配对实现的，即TP层一般输入都用列切接收，并用行切处理后，再输出结果。即TP处理后的模型层，最终输出是一个partial的状态，需要做all-reduce来累加得到全局结果，但是每个rank上的形状都完全一样。MLP层切分的维度即model_dim

而对于Attention层来说，正好存在多头注意力机制，而每个头的self-attention计算是独立的，因此TP可以直接按照头的维度切分。

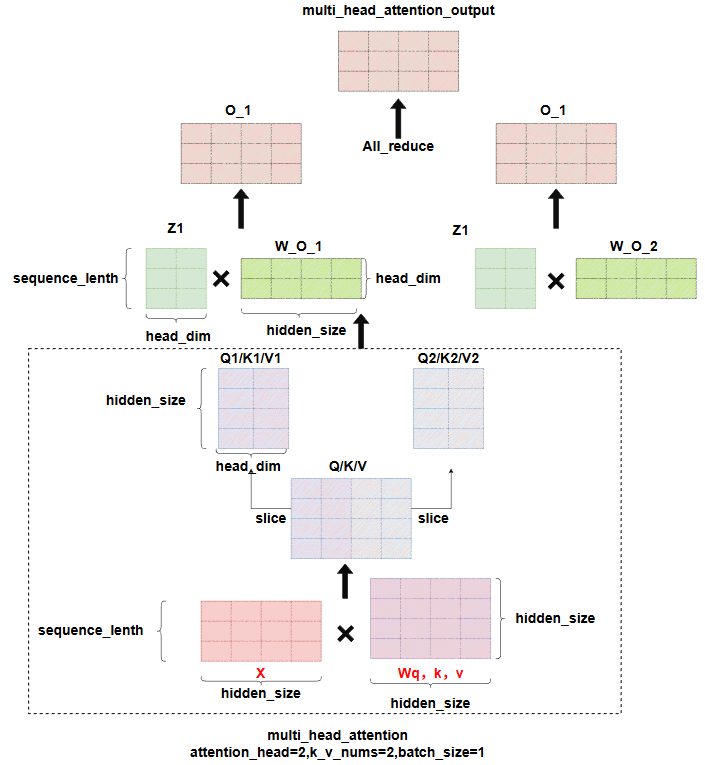
注意，一般multi-head-attention，在单卡计算时，是多个attention score(已经和V矩阵计算完)计算完成后，拼接成一个大的矩阵，再和输出的Wo矩阵做计算，得到最终的输出，但是在TP下，如果仍然按这个操作，会导致每张卡上都保留有一个完整的Wo矩阵的副本，浪费显存，因此megatron把Wo矩阵也按head的维度做了切分，则每个tp rank上算出来的输出O，均是一个partial的状态，经过一次all_reduce即可得到完整的输出，这就是为什么这里是all_reduce通信而不是allgather。

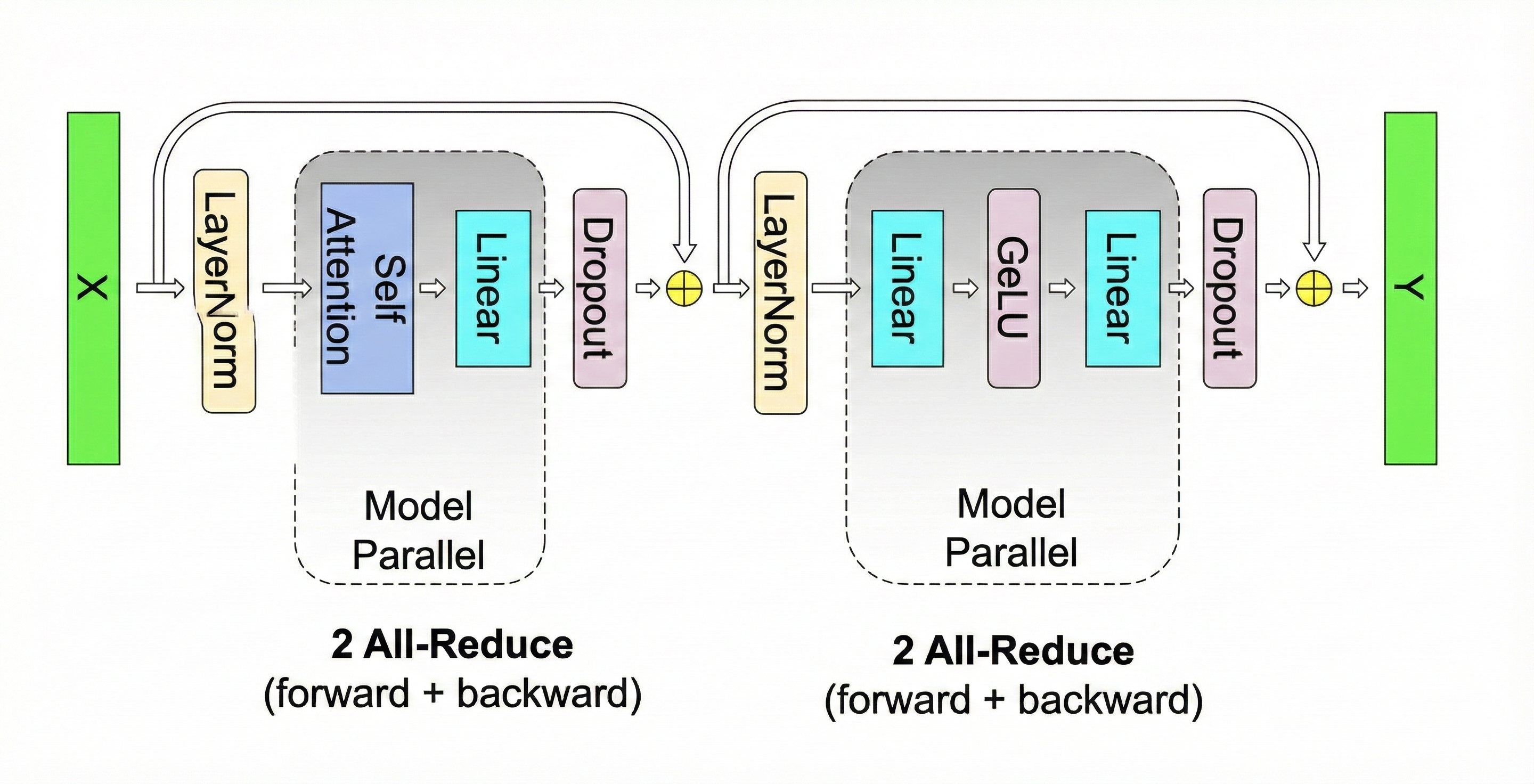
Gemini_Generated_Image_az5pw3az5pw3az5p

如图即为TP下一层Attention+一层MLP层的forward的过程。在整个前向+反向共4次all-reduce。

DP与TP混合时，由于DP每一层之间没有通信依赖，即当前层做allreduce时，可以继续算下一层的梯度，而对于TP来说，它计算完当前层的grad，需要卡间做allreduce后，得到全局的grad，才能继续下一层的梯度计算，因此DP和TP混合时，最好将TP放在同一台机器，DP可以看情况放在多条机器间，从而提高效率。

3.3 流水并行(PP)

流水并行是在模型层间实现并行，以层为粒度将不同的层和参数划分到不同卡上并行计算。如上图所示，将Linear1和Linear2切分到0号卡，Linear3和Relu切分到1号卡。流水并行钟，loss层和准确率计算都在前向计算的最后1卡上，也仅有这张卡上能获取到loss值。

同样进行通信分析：

1.各卡的训练参数按流水线切分后的参数分配，分别初始化，不需要通信。

2.各卡的网络使用切分后的网络，在前向计算中，当前卡计算完成后的数据要send到下一阶段的卡上，同时需要从其它卡通过recv接收数据。此时需要通信。

3.反向计算过程与前向一样，需要发送和接收grad数据，因此也需要通信。

4.由于optimizer不做切分，因此各卡都有完整优化器，用于更新参数，无需通信。

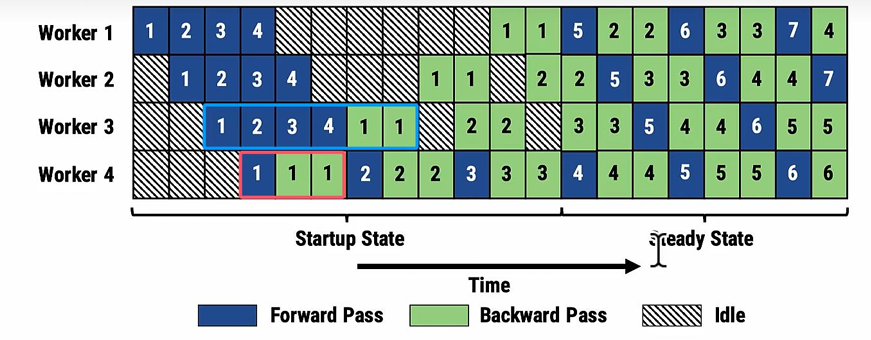
流水并行的基本示意图如下：

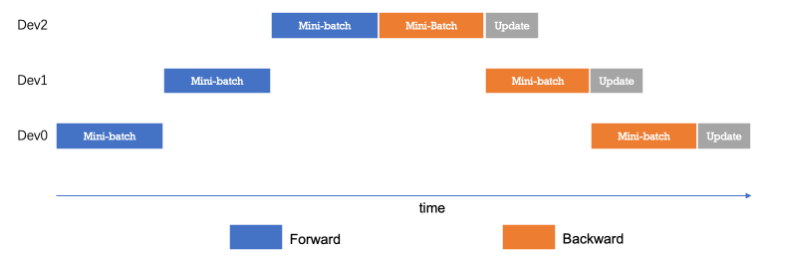
而为了优化流水线并行中设备的计算效率，可以进一步将mini-batch切分成粒度更小的micro-batch，来提升流水并行的并发度，进而达到提升设备利用率和计算效率的目的。如下是以更小粒度的micro-batch做编排：

FthenB

上图这样的方法是最基础的micro-batch方法。即先做forward，所有forward做完再做backward。假设forward和backward的时间分别是tf，tb，并且共有m个micro_batch，则理想的流水并行时间为：

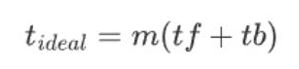
但是注意，由于pp并行设备会经过warmup和cooldowm阶段，即存在设备空转的时期，因此导致并不是每时每刻所有设备都在处理micro_batch，所以实际时间还要加上空转的时间，其实就是bubble的时间。bubble占用时间：

并且FthenB存在大量activation数据被保存在显存等待backward的时候调用的问题，显存利用率很低。

1F1B编排

在此基础上，1F1B编排被提了出来，现在当第一个micro_batch做完所有的forward之后，就会立即开始做backward。

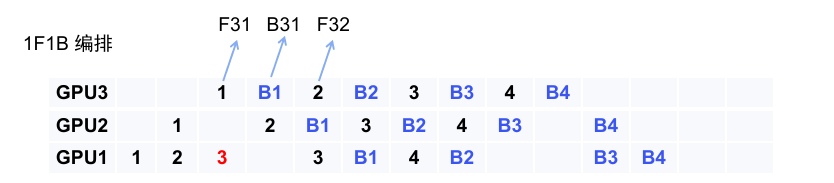
可以看到：

gpu1的峰值动态内存最多只用保存3份forward的中间变量
gpu3的峰值动态内存最多只用保存1份forward的中间变量

相比于之前的FthenB，如果现在用FthenB，则每张卡都要存4份，峰值显存相比之下降低了很多。

但是，需要注意的是，buble率并没有用下降，原因很简单，forward的时候，最后一个rank会空转直到第一个micro_batch的forward进行到最后一个模型块；而反向的时候第一个rank会空转直到第一个micro_batch的backward进行到第一个模型块，这在1F1B和FthenB中都是一样的结果。

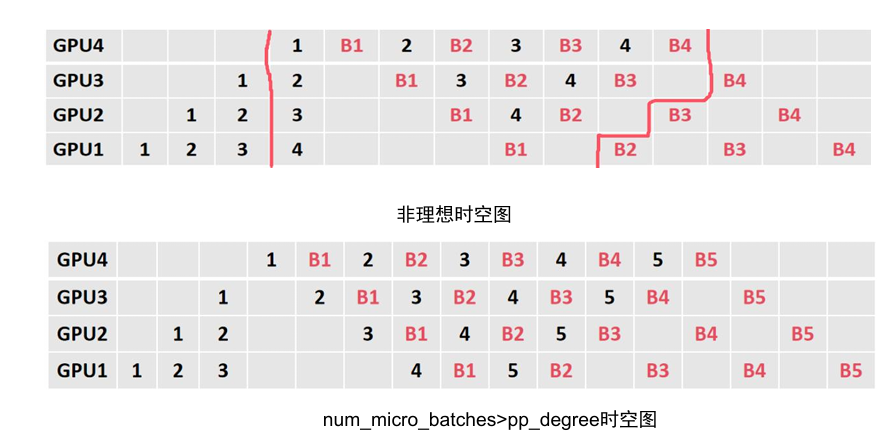
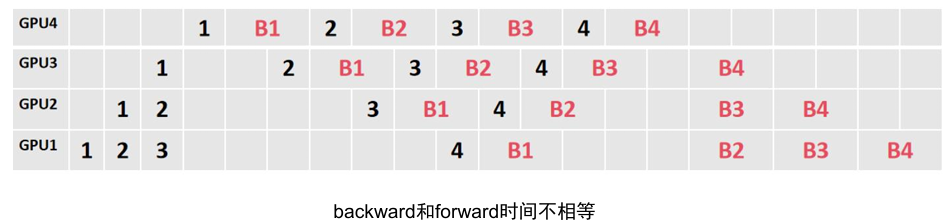
可以看到无论是非理想状态(即时空图不对称)，还是forward，backward不相等，或者num_micro_batches>pp_degree，总体上1F1B都的编排都遵循如下规律，这里设forward为f，backward为b，流水并行数为 $pp\_degree,micro\_batch$ 数为N，流水并行编排阶段号为 $pp\_stage$ ：

warmup阶段： $(pp\_degree-pp\_stage-1)f$

1F1B阶段： $(N-(pp\_degree-pp\_stage-1))f+b$

cooldown阶段： $(pp\_degree-pp\_stage-1)b$

所以1F1B和FthenB的bubble占理想时间的比例均为：(p为pp_degree数)

激活重计算

这是一种时间换空间的方法，可以看到backward是forward时间的两倍，这里表示forward过程不保留激活值，而是在backward的时候，重新推理一遍前向获取激活值，这样每张卡都不用拿多的显存来保留激活值了。

VPP

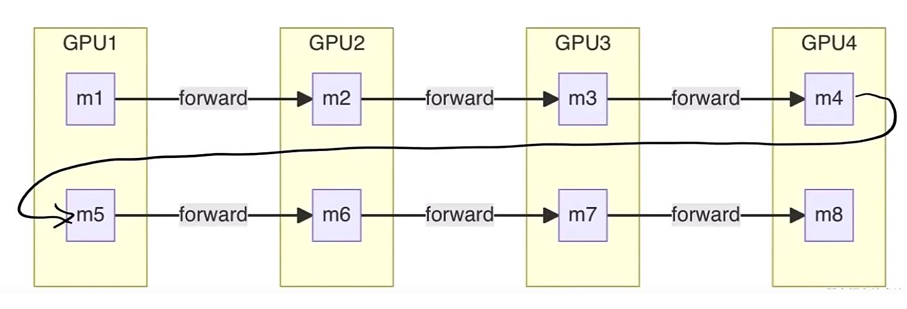
VPP是1F1B的进阶版，主要是采用Round Robin的方式把不同层按顺序依次划分到N个GPU上，即每个gpu会经过多轮的forward，才完成一次完整的前向。

从图中我们也可以看出来，VPP相比于1F1B主要做的工作其实从逻辑上看，是把原来的一个比较大块的forwrad切分成了更小的粒度，这么做的好处是，虽然编排后，bubble的率，即bubble个数占整个job编排个数的比例并没有变，但是每个bubble时间占总时间的比例变小了，原来forward一次需要tf的时间，切分成v份后，就只需要tf/v的时间，因此bubble的时间也相应减少为1/v。

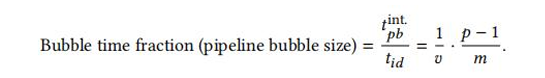
那是不是我们把模型分成更多份，让这个V越来越大，整个bubble时间越小，效率就越高呢？

答案肯定是否定的，因为这里要注意一个问题，GPU间点对点通信次数，为vpp_degree倍，切分的越多，意味着通信量成倍的上升，这也是影响性能的关键，因此不能盲目的增加vpp_degree。

VPP的编排公式如下（cool_down阶段与warm_up阶段对称，因此不需要写，注意需要判断一下total_steps和warm_up_steps的大小，）：

\text{warm\_up\_steps} = 2 \times (\text{pp\_degree} - \text{pp\_stage} - 1) + (\text{vpp\_degree} - 1) \times \text{pp\_degree}

\text{steady\_steps} = \text{acc\_steps} \times \text{vpp\_degree} - \text{warm\_up\_steps}

这里warm_up_steps的公式怎么理解呢？

这里可以拆解为两步计算如下：

1. 计算 warmup_steps 的初始值：

\text{warmup\_steps} = (\text{pp\_degree} - \text{pp\_stage} - 1) + (\text{pp\_degree} - \text{stage\_stage} - 1)

2.更新 warmup_steps：

\text{warmup\_steps} += (\text{vpp\_degree} - 1) \times \text{pp\_degree}

这里解读一下这两个公式的具体来源：

首先我们先解释公式2的由来：可以注意到，最先开始做1F1B的一定是最后一个rank，即当第一个micro_batch经过vpp_degree轮在所有rank间的循环后，它来到最后一个模型块，做最后的forward，接下来就准备开始它的backward的阶段了。所以最后一个rank一定会做(vpp_degree-1)*pp_degree步的forward（这里把最后一个模型块做forward的部分给剔除了，因为他会被算在steady阶段），既然最后一个rank会做这么多forward，那么其它rank也同样会做这么多的forward。

其次我们分析一下第一个公式，由这个对称性其实就可以知道，它是由forward和backward共同产生的。其实这个原因跟1F1B很相似，就是因为最开始forward过程，第一个rank先开始，所以后续rank会空转，那么相对于其它rank，rank0就会多处理 $(\text{pp\_degree} - \text{pp\_stage} - 1)$ 个数据，而backward也同样如此。所以在这里读者估计会和我有一样的困惑，为什么1F1B不乘以2呢?

我们对比一下1F1B和VPP,首先从全局视角来看，最早能出现backward的时间步位置在(假设forward和backward的时间相同)：

(pp\_degree-pp\_stage-1)*2+2

这里也比较容易理解，第一个micro_batch传到从当前stage传到最后一个stage的过程中，当前stage会产生 $(pp\_degree-pp\_stage-1)$ 个时间步，而当第一个micro_batch的backward从最后一个stage传到当前stage，当前stage又会产生 $(pp\_degree-pp\_stage-1)$ 个时间步，而最后一个stage做一个forward加一个backward，当前stage会产生2个时间步，所以最终得到上面的式子。

这个公式说明了什么？

说明在warm_up阶段，每个stage最多可以安排 $(pp\_degree-pp\_stage-1)*2+1$ 个时间步的操作，即，即使不按传统的1F1B或VPP来安排warm_up的时间步，也不会影响流水线正常进行，即整个时间不会增加也不会减少。可以从如下图看出：

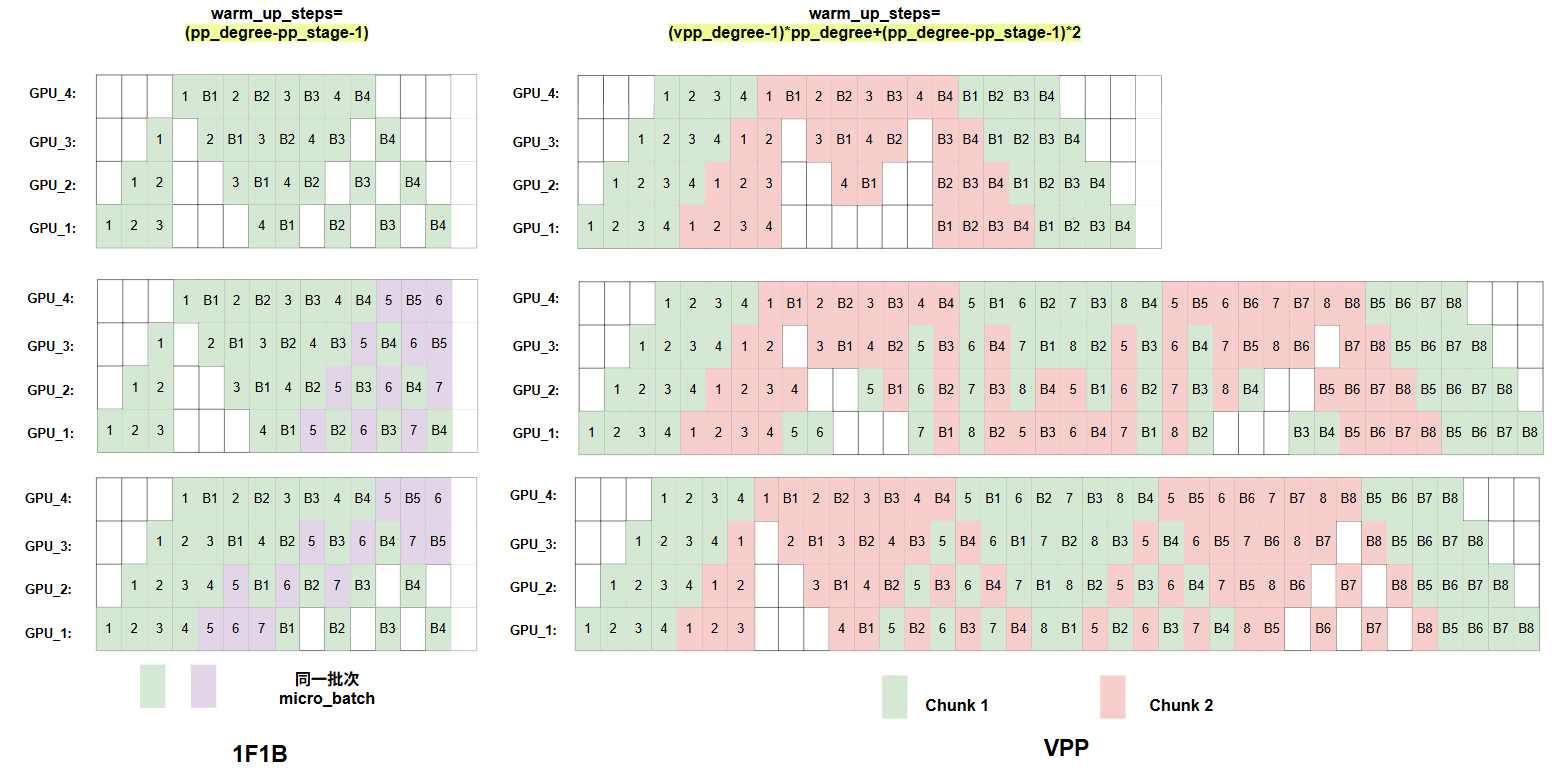
先看左边1F1B的图，左上角第一个是pp_degree=4，micro_batch=4的流水并行图，紧接着我们插入新的micro_batch，为了严格遵守warm_up_step=(pp_degree-pp_stage-1)，所以我们新的micro_batch选择插空填在后面，而紧接着下面一幅图，我们不遵守warm_up_step，直接插空填新的micro_batch。可以发现，因为最后一个rank始终是紧密排列的，所以总的PP并行的时间其实二者没有区别。但是我们会发现，两种方法，前者的显存峰值，要低于后者，因为前者将更多的micro_batch安排在1F1B过程进行，则每次都会释放一个activation值，这样可以降低峰值显存。所以其实1F1B也可以warm_up_step=(pp_degree-pp_stage-1)*2，但是并不减少时间，还会增大显存峰值，因此没有必要。

再看右边的VPP的图，第一幅图是标准的pp_degree=4，micro_batch=4的流水并行图。紧接着我们插入新的micro_batch，同样严格遵守warm_up_step=(pp_degree-pp_stage-1)*2+(vpp_degree-1)*pp_degree(此时pp_degree=8，micro_batch=4)，而我们可以联想到，既然1F1B可以把warm_up_step控制在(pp_degree-pp_stage-1)，那除去(vpp_degree-1)*pp_degree表示当前GPU上前几个chunk必须要经过的时间步，我们是不是同样可以不乘以2，让warm_up_step最小呢，即等于(pp_degree-pp_stage-1)，考虑到这一点，我就对原来的pp_degree=8，micro_batch=4进行了重排，可以发现，这时候总时间仍然没变，但是可以相对减少GPU的显存峰值，当然，二者只是一个二倍的关系，并且只与设备数有关，所以优化不是特别明显，但这个工作证明了，VPP在最后一层的数量计算上，确实可以和1F1B对齐。

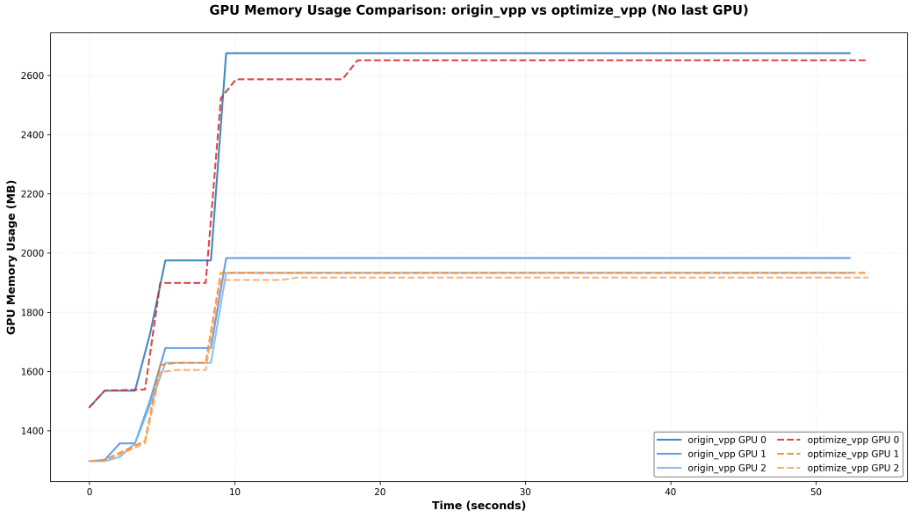
这里展示了4卡下的VPP，优化前后优化后，显存峰值，确实优化的不是很多，由于笔者机器有限，大家可以自行尝试，也许在像生产中96卡的情况下，还是能节省较大显存的。

VPP如何编排不同chunk(即vpp_stage)的forward和backward？

前面讲了如何去计算每个阶段的stage数，而有了stage数，对于VPP，由于每个GPU上存在不同的模型块，因此我们在编排的时候还需要知道，什么时候该编排哪一块，所以一般传统的VPP遵循的公式即：

\text{virtual\_pp\_stage} = \text{micro\_step} \mod ( \text{pp\_degree} \times \text{vpp\_degree} )

\text{virtual\_pp\_stage} = \left\lfloor \frac{\text{virtual\_pp\_stage}}{\text{pp\_degree}} \right\rfloor

这里的公式也比较好理解，首先 $\text{pp\_degree} \times \text{vpp\_degree}$ 求出来是一轮完整的forward或者bakcward经过的pp_stage数。而用micro_step求余，我们可以知道当前micro_batch在一轮中的哪个pp_stage上。我们注意当 $\text{num\_micro\_batch}=\text{pp\_degree}$ 的时候，则step最大值刚好等于一轮完整的pp_stage数，因为经过某一个GPU的micro_batch数为 $\text{vpp\_degree}*\text{micro\_batch}$ ，而一轮完整的forward或者backward经过的pp_stage数为 $\text{vpp\_degree}*\text{pp\_degree}$ ，所以此时step刚好等于一轮的pp_stage数，所以也可以看出，当micro_batch大于pp_stage数时，就会超过，因此这里用的求余操作。而知道在哪个pp_stage后，再用公式2即可得到其在当前GPU的哪一个模型块上（每个模型块编号都从0开始）。

1F1B和VPP都可能出现的死锁问题!

注意看，对于最后两个pp_rank来说，存在一个现象即GPU3做完forward给GPU4发送计算的activation值，而GPU4做完了B1向GPU3发送backward的grad值，此时GPU3等待GPU4接收到数据，再做下一个计算，而GPU4也在等待GPU3接收数据，再做接收GPU3传来的forward的数据做下一个计算，此时就会造成通信死锁。因此需要对send，recv通信和forward，backward计算做一个解耦，如下所示：

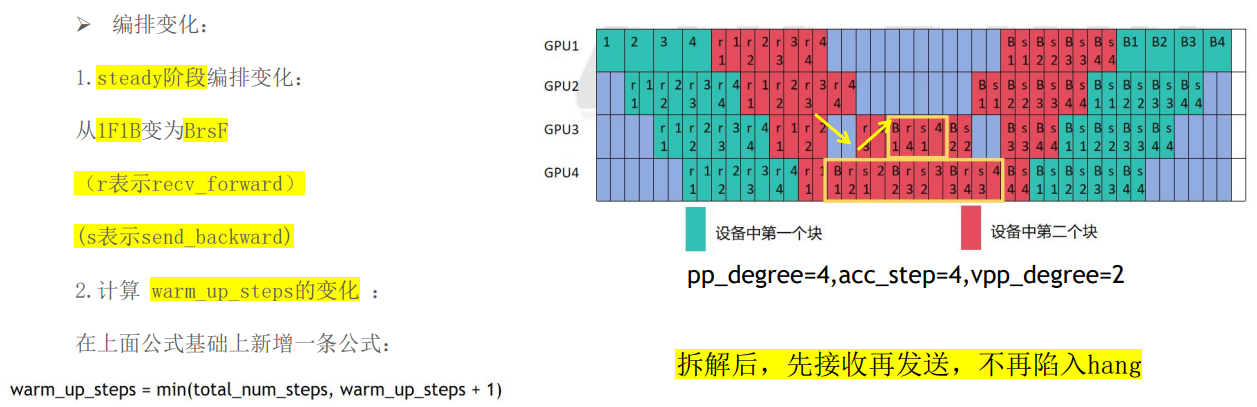
将forward操作拆解为recv_forward和forward(注意这里只拆了recv_forward，没有拆send_forward)，将backawrd拆解为backward和send_backward(只拆了send_backward，没拆recv_backward)，这样在1F1B阶段，始终保持先recv_forwrad再send_backwrad的顺序，即可解决死锁问题。

Zero Bubble

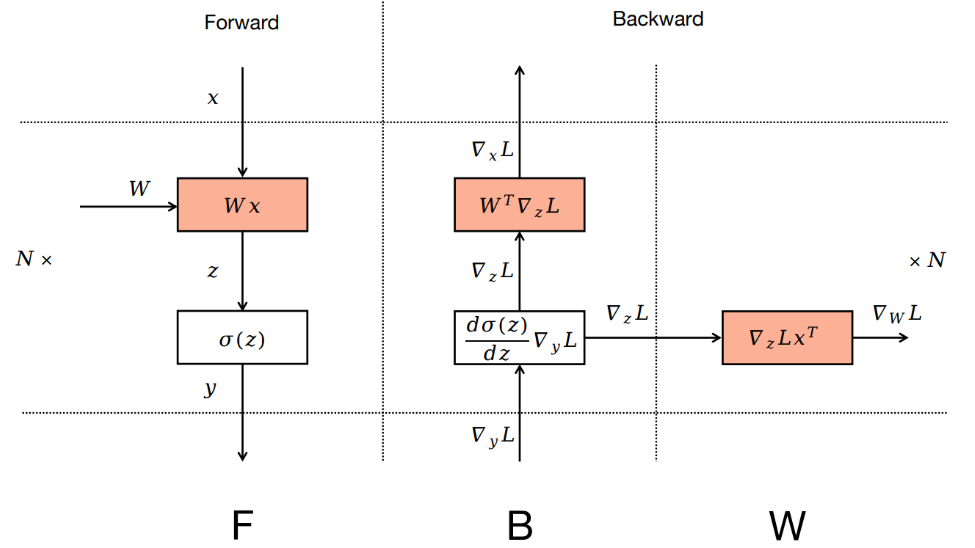
首先Zero Bubble的第一个优化点，就是将backward过程拆解成两个阶段，一个是对weight求导，一个是对输入input求导，我们需要注意，在backward的求导过程中，我们对weight和input求导，需要获取到链式法则传递下来的导数，▽L/▽Z，而这个就是当前层输出的导数(也就是下一层的输入的导数)，而有了这个导数就可以对weight和input求导。而当我们对input求导完成后，即使weight没有求导，仍然可以计算传递链式导数，到下一层求导，weight是否求导完成仅仅影响最后梯度的更新，因此我们可以将backward拆解，仅仅保证对输入input求导有序进行，并在这之间插入对weight的求导即可。（注意当前层weight的求导在插入时，需要保证上一层的input求导已经完成。）

1F1B

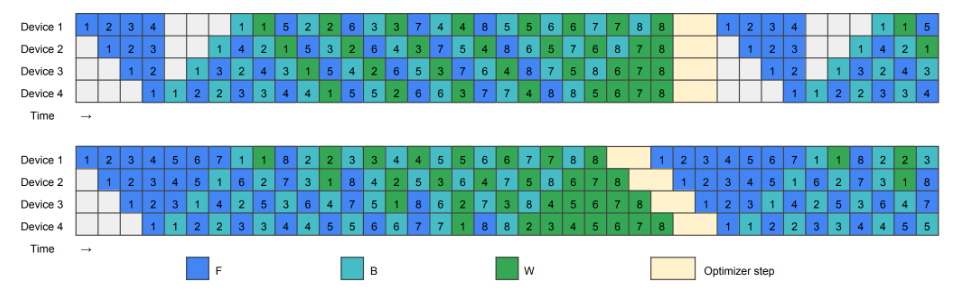
Zero Bubble

Zero Bubble也是在1F1B的基础上进行改进，分为两种，这里以ZB-H1和ZB-H2来讲解。首先ZB-H1是保证显存峰值不超过1F1B来编排的，可以看到，相比于1F1B来说，整个时间降低到了原来的1/3。而ZB-H2是显存峰值超过1F1B的情况进行编排，这样能在流水并行的过程中首先零bubble，但是注意这里移除了优化器步骤之间的同步。

在传统的PP实践中，为了数值稳健性，通常会在优化器步骤执行的管道阶段加上同步，例如需要计算全局梯度范数进行梯度裁剪、或者混合精度中执行NAN和INF值得全局检查，这两者都要跨所有阶段进行全局规约。因此论文移除优化器步骤需要考虑这个问题，于是提出了后验证的方式。

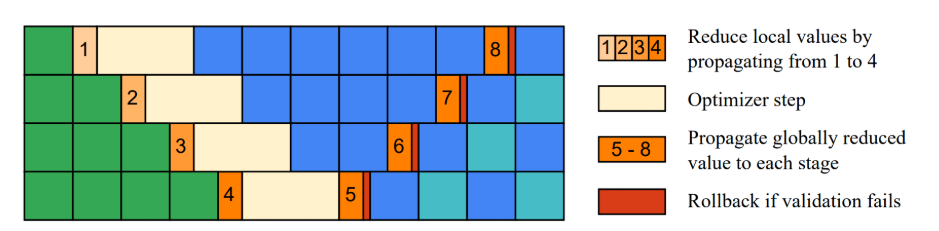
如图，逐个rank可以一次从前一个阶段接收到一个部分规约的局部信息，和当前局部状态融合，传递到下一个阶段，而当发现NAN或部分归约梯度范数超过裁剪阈值时，跳过更新。在下一次迭代的warmup阶段，完全规约的全局状态从最后一个阶段传播回第一个阶段，这时候每个阶段都有了全局状态，并以此来验证前一个优化器是否合法。如果不合法，则回滚，根据完全规约的全局状态，重新执行优化器步骤。

优化器回滚

当回滚优化器的时候，一种方法是保存全部的历史版本的参数和优化器抓鬼太，并在需要时恢复，但这种方法在内存上效率低下。因此论文针对AdamW优化器提出了回滚方法，因为优化器的更新公式，是可以逆运算的，所以根据逆运算计算回之前的状态即可。

最佳调度方案

同事为了适应更多的场景，论文提出了一种可自动搜索最佳调度方案的算法，一种启发式策略，可以在为批次足够大时生成接近最优解。

启发式算法有以下步骤：

热身阶段： 在内存允许的情况下，尽可能安排更多的 F，以减少第一个 B 前的等待时间。如果内存还有余量，可以安排额外的 F，但可能会延迟后续的 B。
稳定阶段： 在热身阶段后，我们交替安排 F 和 B。当有空闲时间超过 W 时，插入 W填充等待时间。即使等待时间不足 W，但当前等待时间会增加所有阶段中最大的等待时间时，我们也会插入 W。当内存接近饱和时，也会插入 W 释放一些内存(W需要activation的数据)。
阶段间调度： 确保每个阶段在用尽 F之前至少安排一个比下一个阶段更多的 F。当差异超过一定阈值时，考虑跳过某些阶段中的 F。
资源用尽： 在每个阶段，当 F 和 B 任务完成时，按顺序安排所有剩余的 W任务。

3.4 序列并行(SP)

Megatron提出的序列并行

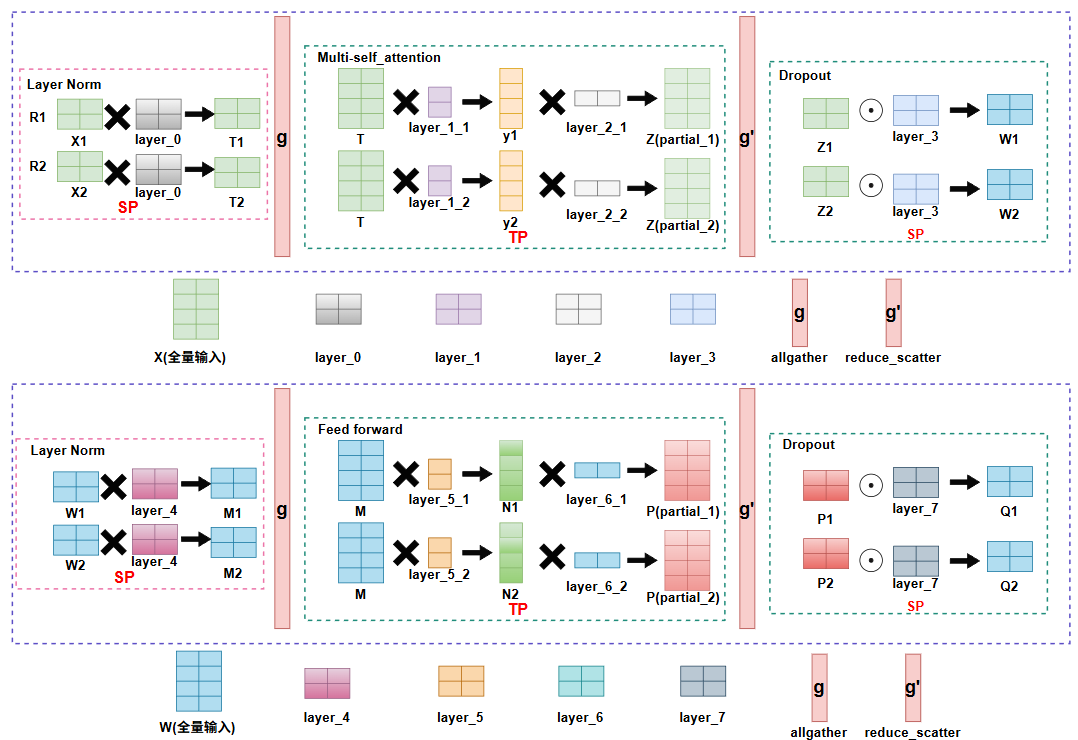
其实是结合了TP的特点，因为TP的RowParral输出时，需要调用all-reduce进行通信，将不同rank上的partial状态的输出给求和，所有rank得到全局输出，而all-reduce可以拆解为reduce_scatter和allgather。而引入SP后，我们可以发现，我们先做reduce_scatter，让每个rank得到全局输出的一部分，这样每个rank只需要计算部分数据的LayerNorm和Dropout，整个计算量被分摊到不同rank上，这样保存的在backward需要用到的activation数据也可以减少，从而减少每个rank的显存。而在进入如Multi-self_attention 和Feed Forward这种需要TP的层时，再调用all gather通信把SP层的数据收集起来，丢给TP层做计算。相当于把TP的通信拆分，这样整个过程SP+TP相比于TP通信量并没有变，并且还减少了显存的压力。

SP是对沿着seq_len，也就是序列维度进行切分，但是它切的层都在MLP层，即这些层，不同token之间是没有强关联性的。比如第一个token做归一化并不需要看第100个token的数据。

SP的提出主要是节省了MLP层的这些activation数据的显存，但是在计算超长序列时，multi-self_attention层在训练时仍然会需要N×N这么大的显存数据，N为序列长度，进一步能够解决超长序列文本的训练，CP被提出。

所以整个forward就需要2次reduce_scatter和allgather，再加上backward，通信量一共就是4次reduce_scatter和allgather。

注意为什么这里进入Feed forward前需要用allgather把数据合起来，原因是Feed forward这一层的参数被TP切分了，而每份参数都要和完整输入相乘。

通信与计算重叠(主要讨论Transfomer_Engine下的实现)

从上图可以看出SP+TP的组合，这里把原来TP的all-reduce通信拆分成了allgather+reduce_scatter，那么我们就分别讨论一下，allgather和reduce_scatter两部分如何做通信与计算的重叠。

allgather overlap(CommOverlapP2PBase::split_overlap_ag函数)

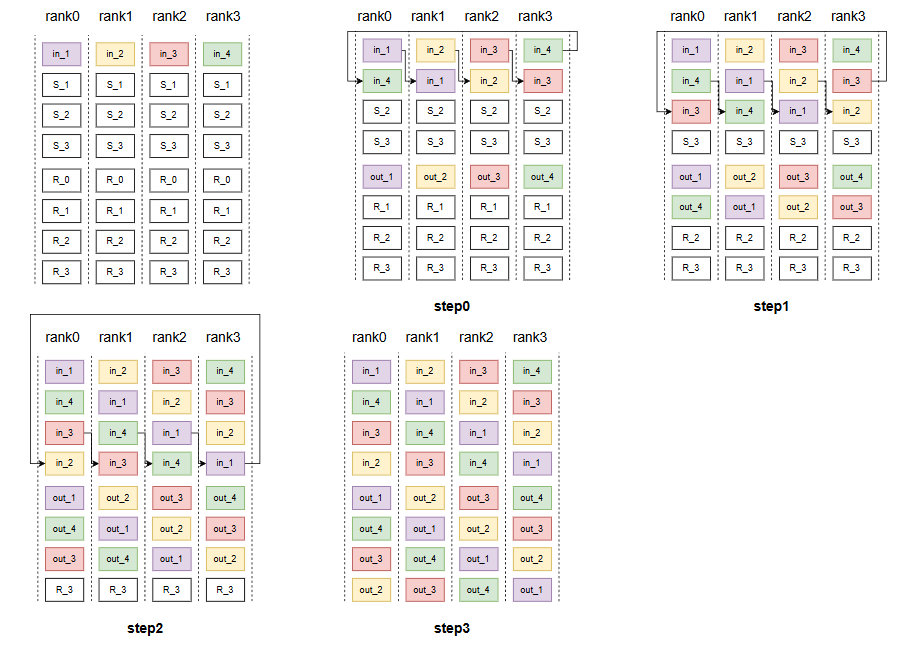
可以看到，这里计算和通信的overlap是采用的标准的Ring算法，即每个rank只会给相邻的rank发送数据，进行n-1轮发送和接收后，数据即传遍了所有的设备，并且每次发送和接收数据的同时，使用当前rank上一轮接受过的数据进行计算得到当前chunk的输出，最后一轮不再通信，只计算最后一块数据即可。下面的split_overlap_ag方法还实现了Aggregate Mode，将相邻两块GPU看作同一个rank，即先两两相邻的rank交换数据([0,1],[2,3]...)，接下来每2步跨度使用ring方法发送和接收数据，即rank0发送给rank2，rank1发送给rank3，接收也同样如此。这样做的好处是充分利用高带宽，以及减少通信次数。

void CommOverlapP2PBase::split_overlap_ag(const TensorWrapper &A, bool transa,
                                          const TensorWrapper &B, bool transb, TensorWrapper &D,
                                          TensorWrapper &bias, TensorWrapper &pre_gelu_out,
                                          TensorWrapper &workspace, bool grad, bool accumulate,
                                          bool use_split_accumulator, TensorWrapper &B_copy,
                                          cudaStream_t stream_main) {
  // ===== 第一部分：初始化和参数准备 =====
  int ori_sms = _ub_comm->sms;              // 保存原始 SM 数量，用于后续恢复，避免影响其他操作
  _ub_comm->use_ce = _use_ce;               // 设置是否使用 Collective Engine（NVIDIA 的硬件加速通信引擎）
  _ub_comm->sms = _num_comm_sm;             // 设置通信使用的 SM 数量，实现计算和通信的资源隔离
                                             // 通过限制通信使用的 SM，确保 GEMM 计算有足够的 SM 资源
  _ub_comm->cga_size = _cga_size;           // 设置 CGA (Cooperative Group Array) 大小，用于优化通信性能
  
  // 计算 GEMM 维度：根据 A 是否转置，动态确定矩阵维度
  // 矩阵乘法：D = A @ B，其中 A 的形状取决于 transa，B 的形状取决于 transb
  const size_t m = (transa) ? A.size(0) : A.size(1);  // 输出矩阵 D 的行数
                                                       // 如果 A 转置：A^T 的形状是 [k, m]，所以 m = A.size(0)
                                                       // 如果 A 不转置：A 的形状是 [m, k]，所以 m = A.size(1)
  const size_t k = (transa) ? A.size(1) : A.size(0);  // A 的列数 = B 的行数（用于矩阵乘法）
                                                       // 如果 A 转置：A^T 的列数是 A.size(1)
                                                       // 如果 A 不转置：A 的列数是 A.size(0)
  const size_t n_chunk = _ubufs[0].size(0);            // 每个 rank 持有的 B 的分块大小 = n / tp_size
                                                       // _ubufs[0] 是 userbuffer 的第一个 chunk，代表每个 rank 初始持有的 B 的一部分
                                                       // 在 Ring AllGather 过程中，每个 rank 会逐步收集所有 chunks，最终得到完整的 B

  // 计算通信和输出的分块大小
  const int comm_bytes = _ubufs[0].bytes();             // 每个分块的字节数
                                                       // 这是 userbuffer 中每个 chunk 的大小，用于计算内存偏移量
                                                       // 所有 chunks 大小相同，存储在连续的 _ubuf 缓冲区中
  const bool do_gelu = pre_gelu_out.numel() > 0;       // 是否需要 GELU 激活
                                                       // 如果 pre_gelu_out 不为空，说明需要保存 GELU 激活前的输出（用于反向传播）
  size_t workspace_size_chunk = workspace.numel() / _stream_compute.size();  // 每个计算流的工作空间大小
                                                       // 如果有多个计算流，需要将 workspace 平均分配给每个流，避免冲突

  // 验证 B_copy 缓冲区大小（用于反向传播时保存 AllGather 后的完整 B 矩阵）
  // 在反向传播时，需要完整的 B 矩阵来计算梯度，所以需要将 AllGather 后的 B 保存到 B_copy
  if (B_copy.numel() > 0) {
    NVTE_CHECK(B_copy.numel() == _ubuf.numel(), "Expected all-gathered B copy buffer with ",
               _ubuf.numel(), " elements but got ", B_copy.numel());
               // 检查 B_copy 的元素数量是否等于 _ubuf 的元素数量
               // _ubuf 存储了 AllGather 后的完整 B 矩阵，所以 B_copy 必须能容纳所有元素
    NVTE_CHECK(B_copy.element_size() == _ubuf.element_size(),
               "Expected all-gathered B copy buffer with ", _ubuf.element_size() * 8,
               "-bit data type but got ", B_copy.element_size() * 8, "-bit");
               // 检查 B_copy 的数据类型是否与 _ubuf 一致（例如都是 float16 或 bfloat16）
  }

  // ===== 第二部分：流同步初始化 =====
  // 在主流上记录起始事件，用于同步所有子流，确保所有流从同一时间点开始执行
  // 这是实现流水线重叠的关键：通过 Event 同步而非阻塞式同步，允许不同流并行执行
  NVTE_CHECK_CUDA(cudaEventRecord(_start_compute, stream_main));
  NVTE_CHECK_CUDA(cudaStreamWaitEvent(_stream_send[0], _start_compute, 0));  // 发送流等待主流
                                                                              // _stream_send[0] 用于发送数据到下一个 rank
  NVTE_CHECK_CUDA(cudaStreamWaitEvent(_stream_recv, _start_compute, 0));     // 接收流等待主流
                                                                              // _stream_recv 用于从上一个 rank 接收数据
  for (size_t i = 0; i < _stream_compute.size(); i++) {
    NVTE_CHECK_CUDA(cudaStreamWaitEvent(_stream_compute[i], _start_compute, 0));  // 所有计算流等待主流
                                                                                    // _stream_compute[i] 用于执行 GEMM 计算
                                                                                    // 可能有多个计算流，允许多个 GEMM 并行执行
  }
  
  // ===== 第三部分：聚合模式 (Aggregate Mode) =====
  // 当 _aggregate = true 时，使用 2X chunks 的聚合模式，减少通信轮数（从 tp_size 轮减少到 tp_size/2 轮）
  // 适用场景：当通信带宽充足但延迟较高时，聚合模式可以减少通信轮数，提高效率
  // 代价：每次通信的数据量翻倍（2X chunks），但总通信量不变
  if (_aggregate) {
    const int num_steps = _tp_size / 2;  // 聚合模式下只需 tp_size/2 步
                                          // 因为每次处理 2 个 chunks，所以轮数减半

    // 定义 2X chunks 的维度（每次处理 2 个分块，减少通信轮数但增加每次通信的数据量）
    std::vector<size_t> input_b_chunk_shape =
        (transb ? std::vector<size_t>{k, 2 * n_chunk} : std::vector<size_t>{2 * n_chunk, k});
        // 如果 B 转置：B^T 的形状是 [k, n]，所以每个 2X chunk 的形状是 [k, 2*n_chunk]
        // 如果 B 不转置：B 的形状是 [n, k]，所以每个 2X chunk 的形状是 [2*n_chunk, k]
    std::vector<size_t> output_chunk_shape = {2 * n_chunk, m};  // 输出 D 的 2X chunk 形状
    size_t input_b_chunk_size = 2 * n_chunk * k;   // 2X 输入分块大小（元素数量）
    size_t output_chunk_size = 2 * n_chunk * m;    // 2X 输出分块大小（元素数量）

    // 初始交换阶段：在相邻 rank 之间交换 1X chunk，为后续的 2X chunks 交换做准备
    // 目的：让每个 rank 都有 2X chunks 的数据，才能开始 2X chunks 的 Ring exchange
    int send_chunk_id = _tp_id;                     // 发送自己的 chunk ID（即当前 rank 的 ID）
                                                    // 每个 rank 初始持有自己的 chunk，需要发送给邻居
    int recv_chunk_id = (_tp_id % 2 == 0) ? _tp_id + 1 : _tp_id - 1;  // 接收相邻 chunk ID
                                                                      // 偶数 rank 接收 +1（例如 rank 0 接收 chunk 1）
                                                                      // 奇数 rank 接收 -1（例如 rank 1 接收 chunk 0）
                                                                      // 这样确保相邻 rank 配对交换
    // 计算内存偏移量：_ubuf 是一个连续的内存缓冲区，存储了所有 chunks
    // 每个 chunk 的大小是 comm_bytes，所以第 chunk_id 个 chunk 的起始位置就是 comm_bytes * chunk_id
    int send_offset = comm_bytes * send_chunk_id;   // 发送 chunk 在 _ubuf 中的字节偏移量
                                                    // 用于定位要发送的数据在缓冲区中的位置
                                                    // 例如：chunk 0 的偏移是 0，chunk 1 的偏移是 comm_bytes
    int recv_offset = comm_bytes * recv_chunk_id;   // 接收 chunk 在 _ubuf 中的字节偏移量
                                                    // 用于定位接收到的数据应该存储在缓冲区的哪个位置
                                                    // 这样确保每个 chunk 都存储在正确的位置，最终形成连续的 AllGather 结果
    int peer_rank = (_tp_id % 2 == 0) ? _next_rank : _prev_rank;  // 选择邻居 rank
                                                                   // 偶数 rank 与下一个 rank 交换（_next_rank）
                                                                   // 奇数 rank 与上一个 rank 交换（_prev_rank）

    // 执行初始的 1X chunk 交换：使用 userbuffers 进行点对点通信
    userbuffers_send(_ub_reg, send_offset, _ub_reg, send_offset, comm_bytes, _ub_comm, peer_rank,
                     _stream_send[0]);
                     // 参数说明：
                     // _ub_reg: userbuffer 注册 ID
                     // send_offset: 发送数据的源偏移量（在本地 _ubuf 中的位置）
                     // _ub_reg, send_offset: 发送数据的目标偏移量（在远程 rank 的 _ubuf 中的位置，这里使用相同偏移量）
                     // comm_bytes: 发送的字节数（1X chunk 的大小）
                     // peer_rank: 目标 rank
                     // _stream_send[0]: 使用的发送流
    userbuffers_recv(_ub_reg, recv_offset, _ub_reg, recv_offset, comm_bytes, _ub_comm, peer_rank,
                     _stream_recv);
                     // 参数说明：
                     // recv_offset: 接收数据的目标偏移量（在本地 _ubuf 中的位置）
                     // 其他参数与 send 类似，但方向相反

    // 等待接收完成，然后同步发送流和第一个计算流
    // 这是流水线的关键：确保数据已就绪，才能开始计算和下一轮通信
    NVTE_CHECK_CUDA(cudaEventRecord(_stop_recv, _stream_recv));  // 记录接收完成事件
    NVTE_CHECK_CUDA(cudaStreamWaitEvent(_stream_send[0], _stop_recv, 0));  // 发送流等待接收完成
                                                                             // 确保缓冲区可用，避免数据竞争
    NVTE_CHECK_CUDA(cudaStreamWaitEvent(_stream_compute[0], _stop_recv, 0));  // 第一个计算流等待接收完成
                                                                               // 确保输入数据已就绪，才能开始 GEMM 计算

    // Ring Exchange 阶段：计算本地 rank 在 2X chunks 模式下的起始位置和邻居 rank
    int local_rank_round2 = (_tp_id % 2 == 0) ? _tp_id : _tp_id - 1;  // 对齐到偶数位置
                                                                       // 偶数 rank 保持不变，奇数 rank 减 1
                                                                       // 这样确保所有 rank 从偶数位置开始 2X chunks 的交换
    const int next_rank = (_tp_size + _tp_id + 2) % _tp_size + _rank_round_tp;  // 下一个 rank（步长为 2）
                                                                                 // 例如：rank 0 -> rank 2 -> rank 0（环形）
                                                                                 // _rank_round_tp 确保在同一 tensor parallel group 内
    const int prev_rank = (_tp_size + _tp_id - 2) % _tp_size + _rank_round_tp;    // 上一个 rank（步长为 2）
                                                                                    // 例如：rank 2 -> rank 0 -> rank 2（环形）

    // Ring exchange 循环：每次处理 2X chunks，总共 num_steps 轮
    for (int i = 0; i < num_steps; i++) {
      // 计算当前迭代要发送和接收的 chunk ID（步长为 2）
      // 这些 chunk ID 决定了在 Ring exchange 过程中，每个 rank 处理哪些 chunks
      send_chunk_id = (_tp_size + local_rank_round2 - i * 2) % _tp_size;
                      // 发送的 chunk ID：从 local_rank_round2 开始，每次减 2，模 tp_size 确保在有效范围内
                      // 例如：rank 0, i=0 -> chunk 0; i=1 -> chunk (0-2) % 4 = chunk 2
      recv_chunk_id = (_tp_size + local_rank_round2 - i * 2 - 2) % _tp_size;
                      // 接收的 chunk ID：比发送的 chunk ID 小 2
                      // 例如：rank 0, i=0 -> chunk (0-2) % 4 = chunk 2; i=1 -> chunk (0-4) % 4 = chunk 0
      
      // 计算内存偏移量：根据 chunk ID 计算在 _ubuf 缓冲区中的字节偏移量
      send_offset = comm_bytes * send_chunk_id;   // 发送 chunk 的字节偏移量
                                                  // 用于定位要发送的 2X chunks 在缓冲区中的起始位置
      recv_offset = comm_bytes * recv_chunk_id;   // 接收 chunk 的字节偏移量
                                                  // 用于定位接收到的 2X chunks 应该存储在缓冲区的哪个位置
                                                  // 这样确保每个 chunk 都存储在正确的位置，最终形成连续的 AllGather 结果

      // GEMM 计算：使用当前可用的 2X chunks 进行矩阵乘法
      // 获取输入和输出的 tensor chunks，这些 chunks 指向 _ubuf 缓冲区中的相应位置
      auto input_b_chunk =
          get_buffer_chunk_like(B, input_b_chunk_size * send_chunk_id / 2, input_b_chunk_shape);
          // 获取 B 的 2X chunk：从 B 的起始位置偏移 input_b_chunk_size * (send_chunk_id / 2)
          // send_chunk_id / 2 是因为在 2X chunks 模式下，chunk ID 需要除以 2 来得到实际的 2X chunk 索引
          // 例如：send_chunk_id = 0 或 1 都对应第一个 2X chunk（索引 0）
      auto output_chunk =
          get_tensor_chunk(D, output_chunk_size * send_chunk_id / 2, output_chunk_shape);
          // 获取 D 的 2X chunk：从 D 的起始位置偏移 output_chunk_size * (send_chunk_id / 2)
      auto aux_chunk = (do_gelu)
                           ? get_tensor_chunk(pre_gelu_out, output_chunk_size * send_chunk_id / 2,
                                              {n_chunk * 2, k})
                           : TensorWrapper(nullptr, std::vector<size_t>{0}, pre_gelu_out.dtype());
          // 如果需要 GELU 激活，获取 pre_gelu_out 的 2X chunk（用于保存激活前的输出）
      auto workspace_chunk = get_tensor_chunk(
          workspace, (i % _stream_compute.size()) * workspace_size_chunk, {workspace_size_chunk});
          // 获取工作空间 chunk：根据迭代次数和计算流数量，轮询分配工作空间
          // 这样允许多个计算流并行执行，每个流使用不同的工作空间，避免冲突

      // 执行 GEMM：D[chunk] = A @ B[chunk] + bias（在独立的计算流上，与通信并行）
      // 这是流水线的核心：计算和通信同时进行，最大化 GPU 利用率
      nvte_cublas_gemm(A.data(), input_b_chunk.data(), output_chunk.data(), bias.data(),
                       aux_chunk.data(), transa, transb, grad, workspace_chunk.data(), accumulate,
                       use_split_accumulator, _math_sms,
                       _stream_compute[i % _stream_compute.size()]);
                       // 参数说明：
                       // A: 输入矩阵 A（所有 ranks 共享，不需要通信）
                       // input_b_chunk: B 的 2X chunk（从 _ubuf 缓冲区中获取，已通过 Ring exchange 收集）
                       // output_chunk: D 的 2X chunk（输出结果）
                       // bias: 偏置向量（可选）
                       // aux_chunk: GELU 激活前的输出（可选）
                       // transa, transb: 转置标志
                       // grad: 是否为反向传播
                       // workspace_chunk: 工作空间
                       // accumulate: 是否累加到输出
                       // use_split_accumulator: 是否使用分块累加器（提高数值精度）
                       // _math_sms: 用于 GEMM 的 SM 数量（排除通信使用的 SM）
                       // _stream_compute[i % _stream_compute.size()]: 使用的计算流（轮询分配）

      // 通信阶段（如果不是最后一步）：发送 2X chunks 到下一个 rank，从上一个 rank 接收 2X chunks
      if (i < num_steps - 1) {
        userbuffers_send(_ub_reg, send_offset, _ub_reg, send_offset, comm_bytes * 2, _ub_comm,
                         next_rank, _stream_send[0]);
                         // 发送 2X chunks：comm_bytes * 2 表示 2 个 chunks 的大小
                         // send_offset 是发送数据的起始位置（在本地 _ubuf 中）
        userbuffers_recv(_ub_reg, recv_offset, _ub_reg, recv_offset, comm_bytes * 2, _ub_comm,
                         prev_rank, _stream_recv);
                         // 接收 2X chunks：recv_offset 是接收数据的目标位置（在本地 _ubuf 中）
        
        // 记录接收完成事件，用于同步下一次迭代
        NVTE_CHECK_CUDA(cudaEventRecord(_stop_recv, _stream_recv));
        NVTE_CHECK_CUDA(cudaStreamWaitEvent(_stream_send[0], _stop_recv, 0));  // 发送流等待接收完成
                                                                                 // 确保缓冲区可用，避免数据竞争
        NVTE_CHECK_CUDA(
            cudaStreamWaitEvent(_stream_compute[(i + 1) % _stream_compute.size()], _stop_recv, 0));  // 下一个计算流等待接收完成
                                                                                                       // 确保输入数据已就绪，才能开始下一次 GEMM 计算
      }
    }
  } else {
    // ===== 第四部分：标准 Ring 模式 =====
    // 当 _aggregate = false 时，使用标准的 Ring AllGather 模式，每轮处理 1X chunk，总共 tp_size 轮
    // 这是更常见的模式，每次通信的数据量较小，但通信轮数较多
    
    // 定义标准 1X chunks 的维度
    std::vector<size_t> input_b_chunk_shape =
        (transb ? std::vector<size_t>{k, n_chunk} : std::vector<size_t>{n_chunk, k});
        // 如果 B 转置：B^T 的形状是 [k, n]，所以每个 1X chunk 的形状是 [k, n_chunk]
        // 如果 B 不转置：B 的形状是 [n, k]，所以每个 1X chunk 的形状是 [n_chunk, k]
    std::vector<size_t> output_chunk_shape = {n_chunk, m};  // 输出 D 的 1X chunk 形状
    size_t input_b_chunk_size = n_chunk * k;    // 1X 输入分块大小（元素数量）
    size_t output_chunk_size = n_chunk * m;      // 1X 输出分块大小（元素数量）

    // Ring AllGather 主循环：总共需要 tp_size 轮，每轮处理一个 chunk
    // 算法原理：每个 rank 初始持有自己的 chunk，通过 Ring 拓扑逐步交换，最终每个 rank 都收集到所有 chunks
    for (int i = 0; i < _tp_size; i++) {
      // 计算当前迭代要处理的 chunk ID
      // send_chunk_id: 当前要发送的 chunk（也是当前要计算的 chunk）
      // recv_chunk_id: 当前要接收的 chunk（用于下一轮计算）
      // 通过 (tp_id - i) % tp_size 确保每个 rank 最终收集到所有 chunks，且顺序一致
      // 例如：rank 0 处理顺序是 chunk 0, 3, 2, 1；rank 1 处理顺序是 chunk 1, 0, 3, 2
      int send_chunk_id = (_tp_size + _tp_id - i) % _tp_size;
                      // 发送的 chunk ID：从 _tp_id 开始，每次减 1，模 tp_size 确保在有效范围内
                      // 例如：rank 0, i=0 -> chunk 0; i=1 -> chunk 3; i=2 -> chunk 2; i=3 -> chunk 1
      int recv_chunk_id = (_tp_size + _tp_id - i - 1) % _tp_size;
                      // 接收的 chunk ID：比发送的 chunk ID 小 1
                      // 例如：rank 0, i=0 -> chunk 3; i=1 -> chunk 2; i=2 -> chunk 1; i=3 -> chunk 0
      
      // 计算内存偏移量：根据 chunk ID 计算在 _ubuf 缓冲区中的字节偏移量
      // _ubuf 是一个连续的内存缓冲区，按照 chunk_id 顺序存储所有 chunks
      // 每个 chunk 的大小是 comm_bytes，所以第 chunk_id 个 chunk 的起始位置就是 comm_bytes * chunk_id
      int send_offset = comm_bytes * send_chunk_id;   // 发送 chunk 在 _ubuf 中的字节偏移量
                                                      // 用于定位要发送的数据在缓冲区中的位置
                                                      // 例如：chunk 0 的偏移是 0，chunk 1 的偏移是 comm_bytes，chunk 2 的偏移是 2*comm_bytes
                                                      // 这样确保每个 chunk 都存储在正确的位置，最终形成连续的 AllGather 结果
      int recv_offset = comm_bytes * recv_chunk_id;   // 接收 chunk 在 _ubuf 中的字节偏移量
                                                      // 用于定位接收到的数据应该存储在缓冲区的哪个位置
                                                      // 例如：接收 chunk 3 时，偏移是 3*comm_bytes
                                                      // 这样确保接收到的数据存储在正确的位置，与其他 chunks 形成连续的内存布局

      // GEMM 计算：使用当前可用的 B chunk 进行矩阵乘法
      // 获取输入和输出的 tensor chunks，这些 chunks 指向 _ubuf 缓冲区中的相应位置
      auto input_b_chunk =
          get_buffer_chunk_like(B, input_b_chunk_size * send_chunk_id, input_b_chunk_shape);
          // 获取 B 的 1X chunk：从 B 的起始位置偏移 input_b_chunk_size * send_chunk_id
          // 在 Ring exchange 过程中，_ubuf 缓冲区逐步收集所有 chunks，所以可以直接使用 send_chunk_id 作为索引
      auto output_chunk =
          get_tensor_chunk(D, output_chunk_size * send_chunk_id, output_chunk_shape);
          // 获取 D 的 1X chunk：从 D 的起始位置偏移 output_chunk_size * send_chunk_id
          // D 的输出也按照 chunk_id 顺序存储，与 B 的布局一致
      auto aux_chunk =
          (do_gelu)
              ? get_tensor_chunk(pre_gelu_out, output_chunk_size * send_chunk_id, {n_chunk, k})
              : TensorWrapper(nullptr, std::vector<size_t>{0}, pre_gelu_out.dtype());
          // 如果需要 GELU 激活，获取 pre_gelu_out 的 1X chunk（用于保存激活前的输出）
      auto workspace_chunk = get_tensor_chunk(
          workspace, (i % _stream_compute.size()) * workspace_size_chunk, {workspace_size_chunk});
          // 获取工作空间 chunk：根据迭代次数和计算流数量，轮询分配工作空间
          // 这样允许多个计算流并行执行，每个流使用不同的工作空间，避免冲突

      // 执行 GEMM 计算（在独立的计算流上，与通信并行）
      // 这是流水线的核心：第 i 轮计算 chunk i，同时接收 chunk i+1（流水线重叠）
      // 计算和通信完全重叠，最大化 GPU 利用率
      nvte_cublas_gemm(A.data(), input_b_chunk.data(), output_chunk.data(), bias.data(),
                       aux_chunk.data(), transa, transb, grad, workspace_chunk.data(), accumulate,
                       use_split_accumulator, _math_sms,
                       _stream_compute[i % _stream_compute.size()]);
                       // 参数说明：
                       // A: 输入矩阵 A（所有 ranks 共享，不需要通信）
                       // input_b_chunk: B 的 1X chunk（从 _ubuf 缓冲区中获取，已通过 Ring exchange 收集）
                       // output_chunk: D 的 1X chunk（输出结果）
                       // bias: 偏置向量（可选）
                       // aux_chunk: GELU 激活前的输出（可选）
                       // transa, transb: 转置标志
                       // grad: 是否为反向传播
                       // workspace_chunk: 工作空间
                       // accumulate: 是否累加到输出
                       // use_split_accumulator: 是否使用分块累加器（提高数值精度）
                       // _math_sms: 用于 GEMM 的 SM 数量（排除通信使用的 SM）
                       // _stream_compute[i % _stream_compute.size()]: 使用的计算流（轮询分配）

      // Ring 通信（如果不是最后一步）：发送当前 chunk 到下一个 rank，从上一个 rank 接收下一个要计算的 chunk
      if (i < _tp_size - 1) {
        userbuffers_send(_ub_reg, send_offset, _ub_reg, send_offset, comm_bytes, _ub_comm,
                         _next_rank, _stream_send[0]);
                         // 发送当前 chunk 到 Ring 拓扑中的下一个节点
                         // 参数说明：
                         // _ub_reg: userbuffer 注册 ID
                         // send_offset: 发送数据的源偏移量（在本地 _ubuf 中的位置）
                         // _ub_reg, send_offset: 发送数据的目标偏移量（在远程 rank 的 _ubuf 中的位置，使用相同偏移量确保连续布局）
                         // comm_bytes: 发送的字节数（1X chunk 的大小）
                         // _next_rank: 目标 rank（Ring 拓扑中的下一个节点）
                         // _stream_send[0]: 使用的发送流
        userbuffers_recv(_ub_reg, recv_offset, _ub_reg, recv_offset, comm_bytes, _ub_comm,
                         _prev_rank, _stream_recv);
                         // 从 Ring 拓扑中的上一个节点接收下一个要计算的 chunk
                         // 参数说明：
                         // recv_offset: 接收数据的目标偏移量（在本地 _ubuf 中的位置）
                         // _prev_rank: 源 rank（Ring 拓扑中的上一个节点）
                         // _stream_recv: 使用的接收流
                         // 接收到的数据存储在 recv_offset 位置，确保与其他 chunks 形成连续的内存布局
        
        // 记录接收完成事件
        NVTE_CHECK_CUDA(cudaEventRecord(_stop_recv, _stream_recv));
        NVTE_CHECK_CUDA(cudaStreamWaitEvent(_stream_send[0], _stop_recv, 0));  // 发送流等待接收完成
                                                                                 // 确保缓冲区可用，避免数据竞争
                                                                                 // 这是流水线的关键：通过 Event 同步而非阻塞式同步，允许不同流并行执行
        NVTE_CHECK_CUDA(
            cudaStreamWaitEvent(_stream_compute[(i + 1) % _stream_compute.size()], _stop_recv, 0));  // 下一个计算流等待接收完成
                                                                                                       // 确保输入数据已就绪，才能开始下一次 GEMM 计算
                                                                                                       // 这样实现计算和通信的流水线重叠：第 i 轮计算时，第 i+1 轮的数据正在接收
      }
    }
  }

  // ===== 第五部分：结果复制和同步 =====
  // 如果需要保存 AllGather 后的 B（用于反向传播），则复制到 B_copy
  // 在反向传播时，需要完整的 B 矩阵来计算梯度，所以需要将 AllGather 后的 B 保存到 B_copy
  if (B_copy.numel() > 0) {
    NVTE_CHECK_CUDA(cudaMemcpyAsync(B_copy.dptr(), _ubuf.dptr(), _ubuf.bytes(),
                                    cudaMemcpyDeviceToDevice, _stream_send[0]));
                                    // 从 _ubuf 复制到 B_copy：_ubuf 存储了 AllGather 后的完整 B 矩阵
                                    // 使用异步复制，在发送流上执行（因为发送流此时可能已经空闲）
  }

  // 恢复原始 SM 设置，避免影响后续操作
  _ub_comm->sms = ori_sms;
  
  // 等待所有计算流完成：使用 Event 同步而非 stream synchronization，减少阻塞
  // 这是性能优化的关键：Event 同步允许其他操作继续执行，而 stream synchronization 会阻塞整个线程
  for (size_t i = 0; i < _stream_compute.size(); i++) {
    NVTE_CHECK_CUDA(cudaEventRecord(_stop_compute, _stream_compute[i]));  // 记录每个计算流的完成事件
    NVTE_CHECK_CUDA(cudaStreamWaitEvent(stream_main, _stop_compute, 0));  // 主流等待计算流完成
                                                                           // 这样确保所有 GEMM 计算都完成后，函数才返回
  }
  
  // 等待发送流完成
  NVTE_CHECK_CUDA(cudaEventRecord(_stop_send, _stream_send[0]));  // 记录发送流的完成事件
  NVTE_CHECK_CUDA(cudaStreamWaitEvent(stream_main, _stop_send, 0));  // 主流等待发送流完成
                                                                      // 确保所有数据都已发送完成
  
  // 等待接收流完成
  NVTE_CHECK_CUDA(cudaEventRecord(_stop_recv, _stream_recv));  // 记录接收流的完成事件
  NVTE_CHECK_CUDA(cudaStreamWaitEvent(stream_main, _stop_recv, 0));  // 主流等待接收流完成
                                                                      // 确保所有数据都已接收完成
                                                                      // 最终确保所有流（计算、发送、接收）都完成后再返回，保证数据一致性
}  // CommOverlapP2PBase::split_overlap_ag

reduce_scatter(CommOverlapP2PBase::split_overlap_rs函数)

实际代码(P2P实现)

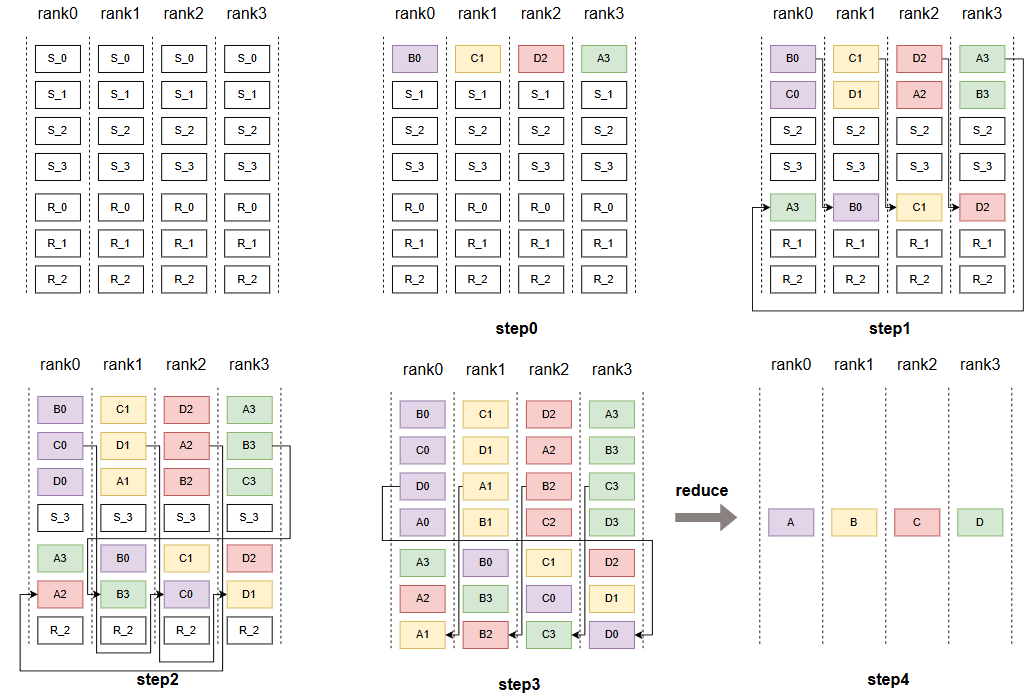
我们可以先看最原始的非overlap的图，在计算时，我们在多个tp_rank上会分别计算出一个大小相同但是是partial状态的输出，那么此时我们需要对它们做reduce，得到全局的输出，而又因为每张卡并不需要完整的全局输出，只需要自己负责的那一块数据，因此这里采用的是reduce_scatter，即使用ring结构，每个rank将接收的数据拼接自己已有的数据发送出去到下一个连续的rank上(首次发送rank_id块数据)。从而实现reduce_scatter。那么我们其实可以发现，既然每个rank并不需要全局的输出，是否我们可以先计算其它rank需要的那一块数据，发送给它，再发送的同时，再计算下一个rank需要的数据。（即对于n个rank来说，它需要发送(n-1)块数据给(n-1)个rank。）所以注意这里其实是P2P通信，不再是ring的通信

所以，4卡的reduce_scatter的overlap如图所示，每张卡会有4个发送缓冲区和3个接收缓冲区，为了实现显存的统一化管理减少内存碎片，这里7个缓冲区块放在一个连续的内存上。发送缓冲区块用于存放第i-1步计算出来的数据，而接收缓冲区用来存放第i步通信接收到的数据。

第0步，由于没有上一步计算的数据，因此不做通信

```cpp
/*
 * 函数名: CommOverlapP2PBase::split_overlap_rs
 * 功能: 使用 P2P（点对点）通信方式实现 ReduceScatter + GEMM 重叠计算
 * 
 * 参数说明:
 *   - A: 输入矩阵 A
 *   - transa: A 是否转置
 *   - B: 输入矩阵 B（已按 TP 分片）
 *   - transb: B 是否转置
 *   - D: GEMM 输出矩阵（同时也是通信缓冲区）
 *   - bias: 偏置向量（可选）
 *   - pre_gelu_out: GELU 前输出（可选，用于某些激活函数）
 *   - workspace: GEMM 工作空间
 *   - grad: 是否为梯度计算
 *   - accumulate: 是否累加到输出
 *   - use_split_accumulator: 是否使用分片累加器
 *   - rs_output: ReduceScatter 最终输出
 *   - stream_main: 主 CUDA 流
 */
void CommOverlapP2PBase::split_overlap_rs(
    const TensorWrapper &A, bool transa,
    const TensorWrapper &B, bool transb, TensorWrapper &D,
    TensorWrapper &bias, TensorWrapper &pre_gelu_out,
    TensorWrapper &workspace, bool grad, bool accumulate,
    bool use_split_accumulator, TensorWrapper &rs_output,
    cudaStream_t stream_main) {
  
  // ========== 第一部分：保存并配置通信器参数 ==========
  // 保存原始 SM（流式多处理器）数量，以便后续恢复
  int ori_sms = _ub_comm->sms;
  
  // 配置通信器参数
  _ub_comm->use_ce = _use_ce;           // 是否使用 CUDA Events
  _ub_comm->sms = _num_comm_sm;          // 为通信分配 SM 数量
  _ub_comm->cga_size = _cga_size;         // CGA（Cooperative Group Array）大小

  // ========== 第二部分：计算 GEMM 和通信的维度信息 ==========
  // 根据转置标志计算矩阵维度
  // m: 输出矩阵的行数（或列数，取决于转置）
  // k: 输入矩阵的共享维度
  size_t m = transa ? A.size(0) : A.size(1);
  size_t k = transa ? A.size(1) : A.size(0);
  
  // n_chunk: 每个 TP rank 处理的 B 矩阵 chunk 大小
  // 在 TP 模式下，B 矩阵被分成 _tp_size 个 chunk，每个 rank 处理一个
  size_t n_chunk = _ubufs[0].size(0);
  
  // comm_bytes: 每次通信传输的字节数（一个 chunk 的大小）
  const int comm_bytes = _ubufs[0].bytes();

  // 计算各种 chunk 的大小
  size_t input_chunk_size = n_chunk * k;      // B 矩阵每个 chunk 的元素数
  size_t output_chunk_size = n_chunk * m;     // GEMM 输出每个 chunk 的元素数
  size_t workspace_size_chunk = workspace.numel() / _stream_compute.size();  // 工作空间每个 chunk 大小

  // ========== 第三部分：同步主流和计算/通信流 ==========
  // 在主流上记录一个事件，确保所有后续操作都在主流的当前状态之后执行
  NVTE_CHECK_CUDA(cudaEventRecord(_start_compute, stream_main));
  
  // 让所有发送流等待主流的同步点
  for (size_t i = 0; i < _stream_send.size(); i++) {
    NVTE_CHECK_CUDA(cudaStreamWaitEvent(_stream_send[i], _start_compute, 0));
  }
  
  // 让接收流等待主流的同步点
  NVTE_CHECK_CUDA(cudaStreamWaitEvent(_stream_recv, _start_compute, 0));
  
  // 让所有计算流等待主流的同步点
  for (size_t i = 0; i < _stream_compute.size(); i++) {
    NVTE_CHECK_CUDA(cudaStreamWaitEvent(_stream_compute[i], _start_compute, 0));
  }

  // ========== 第四部分：流水线执行 GEMM 和 P2P 通信 ==========
  // 循环处理 _tp_size 个 chunk
  // 每个 rank 需要计算所有其他 rank 的 B chunk 与 A 的 GEMM 结果
  for (int i = 0; i < _tp_size; i++) {
    
    // --- 4.1 准备 GEMM 计算 ---
    // stream_id: 选择使用哪个计算流（轮询使用多个流以实现更好的并行度）
    int stream_id = i % _stream_compute.size();
    
    // input_b_chunk_id: 计算当前需要处理的 B chunk 的 ID
    // 公式: (_tp_id + i + 1) % _tp_size
    // 解释: 
    //   - _tp_id 是当前 rank 在 TP group 中的 ID (0 到 _tp_size-1)
    //   - +1 是因为第一个 chunk (i=0) 使用当前 rank 自己的 B chunk
    //   - 后续 chunk 依次使用下一个 rank 的 B chunk（通过 ring exchange 获得）
    //   - % _tp_size 确保索引在有效范围内
    int input_b_chunk_id = (_tp_id + i + 1) % _tp_size;

    // 获取对应的 B chunk 和输出 chunk
    auto input_b_chunk = get_tensor_chunk(B, input_b_chunk_id * input_chunk_size, {n_chunk, k});
    
    // 【关键】output_chunk 的数据指针被重定向到 _ubufs[i] 缓冲区
    // get_buffer_chunk_by_id 函数会：
    //   1. 先创建一个基于 D tensor 的 chunk（保留 D 的元数据，如 scale、dtype 等）
    //   2. 然后通过 set_rowwise_data(_ubufs[i].dptr(), ...) 将数据指针重定向到 _ubufs[i]
    //   3. 这样，output_chunk.data() 返回的指针就指向 _ubufs[i] 缓冲区
    //   4. GEMM 计算时，结果会**直接写入** _ubufs[i] 缓冲区，无需额外拷贝（零拷贝设计）
    auto output_chunk = get_buffer_chunk_by_id(D, i);  // 输出存储在 _ubufs[i] 中

    // 获取对应的工作空间 chunk
    auto workspace_chunk =
        get_tensor_chunk(workspace, stream_id * workspace_size_chunk, {workspace_size_chunk});

    // --- 4.2 执行 GEMM 计算 ---
    // 计算: A * B[input_b_chunk_id] + bias
    // **关键**：结果直接写入 output_chunk.data() 指向的内存，即 _ubufs[i] 缓冲区
    // 这是通过 get_buffer_chunk_by_id 函数实现的指针重定向，实现了零拷贝
    nvte_cublas_gemm(A.data(), input_b_chunk.data(), output_chunk.data(), bias.data(),
                     pre_gelu_out.data(), transa, transb, grad, workspace_chunk.data(), accumulate,
                     use_split_accumulator, _math_sms, _stream_compute[stream_id]);

    // --- 4.3 P2P 通信（从第二个迭代开始，i > 0）---
    // 第一次迭代 (i=0) 不需要通信，因为此时还没有计算好的结果可以发送
    // 第一次迭代计算完成后，结果存储在 _ubufs[0] 中
    // 第二次迭代 (i=1) 时，才会发送第一次迭代的结果（i-1=0 的结果）
    if (i > 0) {
      // 选择上一个 chunk 使用的计算流
      int prev_stream_id = (i - 1) % _stream_compute.size();
      
      // 计算通信的偏移量
      // send_offset: 发送数据的起始位置（前一次迭代 i-1 的计算结果）
      // 例如：i=1 时，发送 i-1=0 的结果，即 _ubufs[0] 的内容
      int send_offset = comm_bytes * (i - 1);
      // recv_offset: 接收数据的起始位置（下一个 chunk 需要的数据）
      // 注意: recv_offset 在 _ubufs 的后半部分（索引 _tp_size 到 2*_tp_size-1）
      int recv_offset = comm_bytes * (i - 1 + _tp_size);
      
      // 计算通信的目标 rank
      // send_rank: 接收当前 rank 发送数据的 rank
      //   公式: (_tp_id + i) % _tp_size + _rank_round_tp
      //   解释: 
      //     - (_tp_id + i) % _tp_size: 在 TP group 内的相对 rank
      //     - + _rank_round_tp: 加上 TP group 的起始 rank（支持数据并行）
      //   例如: 如果 _tp_id=1, i=2, _tp_size=4, _rank_round_tp=0
      //         send_rank = (1+2)%4 + 0 = 3
      //         表示 rank 1 发送数据给 rank 3
      int send_rank = (_tp_id + i) % _tp_size + _rank_round_tp;
      
      // recv_rank: 从哪个 rank 接收数据
      //   公式: (_tp_size + _tp_id - i) % _tp_size + _rank_round_tp
      //   解释: 使用模运算确保索引正确，支持反向 ring
      //   例如: 如果 _tp_id=1, i=2, _tp_size=4, _rank_round_tp=0
      //         recv_rank = (4+1-2)%4 + 0 = 3
      //         表示 rank 1 从 rank 3 接收数据
      int recv_rank = (_tp_size + _tp_id - i) % _tp_size + _rank_round_tp;
      
      // 等待上一个 chunk 的 GEMM 计算完成
      NVTE_CHECK_CUDA(cudaEventRecord(_start_comm, _stream_compute[prev_stream_id]));
      NVTE_CHECK_CUDA(cudaStreamWaitEvent(_stream_send[prev_stream_id], _start_comm, 0));
      NVTE_CHECK_CUDA(cudaStreamWaitEvent(_stream_recv, _start_comm, 0));
      
      // 执行 P2P 通信
      // 
      // 【重要】为什么 userbuffers_send 需要 recv_offset 参数？
      //
      // userbuffers_send 函数签名：
      //   userbuffers_send(srchandler, srcoffset, dsthandler, dstoffset, bytes, comm, peer, stream)
      //   参数说明：
      //     - srchandler: 源缓冲区 handler（发送方的缓冲区）
      //     - srcoffset: 源缓冲区偏移（发送方从哪个位置读取数据）
      //     - dsthandler: 目标缓冲区 handler（接收方的缓冲区）
      //     - dstoffset: 目标缓冲区偏移（接收方将数据放在哪个位置）**这就是 recv_offset**
      //     - bytes: 传输的字节数
      //     - comm: 通信器
      //     - peer: 目标 rank
      //     - stream: CUDA 流
      //
      // recv_offset 的作用：
      //   - 告诉接收方（send_rank）数据应该放在它的缓冲区的哪个位置
      //   - 在 userbuffers_send 的实现中，会计算目标 rank 的缓冲区地址：
      //     dstptr = comm->peer_ptr[dsthandler][peerlocal] + dstoffset
      //   - 这样发送方就知道应该将数据写入接收方缓冲区的哪个偏移位置
      //
      // 为什么需要这个参数？
      //   - 在 P2P 通信中，发送方需要知道接收方的缓冲区布局
      //   - 接收方可能有多个缓冲区区域，需要指定数据放在哪里
      //   - 在这个场景中，recv_offset = comm_bytes * (i - 1 + _tp_size)
      //     表示数据应该放在接收方的接收缓冲区区域（_ubufs[_tp_size] 之后）
      //
      // 发送: 将前一次迭代 (i-1) 的计算结果发送给 send_rank
      //   - 从发送方的 send_offset 位置读取数据
      //   - 写入接收方的 recv_offset 位置
      userbuffers_send(_ub_reg, send_offset, _ub_reg, recv_offset, comm_bytes, _ub_comm, send_rank,
                       _stream_send[prev_stream_id]);
      // 接收: 从 recv_rank 接收数据（用于后续迭代或 reduce）
      //   - 从 recv_rank 的 send_offset 位置读取数据
      //   - 写入本地的 recv_offset 位置
      userbuffers_recv(_ub_reg, send_offset, _ub_reg, recv_offset, comm_bytes, _ub_comm, recv_rank,
                       _stream_recv);
    }
  }

  // ========== 第五部分：同步所有流到主流 ==========
  // 等待所有计算流完成
  for (size_t i = 0; i < _stream_compute.size(); i++) {
    NVTE_CHECK_CUDA(cudaEventRecord(_stop_compute, _stream_compute[i]));
    NVTE_CHECK_CUDA(cudaStreamWaitEvent(stream_main, _stop_compute, 0));
  }
  
  // 等待所有发送流完成
  for (size_t i = 0; i < _stream_compute.size(); i++) {
    NVTE_CHECK_CUDA(cudaEventRecord(_stop_send, _stream_send[i]));
    NVTE_CHECK_CUDA(cudaStreamWaitEvent(stream_main, _stop_send, 0));
  }
  
  // 等待接收流完成
  NVTE_CHECK_CUDA(cudaEventRecord(_stop_recv, _stream_recv));
  NVTE_CHECK_CUDA(cudaStreamWaitEvent(stream_main, _stop_recv, 0));

  // ========== 第六部分：Reduce 所有 chunk 的结果 ==========
  // 
  // 【重要】Reduce 范围是如何指定的？
  //
  // reduce 函数通过以下参数指定 reduce 的范围：
  //   1. inputs 指针：指向输入缓冲区的起始位置（这里是 _ubufs[_tp_size - 1]）
  //   2. num_inputs：要 reduce 的缓冲区数量（_tp_size）
  //   3. input_size：每个缓冲区的大小（_ubufs[0].numel()）
  //
  // 为什么从 _ubufs[_tp_size - 1] 开始？
  //   - 在通信过程中，_ubufs[0] 到 _ubufs[_tp_size-2] 都被发送出去了
  //   - 只有 _ubufs[_tp_size-1] 没有被发送出去，它保留的是"自己的"计算结果
  //   - 这个缓冲区不需要发送，因为它是最后一个迭代的结果
  //
  // 关键理解：
  //   - reduce 函数从 inputs 指针开始，**向后**（向高地址）读取 num_inputs 个缓冲区
  //   - 函数实现：loader.load(tid + num_aligned_elements_per_input * input_id, tot_input_size)
  //   - 这意味着从 inputs + input_id * input_size 位置读取数据
  //   - 如果 inputs = _ubufs[_tp_size-1]，那么会读取：
  //     * input_id=0: _ubufs[_tp_size-1] (自己的结果，不需要发送)
  //     * input_id=1: _ubufs[_tp_size] (接收缓冲区，包含从其他 rank 接收的数据)
  //     * input_id=2: _ubufs[_tp_size+1] (接收缓冲区)
  //     * ...
  //     * input_id=_tp_size-1: _ubufs[2*_tp_size-2] (最后一个接收缓冲区)
  //
  // 但是，接收缓冲区里存储的是什么数据？
  //   - 在通信过程中，每个 rank 发送自己的 GEMM 结果给其他 rank
  //   - 接收缓冲区可能存储的是从其他 rank 接收到的、需要 reduce 的数据
  //   - 或者，数据在通信过程中被重新排列，使得接收缓冲区包含了需要 reduce 的数据
  //
  // 实际上，更可能的情况是：
  //   - reduce 函数需要 reduce 所有 _tp_size 个 chunk 的结果
  //   - 每个 rank 计算了不同的 chunk，这些结果分布在不同的 rank 上
  //   - 通过通信，每个 rank 收集到了所有 chunk 的结果（部分在自己的缓冲区，部分在接收缓冲区）
  //   - reduce 函数从 _ubufs[_tp_size-1] 开始，读取所有需要 reduce 的数据
  //
  // 注意：这里的具体数据布局可能需要查看通信的具体实现来确认
  char *reduce_buf_ptr = reinterpret_cast<char *>(_ubufs[_tp_size - 1].dptr());
  char *rs_output_ptr = reinterpret_cast<char *>(rs_output.dptr());
  
  // 根据数据类型选择 reduce 函数
  if (_ubuf.element_size() == 1 && rs_output.element_size() == 2) {
    // FP8 输入，BF16 输出：需要类型转换和 scale 处理
    // 函数签名：reduce_fp8_in_bf16_out(void *inputs, void *output, float *scale, 
    //                                    int num_inputs, int input_size, ...)
    // - inputs: 指向连续内存区域的指针，包含 num_inputs 个 FP8 缓冲区
    // - output: 输出 BF16 缓冲区
    // - num_inputs: _tp_size（要 reduce 的缓冲区数量）
    // - input_size: _ubufs[0].numel()（每个缓冲区的大小）
    char *rs_output_ptr = reinterpret_cast<char *>(rs_output.dptr());
    TRANSFORMER_ENGINE_TYPE_SWITCH_FP8ONLY(
        D.dtype(), fp8_type,
        reduce_fp8_in_bf16_out<fp8_type>(reduce_buf_ptr, rs_output_ptr, D.scale_inv(), _tp_size,
                                         _ubufs[0].numel(), stream_main););
  } else {
    // BF16 输入输出：直接 reduce
    // 函数签名：reduce_bf16(void *inputs, void *output, int num_inputs, int input_size, ...)
    // - inputs: 指向连续内存区域的指针，包含 num_inputs 个 BF16 缓冲区
    // - output: 输出 BF16 缓冲区
    // - num_inputs: _tp_size（要 reduce 的缓冲区数量）
    // - input_size: _ubufs[0].numel()（每个缓冲区的大小）
    //
    // 在 CUDA kernel 中的实现逻辑：
    //   for (input_id = 0; input_id < num_inputs; ++input_id) {
    //     从 inputs + input_id * input_size 位置读取数据
    //     累加到 accum_buf
    //   }
    //   将累加结果写入 output
    reduce_bf16(reduce_buf_ptr, rs_output_ptr, _tp_size, _ubufs[0].numel(), stream_main);
  }

  // ========== 第七部分：恢复通信器参数 ==========
  _ub_comm->sms = ori_sms;
}
```

backward中的overlap(bulk overlap)

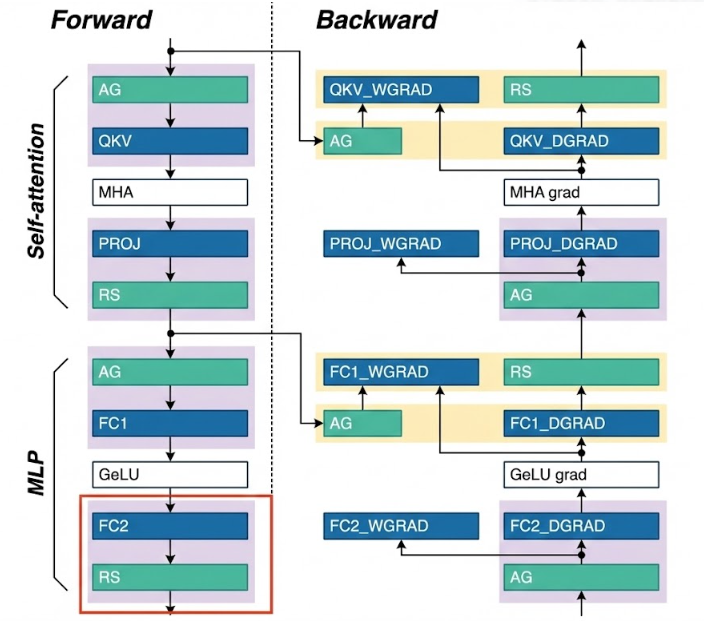
如图所示，在backward 的时候，黄色框中对应的部分也会做overlap——因为在forward的时候，每个rank经过Reduce_Scatter后，只保存了部分输出，而我们在计算FC1_WGRAD时，需要这一层的完整输入(因为forward是做了AG，将输入完整拼接起来，进一步做的MLP层的计算，因此此时计算FC1_WGRAD也需要做AG获得完整激活值)，而又因为计算FC1_DGRAD(即当前层输入的梯度)时，只需要当前层的weight和上一层传下来的梯度，并不需要完整的输入数据，因此此时的AG和FC1_DGRAD天然可以做并行。

3.5 上下文并行(CP)

目前提到比较多的是Colossal-AI的Ring Attention以及DeepSpeed的Ulysses。以及Megatron的cp(增强版的sp)。

Ulysess：切分Q、K、V序列维度，核心卖点保持通信复杂度低，和GPU数无关，和序列长度呈线性关系。

Ring-Attention：切分Q、K、V序列维度，核心卖点是通信和计算重叠。

DeepSpeed的Ulysses

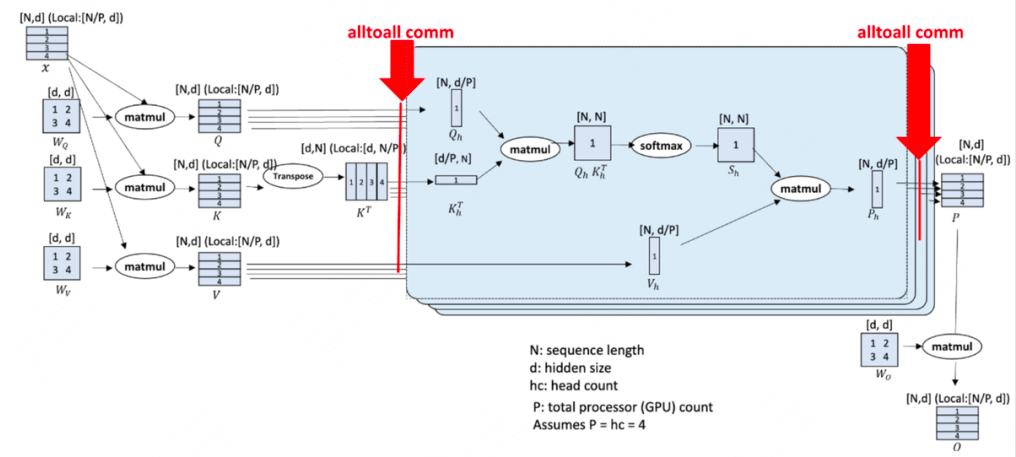
这个思想主要是将输入X在Sequence维度进行切分，切分后，此时Sequence维度是N/P，其中N表示序列长度，P表示Rank个数，而d表示hidden_dim。由于每个Rank上都保留了完整的d维度，因此可以直接和大矩阵WQ，WK，WV相乘，分别得到大小为(N/P,d)大小的分块Q,K,V，然而计算attention时，是需要Sequence维度保持一个完整状态，因为存在token之间的关联，所以这里使用一个alltoall的通信操作来把切分转到下一个维度，如果是attention就会转到头维度。如下图给了详细的解释：

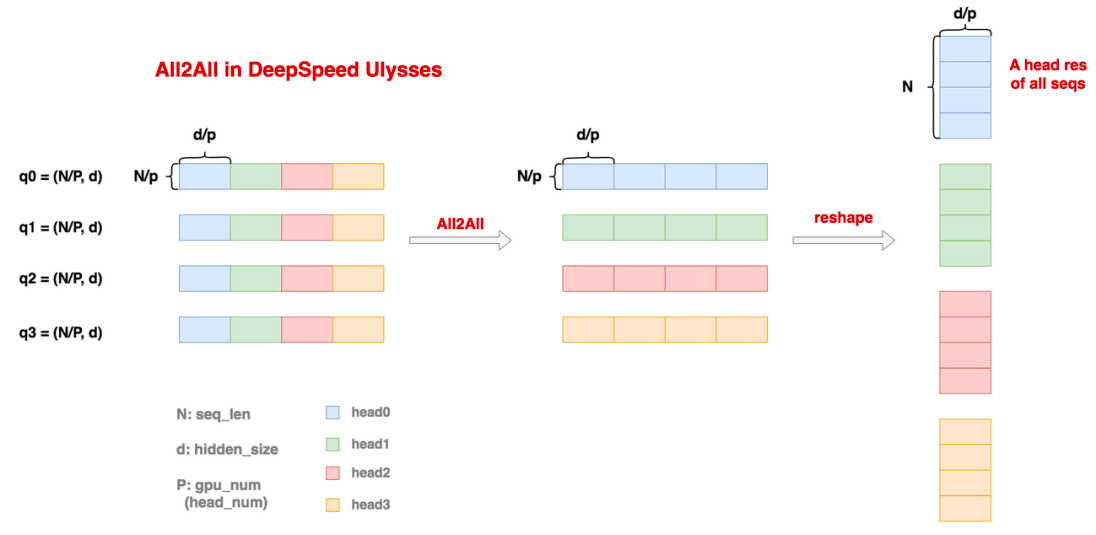
这里首先展示了4个rank上保存的输入，此时每个rank保存了完整的头维度，和N/P大小的sequence维度，当使用all2all时，每个rank根据自身rank号保留自己的那一块数据，然后把其它块分别发送给对应块号的rank，这样，此时每个rank都保存了完整的N个token的信息，做一个reshape操作，即可看到，每个rank的sequence是完整的，而头维度被切成了P分。所以这里其实还需要满足head_num是P的整数倍，每张卡其实是算1个/若干个head的结果，与TP非常相似。

所以这里也有一个重点，如果采用GQA，则不能用ulysses，因为此时KV head只有一对，无法切分，而上述方法是要对Q,K,V都做均匀切分。

Attention计算结束后，最后的输出score形状仍然是(N,d/p)，接下来，所有的rank再1次alltoall，注意这时候只有一个输出，所以是一次，而在输出的时候，因为Q,K,V分别有一份，所以输入是3次alltoall。最终每张卡上都恢复成(N/p,d)的形状，再和Wo矩阵相乘，得到(N/p,d)的结果。接着进入MLP层，由于MLP层本身就不涉及到token间的相关性计算，因此每个seq_chunk都可以独自计算。重复上述操作，直到计算到Loss为止。注意这里和Megatron中的TP+SP不一样，只需要在attention前后通信。因为每个rank最后loss都是部分数据算出来，所以应该还有梯度同步的过程，不过梯度同步的通信量可以和梯度计算过程overlap。

Megatron的TP+SP与Deepspeed的ulysses通信量对比分析：

Megatron的TP+SP包括forward和backward过程共4次(allgather+reducescatter)，也是8次，一次allgather的通信量大概是Nd，reducescatter也是如此，所以是8Nd。

ulysses的通信包括forward过程的4次alltoall，反向也如此。所以一共8次alltoall单卡的通讯量为(8Nd)/P,这也意味着，当N变大时，如果可以同倍数增加gpu的数量，那么就可以让单卡通讯两维持一个不变的数，不过要注意，这里的P的数量会被head_num限制住。

Colossal-AI的Ring Attention

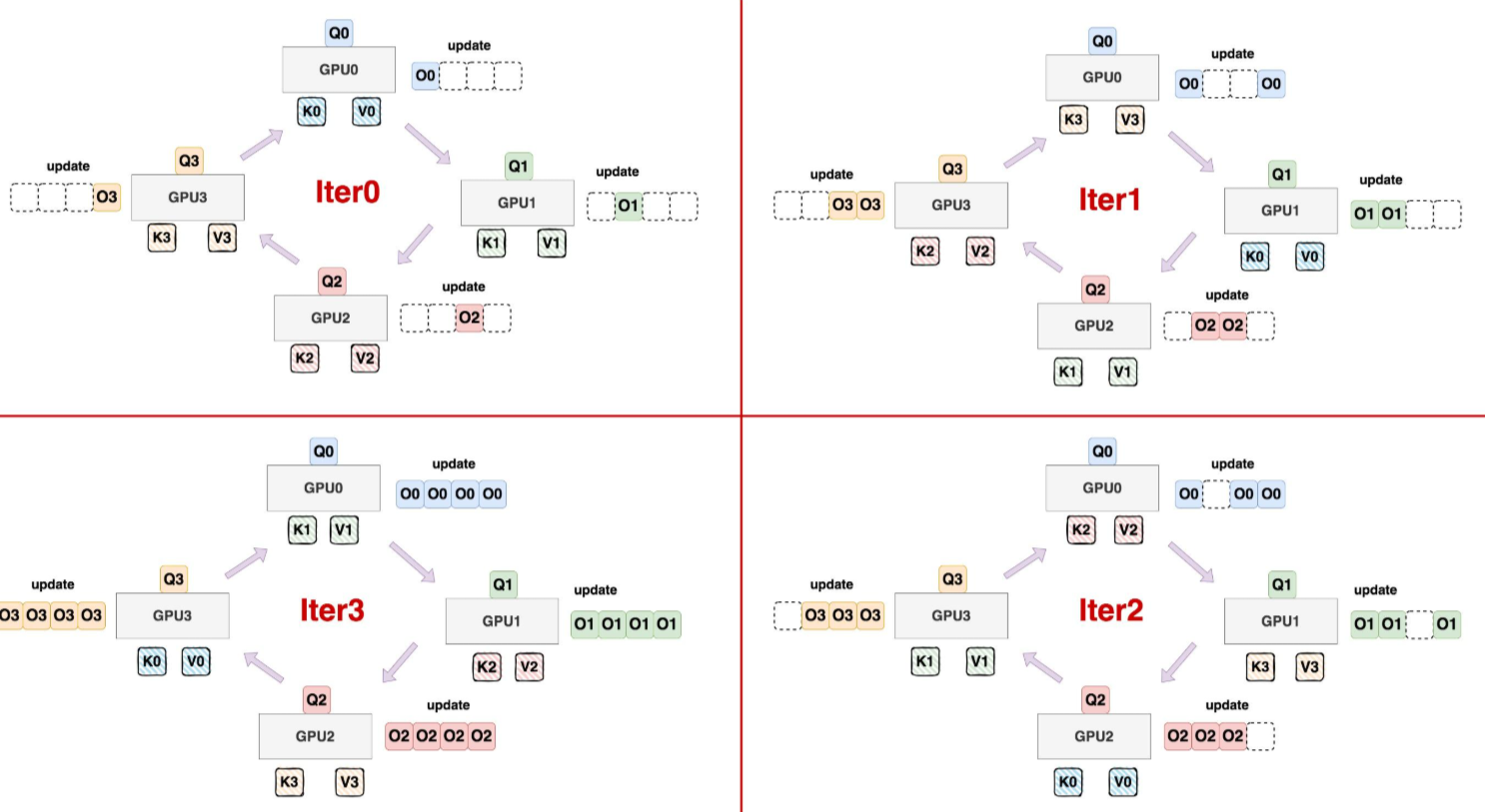
可以看到Ring Attention其实和FA V2很相似，都是在Sequence_lenth维度上做切分，但FA V2只在Q的Sequence_lenth维度做了切分，而Ring Attention做了进一步的切分，因为通过阅读FA V2的算法可以发现，其实每次用Q和KV计算得出来的 $O_i$ 其实是一个partial状态，最终就是在上一个partial状态的 $O_i$ 去更新计算下一个partial状态，每次只需要当前的max和sum的信息即可，逐步得到完整O的分块。而这个计算中，每个partial状态的顺序并不是严格，并且每个rank上都保存完整的K,V块，非常浪费显存。

基于此Ring Attention应运而生，它把Q,K,V都在Sequence_lenth维度做了切分，在实际计算时，通过ring的操作，每次计算完后，环形交换K,V对，这样经过(rank-1)轮循环后，所有rank上的O的那部分块都能完整更新。

最佳分块大小Chunk_size分析

假设硬件的算力上限是F：F表示这个硬件每秒最多能完成的浮点运算次数，单位是FLOP/S。

假设硬件的带宽上限是B：表示这个硬件每秒最多能完成的内存交换量，单位是Byte/s。

那么在单卡上对某个QKV chuck计算attention有， $Q*K^T=(C,d)*(d,C)$ ，所以attention score的计算量为 $2d^2c$ FLOPs(乘法+加法)，而 $Score*V=(C,C)*(C,d)$ ，所以计算量为 $2d^2c$ 。

而假设用bf16/fp16进行训练，则传输的KV数据量大小(单位bytes)为：

K chunk 大小为2dc bytes ，V chunk 大小为 2dC bytes

所以传输KC的数据量大小为4dC bytes

因为传输时间要小于计算时间，才能够把传输时间给覆盖掉，则有：

$\frac {4dC}{B}< \frac {4d^2C}{T}$

转化后有:

$C >= \frac {F}{B}$

这里还没有计算Q,K,V的计算时间，所以这个C是非常严格的，我们可以根据硬件的算力F和带宽上限B来得到最佳Chunk_size。

Ring Attention存在的问题

1.负载不均衡

我们可以假设我们用的是casual mask，那么这就意味着，每个token只关心和它和自己以及它之前的token的attention，而此时传统的ring attention设计是每个分块Q都会和所有的KV块做计算，这就会导致前面的一些Q块和KV块的计算完全是浪费的，实际也不会计算因为不需要，就会导致gpu空转，浪费资源。

2.与FA V2更新 $O_i$ 不同

前面介绍过FA V2在更新O的时候，是每次并不得到最终的softmax_lse，即只在最后和所有KV块计算的结果累积之后，再除以一个总的sum_l，来计算得到最终的输出O。

而ring attention为了保留每次计算后更高的精度，选择了每次计算出一个临时的全局O，即将除以一个总的sum_l，放在循环里面，每次计算得到当前的最大m和当前l的sum，并用这两个值得到一个最终的O，这样可以较大程度上保留更高的数值精度。

Megatron的cp

Megatron主要是在Ring Attention的基础上做了负载均衡：

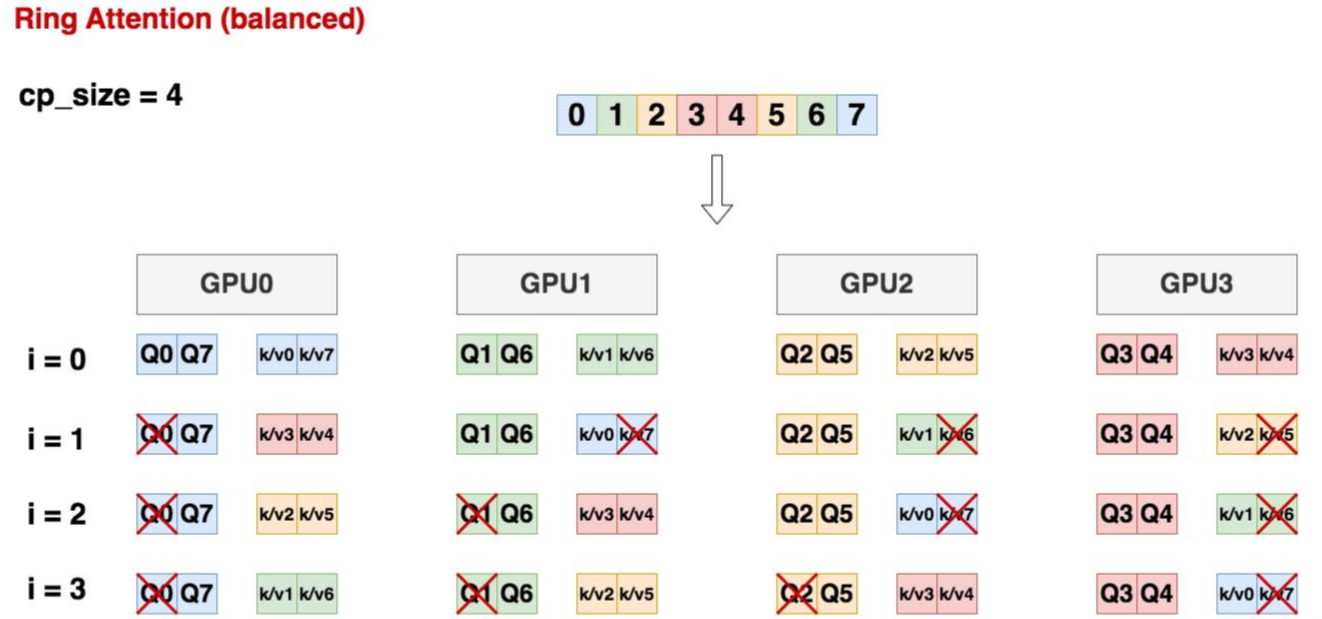
由于每个Q块的计算和KV块的计算并不需要严格按顺序，这个在ring attention中就证明过，这里不再赘述，那么其实可以不按顺序划分整个Q矩阵，而是将Q矩阵，前面的块后后面的块拼接起来，同样KV块也做一样的操作，这样就可以在计算量上做到负载均衡。

如上图所示，假设cp_size = 4，也就是我们打算在4块gpu上做ring attention。

首先，对于原始输入数据X，我们将其切分为2*cp_size = 8块，也就是上图的0～7 chunk

[0,7]，[1, 6]，[2, 5], [3, 4]分别组成4个seq_chunk，安放在gpu0~gpu3上。

则在ring attention下，每块gpu上计算cp_size次后，就能得到最终的output。例如对于gpu0，计算4次后，就能得到[0, 7]这两个位置最终的attention结果。

图中接着展示了在不同的iteration中，每块卡上的计算情况，可以发现：

i = 0时，每张卡上都是4个小方块在做attn计算

i = 1/2/3时，每张卡上都是3个小方块在做attn计算

总结来看，每个iteration中，各卡的计算量是相同的。不存在朴素ring attention上某些卡空转的情况。

同时注意到，当i = 1/2/3时，总有Q或者KV块不参与计算，如果我们用rank表示这是cp_group内的第几块gpu（例如rank=0就是上面cp_group中的第0块gpu），则对于某张卡，我们有如下规律：

其中：

用于分配哪张卡上应该维护哪些Q块的代码在：https://github.com/NVIDIA/Megatron-LM/blob/main/megatron/training/utils.py#L233

用于处理实际QKV计算时应该保留哪些数据块，去掉哪些数据块的代码在：https://github.com/NVIDIA/TransformerEngine/blob/main/transformer_engine/pytorch/attention/multi_head_attention.py

混合并行

注意Megatron的CP和SP是完全不同的两种并行策略，虽然都是沿着Sequence_len维度切分，但是SP是和TP共用，所以它们共用同一组rank，而CP则是完全独立的一组并行策略，和TP使用不同的rank组。

计算和通讯的overlap

在megatron cp中，共包含3个cuda流：

NCCL stream：定义在cp_group内，是用于做KV发送和接收的cuda流
**Stream0和Stream1：**都是用于做计算的cuda流，这两个流的作用是可以并行执行attn的计算和softmax_lse的更新。

megatron cp中，除了对计算和通信做并行，同时还对计算中的attention和softmax_lse更新做了并行。这里attention计算指的是FA V2算法中，不对softmax_attention结果除以sum_l的结果 $O_i$ ，而softmax_lse表示利用当前的局部sum_l对结果 $O_i$ 做修正

可以发现上述的attention和softmax_lse的计算对于同一组QKV来说是串行的，但是对不同组的QKV来说是可以并行的，但是要保证，更新softmax_lse要在下一次计算完最终的Attention之前完成，因为softmax_lse时负责修正 $O_i$ ，若 $O_i$ 被新计算的值覆盖，此时就会计算错误。

overlap图

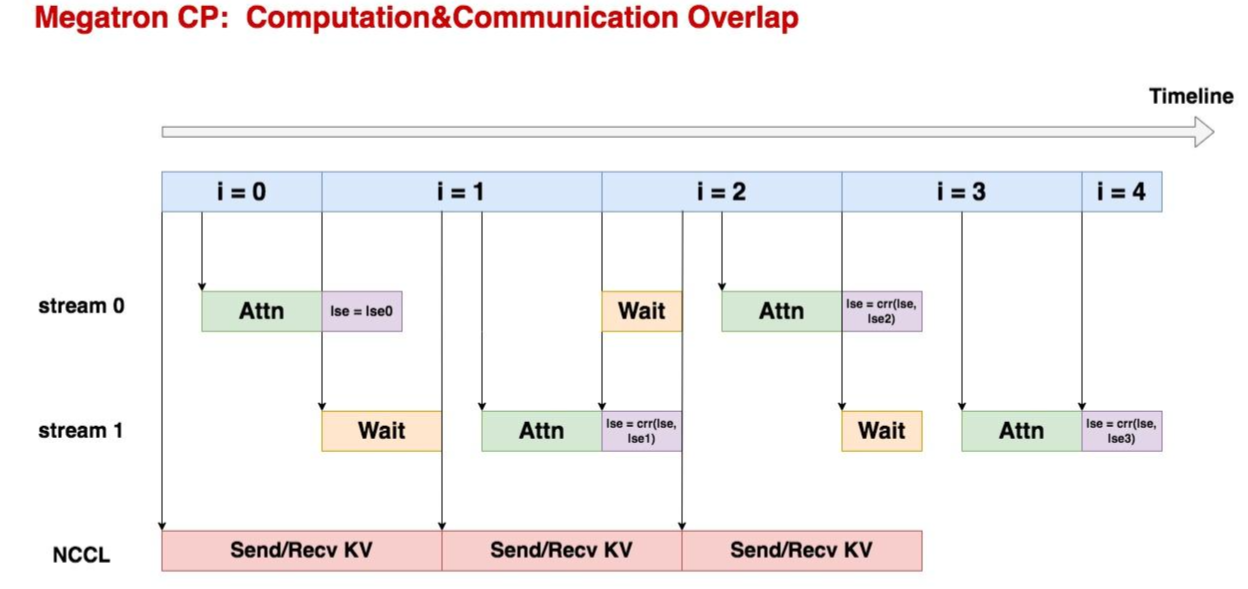
可以看到，cp_size = 4，i表示 $CP_i$ ，即CP每块计算的序号：

1.在初次计算时，即i=1时，不需要更新，因为此时只有一个sum，输出的 $O_i$ 无需修正

2.当i=1时，接收到KV时开始计算attention，stram0 赋值lse =lse0，不需要做lse的更新，同时stream1计算当前的attention。

3.当i=2时，stream1更新lse，而stream0则用来计算Attention。

3.6 专家并行(EP)

1.Gshard

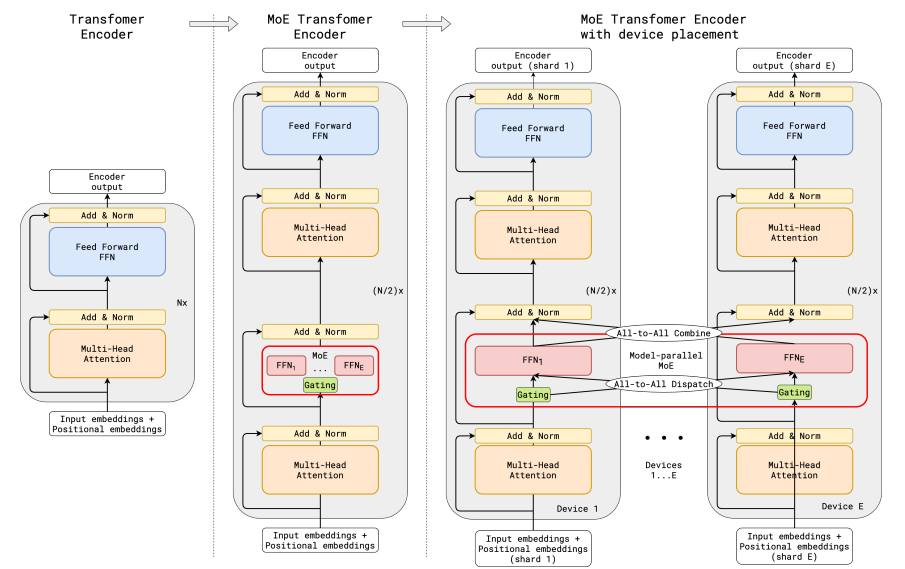
MOE的概念最早由Gshard论文引入，如图就是MOE的核心流程图，分别展示了单卡视角和多卡视角的MOE运作方式。主要的操作就是将原来的FFN的大矩阵，变成多个expert，所有token经过门控网络计算后，计算得出要发送到哪些专家，在Gshard中使用的是TOP2Expert，即每个token选择分数最高的两个专家，每个专家会处理自己分配到的token，并且输出一个结果，最终每个token的结果会根据token分到不同专家的概率和专家的结果做一个加权和，得到该token最终的输出。若在多卡上分配所有专家，则在发送token到不同专家和从不同专家汇总接收token处理后的结果时需要做All-to-All的通信。

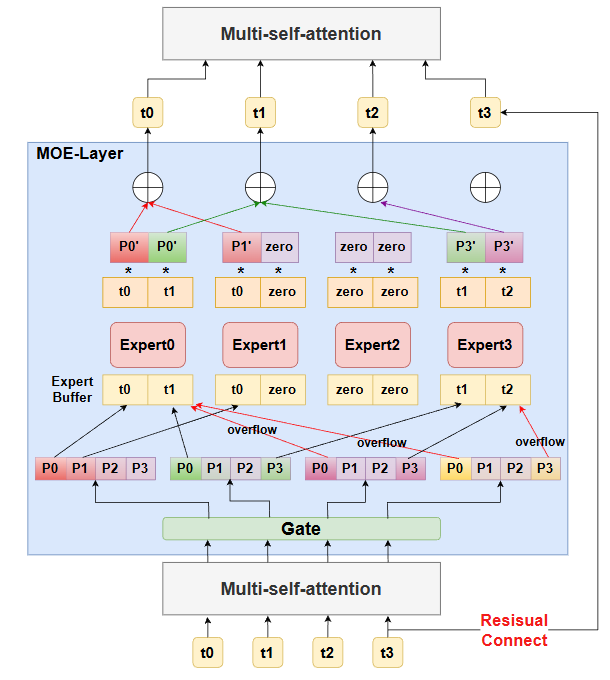
如图为单卡视角下的MOE-Layer的结构，注意MOE的输入为Multi-self-attention的输出，而MOE的输出为Multi-self-attention的输入，expert是从FFN层变换过来的，但是并不意味之是对FFN的均匀切分，expert的大小可以自定义，甚至可以大于原来的FFN，因为此时的expert不再和所有token做全量计算，而是仅仅和部分token做计算，即体现稀疏模型的结构

其中P0'表示token选中的专家的概率，再做归一化后的值，比如对于token0来说选中了expert1和expert2，则 $P0'=\frac{P0}{P0+P1}$

2.输入数据

首先注意所有tokens经过attention层处理后，大小为(batch_size,seq_len,M),其中M为token的embedding维度。在FFN层，我们会把batch_size和seq_len两个维度拍平，即将所有token融合，得到一个S，S即为该batch中所有token的数量，因此此时MOE层输入数据的尺寸为(S,M)。

3.Gate(门控网络)

门控网络也是一个线性层，用来判断每个token应该送往哪个expert，有时也被称为Router(路由)。Gate的尺寸大小为(M,E),其中E表示expert的数量，因此输入数据(S,M)经过处理后，得到prob数据(S,E)，即得到每个token对应的所有专家的权重，Gshard只关心概率最大的两个expert。图中使用最深的颜色表示最大概率的token，而用次深颜色表示第二大概率的token。

门控网络一般使用softmax或者sigmoid（选这个要做归一化），用于计算传入的token相对于每个expert的权重，门控函数满足两个目标：

**负载均衡：**直接根据softmax的概率分布选择最优秀的k个专家这种方法容易出现负载不均衡现象，即大多数令牌被分配到少部分专家，而其它专家都没有被分配过，即未训练到。
**规模效率：**在大规模数据（百万级输入）和专家数量（千级专家）下，通过高效的并行设计和资源利用，保持系统整体计算效率和资源利用率的能力。

门控网络中的设计：

1.专家容量：会限制专家处理的令牌数量低于某个阈值，N为训练批次中的总token数，E为专家数，而每个token可以发送给两个专家，则专家容量设置为O(2N/E),当有专家被选中的token数超出阈值时，token会被认为是溢出的(overflow)，此时g(S,E),即第E个专家对于第s个token的门控网络输出为零向量，也就是设置为未选中该专家，这些溢出的token会根据残差连接和MOE层的输出结合，输入到下一层。因此可以看出来，最终MOE输出的结果和每一层输入的数据Xs的size是保持一致的(在deepseek-v3开源出来的模型代码中，有用counts记录该批次中所有token分配给专家后，每个专家拥有几个token，但是未使用counts做这样约束)。如图所示，当token选择的expert，仅部分溢出，则只算另一部分未溢出的，而当token选择的expert全部溢出，则token将不做任何处理，直接按照残差链接的方式作为输出。

**2.本地组分发：**将训练批中的所有token均匀分配到G组中的本地组，每组包含S=N/G个token，并行处理，每组每个专家能分配的token数为2N/(G・E)，E为每组中的专家数，乘2是因为每个token能分发到两个专家。

**3.辅助损失：**l~~aux~~，被添加到模型的总损失函数中，，k为常数因子， $l_{nll}$ 为原损失， $l{aux}$ 为辅助损失，其中E为专家数， $c_e$ 表示某个专家分配到的token数(一般被token选定为first_expert，即最大概率专家的token的个数)，S是当前专家组包含的所有token， $\frac{c_e}{S}$ 理想状态下是 $\frac{1}{E}$ ，即完全的负载均衡，因此只要保证即可。而由于μ是一个常数，因此可以直接去掉，而因为 $c_e$ 是argmax操作，不可导，因此又引入me表示平均门限分数，即某个专家接收到的token的概率的平均值，这里的概率指当前token选择该专家的概率。

**4.随机路由选择：**MOE最终输出为选中专家（topk，deepseek-v3给的代码中是6)的加权平均数，在GSshard论文中说的是tok为2时，次优专家以其权重决定是否分配给第二个专家(比如权重比较小，可以选择不分配)，分配则该token分配了两个专家，否则只分配了一个专家。

这里Deepspeed做了不同的处理，首先1st expert是一定发出去的，而当选择2nd expert的时候，做了一些加噪的处理，即对输出的每个专家的logit，从某种分布中采样4个噪声，加上之后，mask掉第一个expert的logit，然后从剩下3个中找到最大的作为2nd Expert。

4.伪代码

"""
1. 通过gate，计算每个token去到每个expert的概率
【input】 :Attention输出的所有token，尺寸为(seq_len,batch_size,M)。其中M表示token_embedding
【reshaped_input】：主要是把token融合到一个维度，即变成(S,M)
【Wg】： 表示gate的权重，尺寸为(M,E),E表示专家的总数
【gates】：表示门控网络的输出，尺寸为【S，E】即每个token到不同expert的概率
""" 
M = input.shape[-1]
reshape_input = input.reshape(-1,M)
gates = softmax(einsum("SM,ME -> SE"),reshape_input,Wg)#可以看到门控网络计算后要做一个softmax把logit转化成概率

"""
2. 确定每个token最终要去的top2Expert，并返回对应的weight和mask
【combine_weights】：尺寸为(S,E,C),其中C表示专家可以接收的token的个数，这个矩阵表示每个token，对每个专家E的权重，而这个权重存放在buffer中的某个位置，如果不是目标位置就用0填充，比如对于图中的token0来说，它的combine_weights的子矩阵，即combine_weights[0,:,:]为：
	[	[p0,0,0,0],
		[p1,0,0,0],
		[0,0,0,0],
        [0,0,0,0],	]
 注意：combine_weights与gates算出来的权重不同，因为会对选中的top2个token再做一个归一化，并且可能是先random，选中的不一定是gates中次大的token。
        
【dispatch_mask】：尺寸为(S,E,C),它相当于把combine_weights有数值的位置改为True，而为0的位置则都为false，用来记录每个token在每个专家的每个buffer区域是否放置了这个token。
""" 
combine_weights,dispatch_mask = Tok2Gating(gates)

"""
3. 将token数据放置到对应的buffer区域
	【dispatched_expert_input】：尺寸为(E,C,M),我们在第二步拿到了dispatch_mask，dispatch_mask记录了每个token 应该放置在每个专家的buffer区的什么位置，因为放了就为1，没放就为0，因此我们根据dispatch_mask来放置reshaped_input中的每个token，就得到了expert的输入，即每个专家的每个缓冲区的token_embedding数据，如果此时缓冲区没有放满，就用zero向量填充。
""" 
dispatched_expert_input = einsum("SEC,SM->ECM",dispatch_mask,reshape_input)

"""
4. 进行expert计算
	expert也和FFN一样，由两个线性层，Wi和Wo组成
	【Wi】：尺寸为(E,M,H)
	【Wo】: 尺寸为(E,H,M)
	【expert_outputs】为expert的输出，大小为(ECM)，和输入的大小一样，即仅做线性变换
""" 
	h=einsum("ECM,EMH->ECH",dispatched_expert_input,Wi)
    h=relu(h)
    expert_outputs=einsum("ECH,EHM->ECM",h,Wo)
"""
5. MOE的输出：加权求和
	利用第二步得到的combine_weights，可以找到，每个token对于每个专家的概率，放置在每个buffer中。拿出这些概率和每个专家对应buffer上的token数据进行加权求和，得到最终结果。
""" 
	output=einsum("SEC,ECM->SM",combine_weights,expert_outputs)
    output_reshape=output.reshape(input.shape)

einsum在这里泛指我们自定义的某几种矩阵计算方式，它使得我们在计算矩阵计算的同时，能够维持token和expert的顺序

5.MOE混合并行训练

首先明确一点，在表示MOE的混合并行训练方式中，例如EP+DP，EP+TP+DP等等，都特质对MOE层的并行方式，而跟非MOE层没有任何关系，一般可能会采用MOE_GROUP来指定混合并行的方式。

TP2DP4+EP4(DP2)

DP2TP2+EP2(DP2).drawio (2)

如图为一个混合并行的示例，这里专门为了区分MOE层和非MOE层，使其使用不同的并行策略，非MOE层做TP2，DP4，而MOE层做EP4DP2，首先数据大小batch_size=8，被分成4份到4个TP组上，每个TP组再做2路tp，将非MOE层进行切分，而对于MOE层来说，做4路EP，即ep_group_size=4，将专家分到4组ep_dp_group上，ep_dp_group内部再做2路dp。

在一些框架中如(megatron)，为了复用已有的并行方式，少做修改，一般会强硬限制，若non-MOE做了tp切分，则MOE也必须做同样的tp切分，在此基础上再去安排MOE的ep等并行。

6.Deepspeed对ALL2ALL通信的改进

基本的ALL2ALL

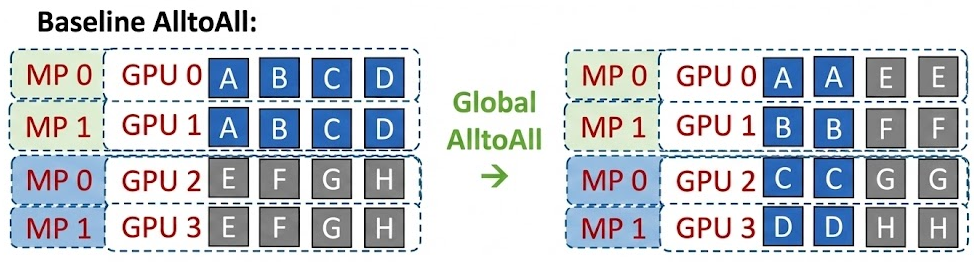
其中MP表示的就是TP，图中相关的分布式group为： TP_group[[0,1],[2,3]]

Ep_group[0,1,2,3]，即四张卡分别存不同的专家

这里描绘了ep_group首次做all2all的过程，将token发送到对应的expert上，看起来就像是做了一次矩阵转置操作，这里就体现了按照要去的专家位置排好顺序的意义，但是会发现同一个tp组因为做了allreduce，数据是一样的，那在all2all的过程中会被重复发送和计算，怎么减少重复呢？

理论的改进版All2all

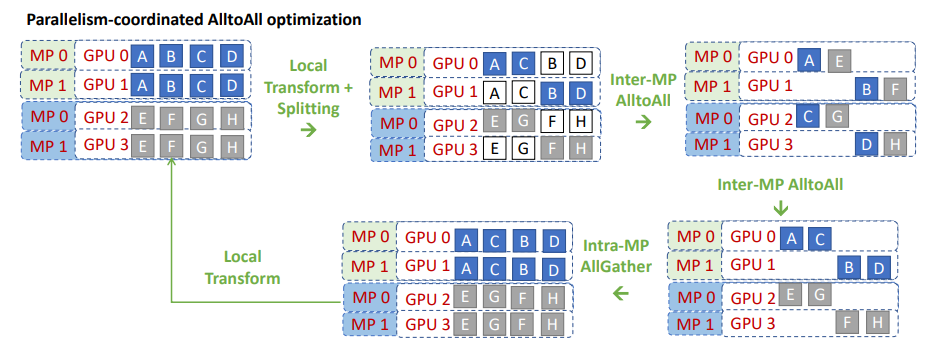
deepspeed改进版all2all的核心是：既然同一个tp组内的数据重复，那就在tp组内数据进行切分，每个tp组内的每块卡维护不同的数据，但是all2all group内一共有4张卡，如果要正常做all2all，卡上的数据和卡数应该相同。

因此更进一步的想法就是把all2all group也做切分，如图先做Local Transform之后，改变数据的排序，其实这里改变的是发送到专家的顺序，0卡只需要和2卡交换数据，1卡只需要和3卡交换数据，因此这里操作就是将每个tp组内，同一个rank号的tp构建为一组新的all_to_all通信组，这样就可以只用创建两个通信组，而同一tp组内的做数据的split，让每个tp上要发送和接收的数据都不一样，然后两两做all_to_all通信，经过MOE层处理后，再做一个all_to_all通信恢复，最后每个tp组内用一个allgather获得全量的数据。

deepspeed代码的实际操作All2All的方法

由于上述方法，将all2all的通信组直接改了，实际上适配会改动很多代码，因此实际操作时deepspeed并没有按上述方法做，而是用了一个叫**"drop_tokens"**的方法，因为每张卡的输出数据维度是(E,C,M),之前的切分之所以不行，其实是因为切分是在专家维度上切分，all2all通信也是专家维度，因此就导致要切all2all的groups，而可以发现，我们其实可以对每个tp组内，沿着C维度去切分数据，相当于一个tp组内，每个tp还是要处理发送和接收给所有专家token，但是每个tp只处理一部分的expert buffer中的要发送和接收的token，并且每个tp处理的数据都不一样。最后再通过一个all-gather操作，得到完整数据即可。

改进版的All2All（实际操作）注意事项

假设，MOE也做了tp的切分，这时候变成tp2ep2，即原来非MOE的tp组内加上了对epxert参数的切分，那么gpu0和gpu1此时分别包含epxert1的一半参数，这时候就不能用**"drop_tokens"**，因为虽然给到gpu0和gpu1的token是同一个，但是expert参数现在是partial状态，计算完后，要做allreduce才是最终的结果，所以此时gpu0和gpu1上的数据重复是有意义且必须的，因此就不能做drop_tokens了。

7.PR-MOE(Pyramid-Residual MoE DeepSpeed提出)

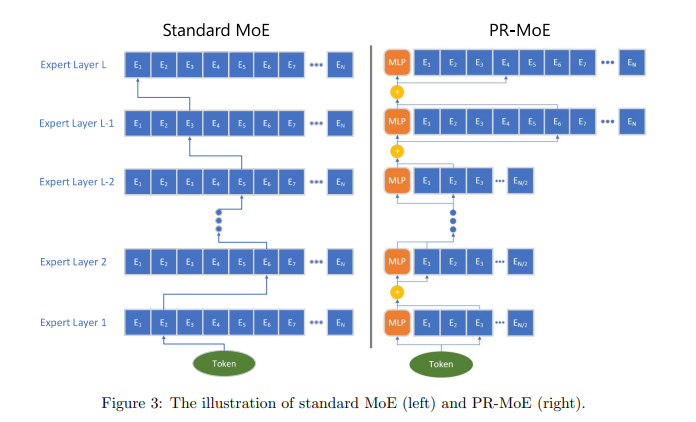
DeepSpeed还提出了一种自定义的PR-MOE，首先会让后面的层的专家数比前面的层的专家数多出一倍，所以看起来像是一个倒着的金字塔，也就是Pyramid，其次，DeepSpeed因为固定topKgate中的k为1或2，因此在PR-MoE中，当k为2时，top1的expert会被固定，即用一个固定的MLP代替可选的expert，仅仅对top2的expert进行选择，前者用来兜底，后者用来校准。相关代码如下：

output = self.deepspeed_moe(hidden_states, used_token)
if self.use_residual:
    # Residual MoE
    output_mlp = self.mlp(hidden_states)
    if type(output_mlp) is tuple:
        output_mlp = output_mlp[0]  # Ignore the bias term for now
    coef = self.coefficient(hidden_states)
    coef = torch.nn.functional.softmax(coef, dim=-1)
    output = output * coef[..., 0:1] + output_mlp * coef[..., 1:]
return output, self.deepspeed_moe.l_aux, self.deepspeed_moe.exp_counts

其中，coefficient是一个Linear层，输出大小为(hidden_size,2)，2即表示一份expert的权重，一份固定的mlp的权重。可能的一种训练后的理想效果是：当输入问题偏向专业领域，则给expert的权重更高一些；当输入问题偏向于通用领域时，则给固定的mlp的权重更高一些。

8.Megatron的SwitchMLP

与DeepSpeed不同的是，Megatron在做MOE时（默认使用TOP-1 expert），非MOE层和MOE层的TP_group是统一的，并且Megatron并不采用All-to-All进行通信，而是使用allgather+reducescatter，并且是drop_less的，也就是top-1 expert(这里只讨论默认情况)一定会发往它经过gate计算后概率最大的那个专家，所以它是如何保证通信的负载均衡的呢？

首先，在DeepSpeed中，会根据gate去计算每个token应该发往哪个设备上的expert，而由于可能存在，多个token都发往同一个expert，因此会早成all-to-all通信时的负载不均衡，因此，DeepSpeed中提出了一个capacity，用来限制expert可容纳的token容量，超出的就drop掉，没填满的就用zero padding填充。这样每个rank发送的通信量都限制在capacity，从而达到负载均衡。

而现在Megatron如果一定将token发往既定的expert，此时我们可能会想到出现复杂不均衡，然而，Megatron是用allgather，即每个ep_rank都直接拿到所有的数据（从这也可以看出通信量会增加），然后再去看哪些数据是属于当前rank上的expert需要处理的，把非当前rank上的expert需要处理的数据给mask掉（这里计算出来就是0），每个expert计算完成后，即使在TP下，也不做allreduce，而是用reducescatter，一方面把之前allgather过来的数据块，再按块返回给每个rank，另一方面将不同rank上的同一块数据做reduce，得到全局数据。

9.问题记录

1.输入到MOE-layer的输入，我们记输入数据的尺寸为(S,M),S是 $batch\_size*seq\_len$ ，为什么此时可以直接分裂一条语句的所有token，并且可以把多条语句的token融合计算？

因为对于FFN来说，在计算时，是不需要计算token之间的相对关系的，因此为了提升计算效率，通常都是将整个Batch里所有的句子的所有token混合在一起，并通过分布式处理来加速和降低显存。当经过FFN处理后，又会把所有token打包回来，恢复到之前的位置，即恢复成(batch_size,seq_len,hidden_dim)的形状，再输入给Multi-Attention层去处理。

2.Gshard中top2Expert如果选择的两个Expert都已经放满了，即溢流了，会怎么处理这些token？

**Drop tokens：**若单个token溢流，则只算另一个token，若两个都溢流，这个token直接通过残差连接的方式直接给到下一层，不做处理。会发现如果drop的token太多，会导致丢失太多信息，因为这些token都没有被expert处理，因此这也是后续优化的点。

3.Auxiliary Loss为什么引入me？

因为 $\frac{c_e}{S}$ 是不可导的， $c_e$ 的定义是某个专家buffer中已经存放下的token数（一般主要关注的是被token作为1st专家选中的那些token），而这个是一个argmax的操作，即调整某个Router对某个token的输出，即token发往各个专家的概率：

所以它无法正常做求导，但是如果引入 $m_e$ (该专家 buffer 中 token 的 avg(weight))，也就是所有token概率总和除以当前的token数，而这个值，会随着每个token选择该专家的概率值的改变而动态变化，并且变化是一个平滑连续的，此时 $c_e$ 相当于直接看成一个常数权重，如下：

从而让该Loss可导。

4.为什么每个expert的输入维度是(E,C,M)

首先为了保证每个expert都接收C大小的矩阵，如果有的expert buffer没有被填充满，则会用zero padding。

这里其实指的是单卡视角，因为每个专家能接受的token数量的能力是C，而每个token的隐藏状态的维度是M，又有一个专家，则如果在单卡上，可以直接把输入拼在一起，并且将专家参数拼起来，并且使用Batch Matrix Multiplication (BMM)计算，BMM计算的方式如下：

所以其实是利用GPU并行计算每个专家的输出。

如果是多卡分布式，那么每张卡只会计算(1,C,M)的数据。

5.Megatron和Deepspeed在做ep_group的通讯时的不同处理

deepspeed使用all2all通信，每个token是定向发送到它所对应的卡上，所以通信时会存在有的卡接收发送的token多，有的少。

megatron则使用的allgather通信，它不管token对应的expert是哪个，而是直接把数据全量发到每一个ep卡上，然后mask掉不是这张卡的expert维护的token，这样在通信时，ep_group时负载均衡的，缺点是发送大量的重复数据。

1.通信方式(NVIDIA NCCL标准)​

1.1 Broadcast​

1.2 AllGather​

1.3 ReduceScatter​

1.4 Reduce​

1.5 AllReduce​

1.6 All-To-All​

1.7 总结​

2. Paddle三类通信区分动手，动半，静态全自动​

3.分布式并行方式​

3.1 数据并行。​

补充说明：ZeRo(DeepSpeed,微软提出) 以及FSDP(Pytorch最新数据并行方案，ZeRo3和FSDP思想等价)​

Group Sharded：​

ZeRO-1(pytorch:OSS)：​

ZeRO-2(pytorch:SDP)：​

ZeRO-3(pytorch:FSDP)：​

FSDP(Fully Sharded Data Parallel)：​

3.2 张量并行(TP,MP)​

1 基础并行层​

1.1 ColumnParallelLayer与RowParallelLayer同时使用的关系​

1.2 ColumnParallelLayer与RowParallelLayer的w和bias的切分​

1.3 Vocab Parallel Embedding​

1.4 输出层的 Vocab Embedding​

2.TP的forward与backward过程​

3.Megatron中TP的使用​

3.3 流水并行(PP)​

FthenB​

1F1B编排​

激活重计算​

VPP​

Zero Bubble​

3.4 序列并行(SP)​

Megatron提出的序列并行​

通信与计算重叠(主要讨论Transfomer_Engine下的实现)​

allgather overlap(CommOverlapP2PBase::split_overlap_ag函数)​

reduce_scatter(CommOverlapP2PBase::split_overlap_rs函数)​

backward中的overlap(bulk overlap)​

3.5 上下文并行(CP)​

DeepSpeed的Ulysses​

Colossal-AI的Ring Attention​

Megatron的cp​

3.6 专家并行(EP)​

1.Gshard​

2.输入数据​

3.Gate(门控网络)​

4.伪代码​

5.MOE混合并行训练​

6.Deepspeed对ALL2ALL通信的改进​

7.PR-MOE(Pyramid-Residual MoE DeepSpeed提出)​

8.Megatron的SwitchMLP​

9.问题记录​

1.通信方式(NVIDIA NCCL标准)

1.1 Broadcast

1.2 AllGather

1.3 ReduceScatter

1.4 Reduce

1.5 AllReduce

1.6 All-To-All

1.7 总结

2. Paddle三类通信区分动手，动半，静态全自动

3.分布式并行方式

3.1 数据并行。

补充说明：ZeRo(DeepSpeed,微软提出) 以及FSDP(Pytorch最新数据并行方案，ZeRo3和FSDP思想等价)

Group Sharded：

ZeRO-1(pytorch:OSS)：

ZeRO-2(pytorch:SDP)：

ZeRO-3(pytorch:FSDP)：

FSDP(Fully Sharded Data Parallel)：

3.2 张量并行(TP,MP)

1 基础并行层

1.1 ColumnParallelLayer与RowParallelLayer同时使用的关系

1.2 ColumnParallelLayer与RowParallelLayer的w和bias的切分

1.3 Vocab Parallel Embedding

1.4 输出层的 Vocab Embedding

2.TP的forward与backward过程

3.Megatron中TP的使用

3.3 流水并行(PP)

FthenB

1F1B编排

激活重计算

VPP

Zero Bubble

3.4 序列并行(SP)

Megatron提出的序列并行

通信与计算重叠(主要讨论Transfomer_Engine下的实现)

allgather overlap(CommOverlapP2PBase::split_overlap_ag函数)

reduce_scatter(CommOverlapP2PBase::split_overlap_rs函数)

backward中的overlap(bulk overlap)

3.5 上下文并行(CP)

DeepSpeed的Ulysses

Colossal-AI的Ring Attention

Megatron的cp

3.6 专家并行(EP)

1.Gshard

2.输入数据

3.Gate(门控网络)

4.伪代码

5.MOE混合并行训练

6.Deepspeed对ALL2ALL通信的改进

7.PR-MOE(Pyramid-Residual MoE DeepSpeed提出)

8.Megatron的SwitchMLP

9.问题记录