Skip to main content

Flash_attention

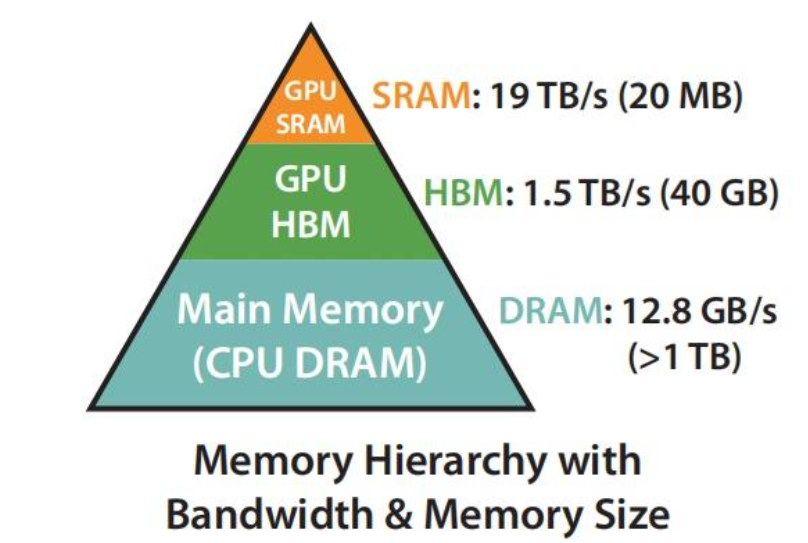
​ 首先明确一点，FlashAttention的提出，是为了解决在计算attention矩阵时，计算较慢的问题，因为一般会把整个大矩阵加载到HBM(High Bandwidth Memory)—高带宽内存；而现在希望将其加载到SRAM(Static Random-Access Memory)—静态随机访问存储器，如下图所示，展现了其计算速度。而由于SRAM存储容量较小，但计算Attention时的显存较高，一般需要的显存为O(N*N),Q,K,V∈R^N✖d^，因此，提出了FlashAttention，将Q,K,V矩阵分块，逐块加载到GPU的SRAM中计算，并且提出了在backward过程中，利用forward过程计算得到的softmax的归一化因子，在SRAM中快速重计算注意力矩阵，而不是一致保留forward过程的中间结果，而导致显存被持续较大占用，同时将注意力操作融合到一个GPU kernel中，避免从HBM多次读取和写入；最后进一步将其扩展为稀疏版，仅计算非零块的注意力矩阵，进一步降低内存访问次数和计算复杂度。

image-20250922173807694

1 safe_softmax​

​ attention的计算公式如下：

img

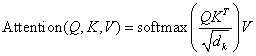
​ 首先这里需要明确，Q*K^^T^,是为了计算每个token和其它token的注意力（可以看作是token之间的相关性），并且S=Q*K^^T^/根号(d~k~)这里的softmax是针对S的每一行分别做softmax，即S经过softmax后的矩阵n*n的每一行的和为1。而这里除以根号(d~k~)是

​ Softmax 函数是机器学习和深度学习中广泛使用的归一化指数函数，主要用于将任意实数向量转换为概率分布，其计算公式如下：

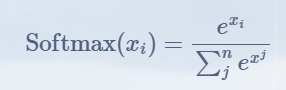
image-20250922175040657

​ 在计算 Softmax 时，即使数据类型为 FP32，当 时，分子 已经超过了 FP32 的范围。Safe Softmax 通过减去中的最大值，来避免数据溢出，其公式如下： $$ \text{Safe-Softmax}(x_i)=\frac{e^{x_i-m}}{\sum_j^ne^{x_j-m}},m=\max(x_1,x_2,\ldots,x_n) $$ ​ 因为 ，x~i~-m<0所以避免了分子数据溢出。

2 online_softmax​

​ onlinesoftmax的提出，主要用于服务flash_attention，因为flash_attention将WQ,WK,WV,WO进行了分块，而在计算softmax的时候，是整个self_attention矩阵的每一行，计算一个softmax，所以一般来说需要获得这一行全部的数据，才能计算出，这一行每一个token的softmax，因此在计算时，需要流式计算。同时从本质上来说，计算safe softmax的时候，要首先遍历一遍，得到最大值m，再遍历一遍得到分母，即所有x~j~-m的总和，最后遍历一遍，计算每个softmax(xi)；而使用online_softmax，计算如下： $$ m_i=\max(m{i-1},x_i) $$

$$ d{i-1}=e^{x{1}-m{i-1}}+...+e^{x{i-2}-m{i-1}}+e^{x{i-1}-m_{i-1}} $$

$$ di=d{i-1}\cdot e^{m_{i-1}-m_i}+e^{x_i-m_i} $$

​ 每次输入进来新的xi时，此时新的mi，即为之前的最大值mi-1和当前的xi中的最大值。

​ 而di则等于，把所有的求和项的，m~i-1~换成m~i~，并且加上最新的第i项，即如上式所推导。

3 FlashAttention​

​ 沿着序列维度，即seq_lenth进行切块

​ 主要在训练时，可以并行计算token的attetion时使用

​ 算法流程图如下：

image-20251024134404074

​ 算法公式解读：

​ Step 1.首先Q,K,V∈R^N×D^保存在HBM上。

​ 设置 $$ B~c~ = \lceil \frac{M}{4d} \rceil $$，这里B~c~是K,V分块的大小，按行切分，M是SRAM的大小，除以4d是因为要同时存放Q,K,V,O四个矩阵的数据。

​ 设置$$ B~r~ = min(\lceil \frac{M}{4d} \rceil,d) $$，B~r~是Q分块大小，按行切分。注意M被分成了Bc*4d，即假设Q,K,V,O都是Bc*d的大小，但是注意我们还要保存中间计算变量，而中间计算变量最大的就是S∈R^Br×Bc^，假设Bc大于d，则取d，目的是让S的大小不超过Bc*d，从而可以用Q∈R^Br×d^则能放下S，否则Br*Bc>Br*d，Q就放不下这临时变量了，用Q放是因为，内循环是Q块，Q此次计算后，在内循环就用不上了。

​ Step 2.预留结果暂存空间Q,K,V∈R^N×D^保存在HBM上。

​ O是最后的输出，l是最终对于N行，每轮计算后，每一行的sum(P~ij~)，m是N行每轮计算后，每一行的最大值S~ij~。P~ij~即e^S~ij~-m~ij~^。所以l其实就是softmax的分母，只不过因为分块原因，这个分母总是一个临时的，直到最后一次计算。

​ Step3.将矩阵分块

​ T~r~是Q的分块数，T~C~即K,V的分块数。

​ Step4.双重循环逐步计算O~i~*（过程中更新softmax）

​ 外循环为K,V，Load一个K,V块从HBM到SRAM，循环Load每一个Q~i~，O~i~，l~i~，m~i~，每次计算出一个S~ij~，注意因为Q~i~是按行分块，所以每一次内循环，其实是为每一行算出一个S注意力矩阵，这个S在这一次内循环中是相互不影响，且不会存在m~ij~，l~ij~的多次更新的，而是每一轮新的K~j~，V~j~和Q~i~计算时，要对前一次的m~ij~，l~ij~进行更新，同时新的m~i~很好理解，就是取第i行，当前块$$ \hat{m}_{ij} $$和前面块m~i~的最大值，而l^new^~i~的计算，之所以是这样的，前半部分其实是更新原来的l~i~中减去的最大值m~i~，而后面部分其实是因为，前面已经把当前第i行的l~ij~算出来，所以，这里再把对应的m~i~也更新一下即可。两个加起来就是最新的l~i~。因为l~i~和m~i~更新了，因此这里还要更新之前计算的O~i~，并计算此时的O~i~，然后二者是累加的关系，从而得到最新的O~i~。

​ 手推li和Oi更新的公式如下：

image-20251024163242522

image-20251024163347228

​ 这里最重要的一点是，在此处更新O~i~的时候需要构造对角矩阵（这里也暗示了flashattention的一个缺点，由于对角矩阵的存在引入了额外的计算开销）。

​ 为什么构建对角矩阵，上面的手推公式已经证明，上面公式有个错误应该是e^mi-mi_new^也需要构建对角矩阵，否则维度不匹配。

​ 如下是整个flash_attention的计算过程的图形示意：

普通attention计算（为了和FlashAttention对齐，做了矩阵拆分，实际运算时，整张矩阵做运算）：

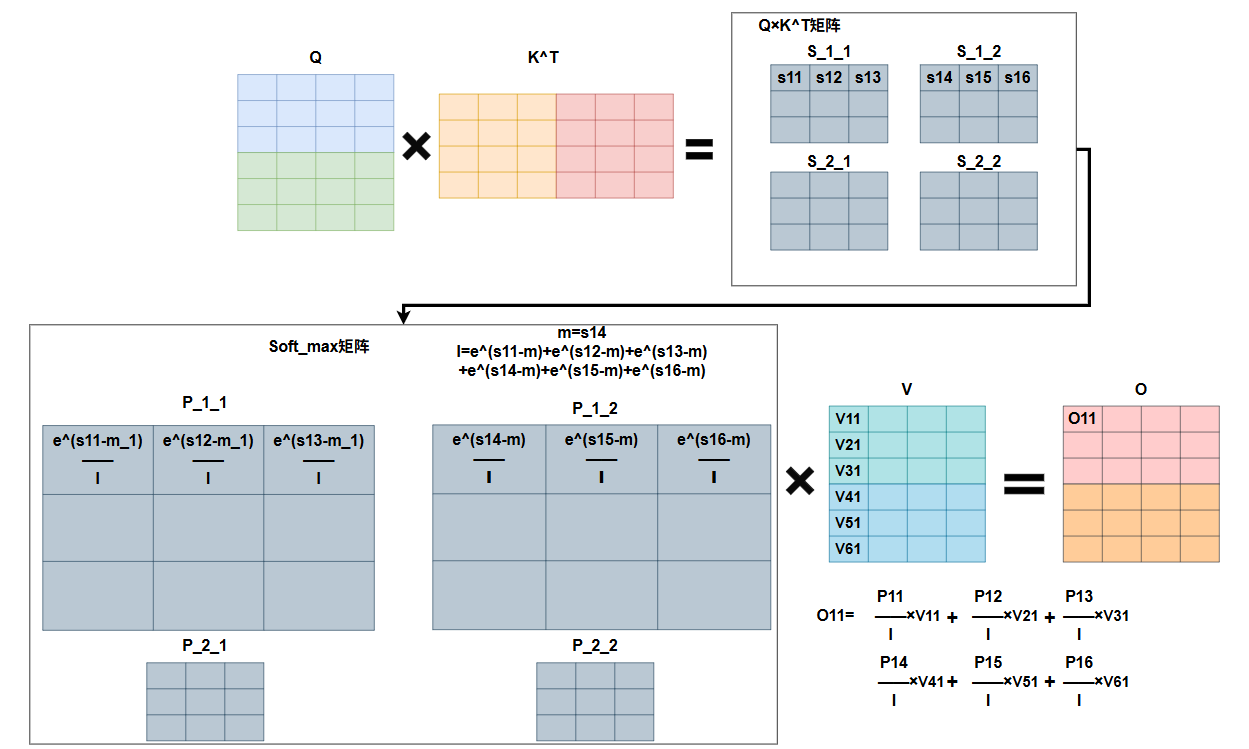
image-20251024211407104

Flashattention计算：

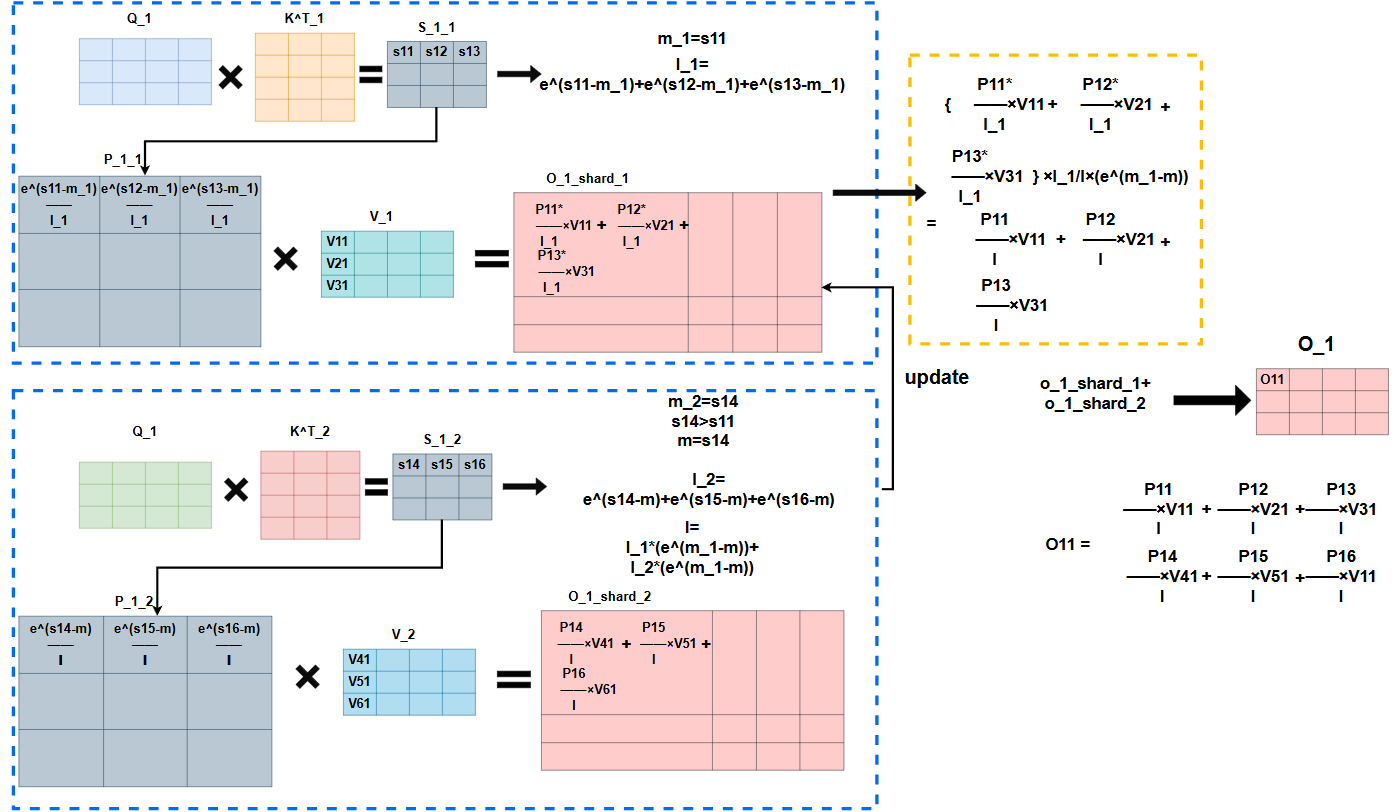
image-20251024211504084

​ 可以看到采用ring_attention的思想，Q_1会在两次外循环后，分别和全部的K矩阵相乘，而最后一次计算完成后，才能完全确认第i行最大的m，从而确认l。算法当中每次是先用当前第i行的最大值作为mi，去计算li，但其实可以直接将当前这一行的最大值和m_max_old作比较，得到截止到目前这个块，第i行的最大值，从而确认l，否则还会重复计算，因此这里我认为可以优化一下。

​ 而由于Q_1经过第一次外循环计算出来的O_1均是基于m_1与l_1的，而softmax是需要用全局的m与l的，因此这时候要重新计算O_1，即*l_1/l，这一步是将分母替换成l，而分子中的Pij中的每一项，同样是用的Sij-m_1，要替换成-m，因此*e\^（m_1-m）做替换。又由于，对于整个O_i来说，这里替换的其实是li和mi，都是∈R^Br^，即一维向量，而对于O_i的每一行，都要乘以li向量对应的每一个值，所以将li转换为对角矩阵，即用li向量的每个值构建对角线，其它均为0，即可实现，这里我认为e^mi-mi_new^也需要构建对角矩阵，公式中应该是笔误，否则维度不匹配。

3.1 FlashAttention存在的一些问题​

​ 1.FlashAttention在反向时会重计算，用时间换空间

​ 2.由于对角矩阵的存在，会引入额外的计算开销，造成资源浪费

3.2 FlashAttention正向代码手撕​

import torch
import math 
# 论文中 QKV 的形状为(N,d)，对应到这里为(seq_len,head_dim)，假设Q的形状为(batch_size,seq_len,head_dim)
def falsh_attention(query,key,value,mask=None)
    #负无穷大
    neg_inf = float('-inf')
    # epsilon 防止除0
    epsilon = 1e-6
    #N,d
    seq_len = query.size(-2)
    head_dim = query.size(-1)
    # 预留 output
    output = torch.zeros.like(query,device=query.device,dtype=torch.float16)
    # 记录分块 softmax 中的最大值 ,去掉query的最后一个维度，则m的大小为[batch_size,seq_len)，再增加一个大小为1的维度，因为m是取head_dim维度里面的最大值，所以用unsqueeze，最后乘以neg_inf，初始化，最大值都是负无穷大
    m = torch.ones(query.shape[:-1],device=query.device,dtype=torch.float16).unsqueeze(-1)*neg_inf
    # 记录分块 softmax 的和
    l = torch.zeros(query.shape[:-1],device=query.device,dtype=torch.float16).unsqueeze(-1)
    
    # KV 的行分块大小，由M决定，M为SRAM的大小，向上取整，分更多的块
    B_c=math.ceil(M/4*head_dim)
    
    # Q的行分块
    B_r=min(B_c,head_dim)
    # KV的分块数
    T_c = math.ceil(seq_len/B_c)
    T_r = math.ceil(seq_len/B_r)
    #Q,K,V分块
    query_blocks = torch.split(query,B_r,dim=-2)
    key_blocks = torch.split(key,B_c,dim=-2)
    value_blocks = torch.split(value,B_c,dim=-2)
    #Mask分块,mask/mask_block维度为N*N/Br*Bc,与S维度相同，沿着最后一个维度切，即列切，所以是B_c，即沿着head_dim,因为每次算出来Si都是第i行的部分列的数据。
    mask_block = torch.split(mask,B_c,dim=-1)
    # output、m、l分块;元组不支持按索引修改，而列表支持,后续要更新output、m、l
    output=list(torch.split(output,B_r,dim=-2))
    m_block=list(torch.split(m,B_r,dim=-2))
    l_block=list(torch.split(l,B_r,dim=-2))
    
    #分块计算注意力
    for j in range(T_c):
        key_j=key_blocks[j]
        value_j=key_blocks[j]
        mask_j=mask_block[j]
        for i in range(T_r):
            query_i=query_blocks[i]
            output_i=output[i]
            m_i=m[i]
            l_i=l[i]
            #计算S
            S_ij=torch.matmul(query_i,key_j.transpose(-2,-1))/(head_dim**0.5)
            #mask
            if mask_j is not None:
                S_ij=S_ij.masked_fill(mask_j.unsqueeze(1)==0,float('-inf'))#应该是扩展成（batch_size,head_num,seq_len,head_dim），若某个维度不匹配，则广播数据，即复制此维度的子维度,这里设置负无穷是因为经过soft_max后会趋近于0
            m_ij=torch.max(S_ij,dim=-1,keepdim=True)
            #这里先用局部最大值算，而不是全局最大值，主要是较小的m可以保证数值较为稳定，同时使得Pij计算出来的数值精度较高，而保证lij计算出来的数值精度较高
            P_ij=torch.exp(S_ij-m_ij)
            l_ij=torch.sum(P_ij,dim=-1,keepdim=True)+epsilon
            m_i_new=torch.max(m_ij,m_i)
            #逐元素相乘，因此用*，都是[Br,1]的形状
            l_i_new=torch.exp(m_i-m_i_new)*l_i+torch.exp(m_ij-m_i_new)*l_ij
            
            #计算并更新output,l_i和torch.exp(m_i-m_i_new)都是Br*1，在与output_i做乘法时会进行广播，从而扩展到Br*d,再逐元素相乘
            output[i]=(l_i*torch.exp(m_i-m_i_new)*output_i+torch.exp(m_ij-m_i_new)*torch.matmul(P_ij,value_j))/l_i_new
            m[i]=m_i_new
            l[i]=l_i_new
    #拼接结果
    output=torch.cat(output,dim=-2)
    return output