DualPipe学习记录
Deepseek V3选择仍使用ZeRO-1
采用了16路流水并行和64路专家并行
1.Zero Bubble Pipeline Parallelism
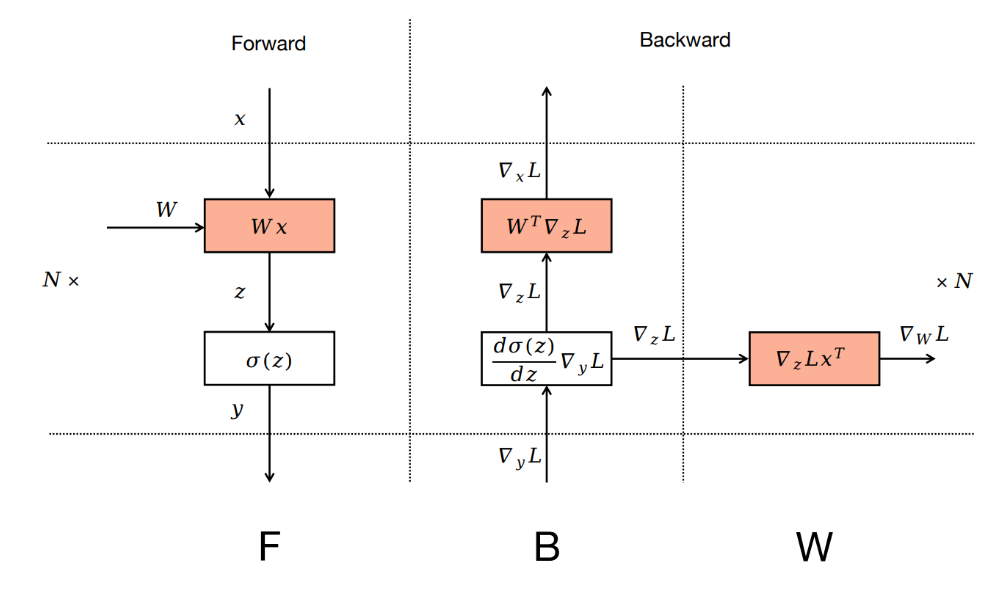
这里B是做梯度计算,W是做梯度更新,往常来说,是所有backward做完,才一次性做所有的参数更新,分开后,即一个b一个w
B对应输入的activation x求导(在模型中可以看做隐藏层结果计算这一步,对隐藏层yi求导),W即对权重w求导,backward过程中,第i-1层的梯度计算,只需要得到第i层输入xi(等价第i-1层输出,yi-1)的梯度,因此第i-1层的B阶段依赖于第i层的B阶段,而只依赖于,在计算完成后即可。
ZeRO-1即使用的zero_bubble策略
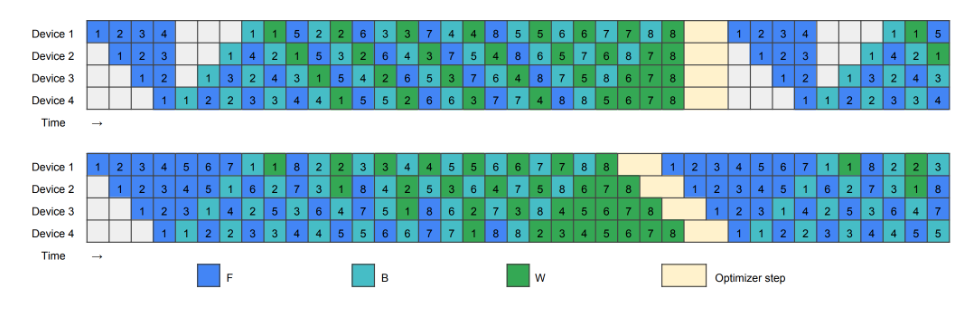
ZB1(上图)即峰值显存约为4个micro_batch,ZB2(下图)即峰值显存增加为8个micro_batch
2.专家并行
读Gshard理解专家并行:GShard: Scaling Giant Models with Conditional Computation and Automatic Sharding:链接:[2006.16668] GShard: Scaling Giant Models with Conditional Computation and Automatic Sharding
在MoE(mixture of expert)网络中,包含expert部分,门控网络,以及all to all操作, FFN的输入为attention层的输出归一化后的结果。
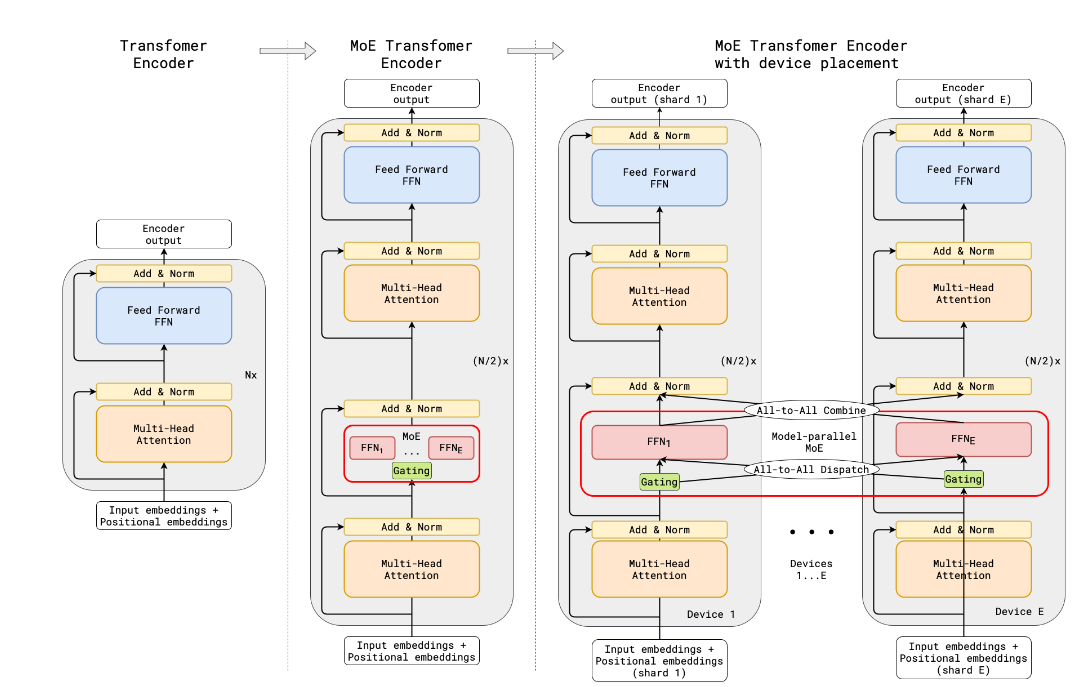
2.1 forward阶段
forward过程中,包括了四个主要的步骤:
- multi-head Latent attention层的计算;
- all-to-all dispatch,信息分发到各个node;为的是计算moe做准备(总是需要把token分发到M个机器上)
- model parallel MOE,模型并行MOE,也就是deepseekMOE;各专家独立执行FFN,即多个Experts,(仅仅前n_dense_layers个为MLP层,其它都为MOE层,一般n_dense_layers=1,在671B模型中,n_dense_layers=3);
- all-to-all combine,M个机器的MOE计算完成之后,将各专家的输出加权求和,返回最终结果。
即 ATTN(F)->DISPATCH(F)->MLP(F)->COMBINE(F)
forward具体数据流:
前向过程的整体流程是输入一个batch的数据,紧接着对每个token进行embedding,采用RMSNorm做归一化,接着输入到MLA层进行注意力的计算,紧接着将attention的输出结果和embedding后的输入进行相加,并经过RMSNorm归一化,得到MLP层的输入,输入后会通过门控网络选择相关的专家,紧接着使用 all to all dispatch将结果发送到选出的专家,每个设备上用当前同一批专家做计算,在经过all to all combine 将结果聚合,得到当前block的输出。
2.2 backward阶段
与前向过程反过来求梯度
COMBINE(B)->MLP(B)->DISPATCH(B)->ATTN(B)

而deepseek_V3又将其backward阶段分为了B和W,即B对应输入的activation x求导(在模型中可以看做隐藏层结果计算这一步,对隐藏层yi求导),W即对权重w求导,backward过程中,第i-1层的梯度计算,只需要得到第i层输入xi(等价第i-1层输出,yi-1)的梯度,因此第i-1层的B阶段依赖于第i层的B阶段,而只依赖于,在计算完成后即可。
backward具体数据流:
在进行backward时首先计算损失函数梯度,即对模型输出y的梯度,紧接着采用all to all
2.3 门控网络
使用softmax或者sigmoid(选这个要做归一化),用于计算传入的token相对于每个expert的权重,门控函数满足两个目标:
- 负载均衡:直接根据softmax的概率分布选择最优秀的k个专�家这种方法容易出现负载不均衡现象,即大多数令牌被分配到少部分专家,而其它专家都没有被分配过,即未训练到。
- 规模效率:在大规模数据(百万级输入)和专家数量(千级专家)下,通过高效的并行设计和资源利用,保持系统整体计算效率和资源利用率的能力。
门控网络中的设计:
-
专家容量:会限制专家处理的令牌数量低于某个阈值,N为训练批次中的总token数,E为专家数,则专家容量设置为O(N/E),当有专家被选中的token数超出阈值时,token会被认为是溢出的,此时g(s,E),即第E个专家对于第s个token的门控网络输出为零向量,也就是设置为未选中该专家,这些溢出的token会根据残差连接和MOE层的输出结合,输入到下一层。因此可以看出来,最终MOE输出的结果和每一层输入的数据的size是保持一致的(在deepseek-v3开源出来的模型代码中,有用counts记录该批次中所有token分配给专家后,每个专家拥有几个token,但是未使用counts做这样约束)
-
本地组分发:将训练批中的所有token均匀分配到G组中的本地组,每组包含S=N/G个令牌,并行处理,每组每个专家能分配的token数为2N/(G・E),E为每组中的专家数。
-
辅助损失:,被添加到模型的总损失函数中,
,k为常数因子,为原损失,中E为专家数,Ce/S 表示输入路由到每个专家上的分数,me表示平均门限分数。
-
随机路由选择:MOE最终输出为选中专家(topk,deepseek-v3给的代码中是6)的加权平均数,在GSshard论文中说的是tok为2时,次优专家以其权重成比例的概率决定是否分配给第二个专家,分配则该token分配了两个专家,否则只分配了一个专家。
2.4 Expert网络
输入为 attention经过标准化后的输出,一般为全连接层,被选中的expert将进行计算,在经过all to all通信,将每个专家网络的输出发回给原来的请求设备,进行加权求和,得到当前block的输出。
2.3 Attention层
一般就是transformer的attention层
3.Deepseek-v3中的模型层
3.1 基础模型结构
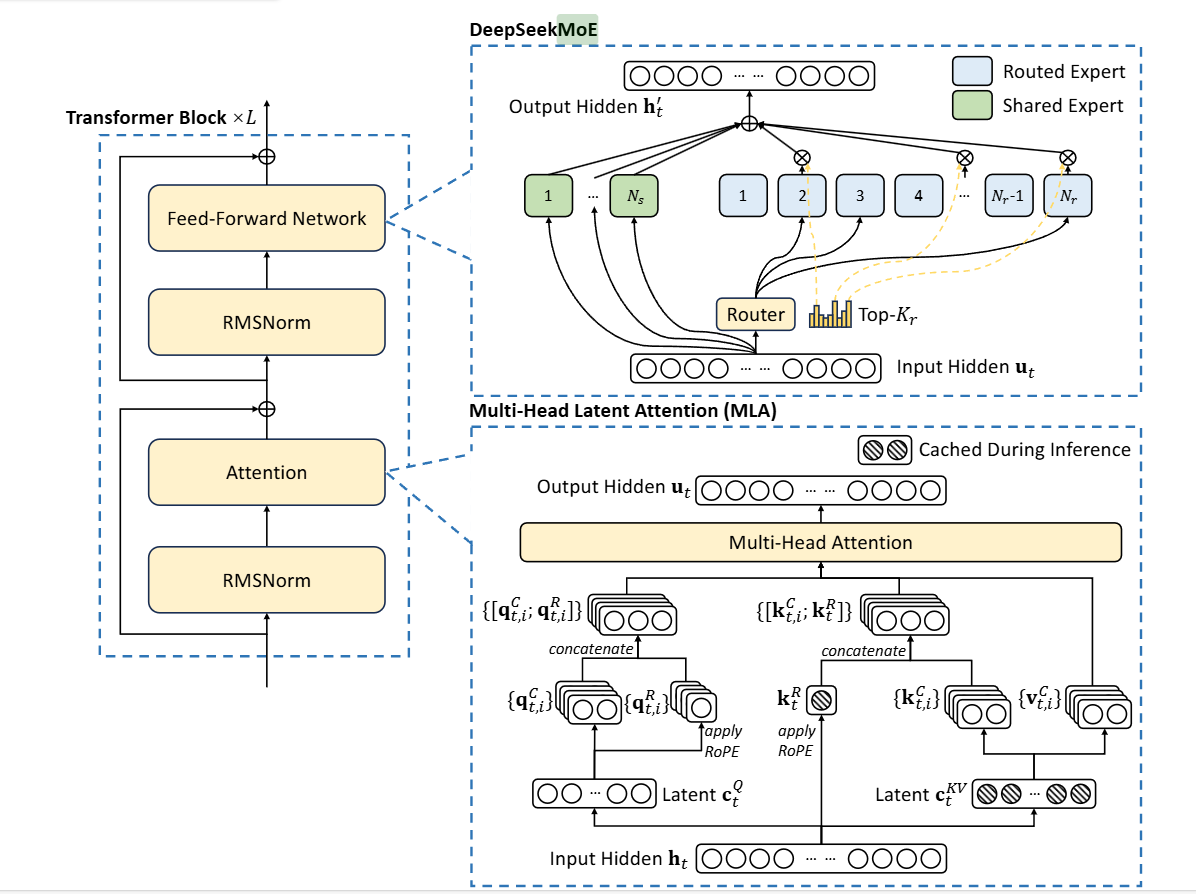
RMSNorm为均方根标准化,公式如3.1所示,其中RMS(x)如公式3.2所示,γ为可学习参数。FFN即为DeepSeekMoE,Attention部分,即为MLA。
公式3.1
公式3.2

3.2 DeepSeekMoE
其中,shared Expert为Worker之间共享的,参数也会同步共享,而Routed Expert则是路由专家,每个Worker独有的,在门控网络部分,即如图的Router部分,Deepseek-V3中引入了无辅助损耗负载均衡,同时使用sigmoid函数作为亲和力得分的计算。具体公式如下:
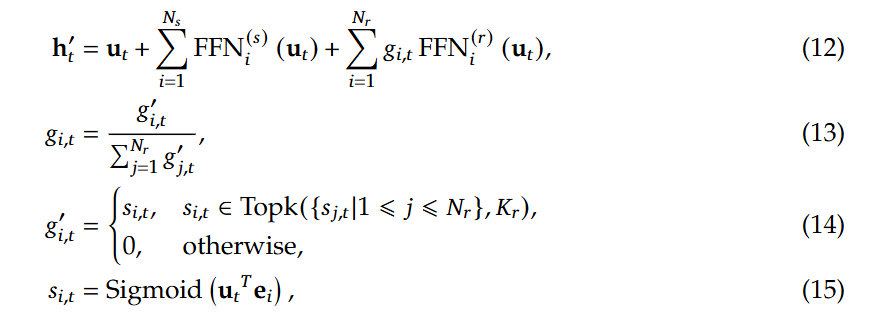
这里的 的每一项分别为 input hidden 、共享专家输出之和,以及路由专家的加权求和,这里的权重是通过对每个归一化得到的,除了tok个最大的亲和力得分的为,其它均为0,这里的即门�限值,即与FFN输出相乘的权重。是第i个专家的质心向量:在特征空间中,一个类别或簇的所有样本的特征向量的平均值,代表该类别/簇的中心位置。
而无辅助损耗负载均衡(Auxiliary-Loss-Free Load Balancing),对应公式如下,在训练步骤的每个批次,会对专家负荷进行监控,每一步结束时,对应的专家超载,则将偏差项减小γ,若负载不足,则增大,其中 γ 是一个称为偏差更新速度的超参数,偏置b只用于负载均衡。
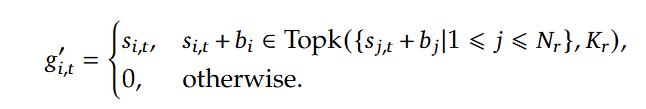
为了防止任何单个序列内的极端不平衡,还采用了一种互补的顺序平衡损耗,
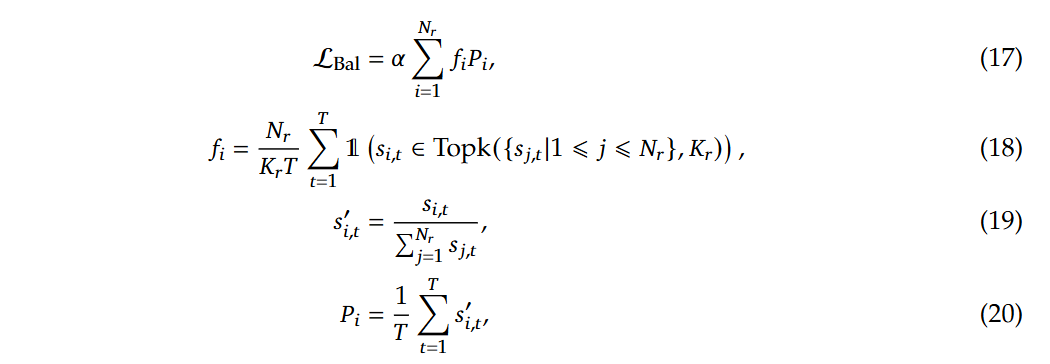
如公式(19)所示,为第i个专家对于第t个token的亲和力得分在所有专家对于该token的亲和力得分下的标准化,而公式(20)得到的即为第i个专家对于所有的token的亲和力得分标准化后的均值,对于,T表示序列中标记的数量,因此该公式表示(整个序列的所有token对于第i个专家的平均最大亲和力得分,以top_k和T值做平均)*,即路由专家的个数。α是一个超参数,会设置为一个很小的值。
3.3 MTP Modules
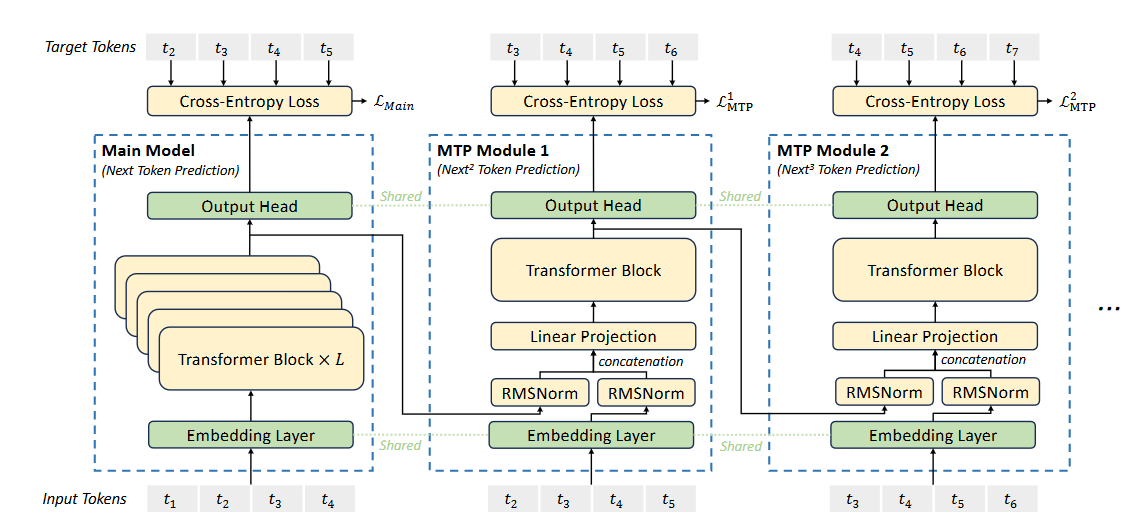
4. DualPipe的实现逻辑
4.1 一些注意事项:
1. 路由专家必须能均分到各个设备上
- 文章提到每个token最多分配到4个node上(大概是最多分配给四个机器上)为了有效地利用 IB 和 NVLink 的不同带宽,这样,通过 IB 和 NVLink 的通信完全重叠,每个令牌可以有效地选择平均每个节点 3.2 个专家。
- 从model.py代码中看出,一个transformer网络由多个block组成,每个block都含有一个MOE网络,而在每个MOE网络中,都会初始化专家网络,因此每一个block的专家是独立的:
self.experts = nn.ModuleList([Expert(args.dim, args.moe_inter_dim) if self.experts_start_idx <= i < self.experts_end_idx else None for i in range(self.n_routed_experts)])
- 同时通过rank来控制每个设备上的专家分配是均匀的:
self.n_local_experts = args.n_routed_experts // world_size
self.n_activated_experts = args.n_activated_experts
self.experts_start_idx = rank * self.n_local_experts
self.experts_end_idx = self.experts_start_idx + self.n_local_experts
- 通信细节:
- 使用 Warp Specialization 技术,将通信任务划分为 IB 发送、NVLink 转发、接收三个阶段,动态分配 GPU 线程。
- 利用 PTX 指令 优化通信块的 L2 缓存访问,减少对计算核心(SM)的占用。
4.2 核心编排部分(通信与计算重叠)
4.2.1 核心编排解读

相比于ZB-PP,除了F,B,W的拆分外,DualPipe还在通信/计算的维度上拆分任务,将F和B过程进一步拆分为:
- 计算:MLP(F),MLP(B),ATTN(F),ATTN(B)
- 通信:DISPATCH(F)DISPATCH(B),COMBINE(F),COMBINE(B)
通过调节GPU的流处理器的分配比例,可以保证通信部分的时间和计算的时间匹配上(即途中的上下两行对齐的效果),从而省去因通信而产生的GPU计算空闲。
在模型层分配的设计上,DualPipe中采用了如下的设计:
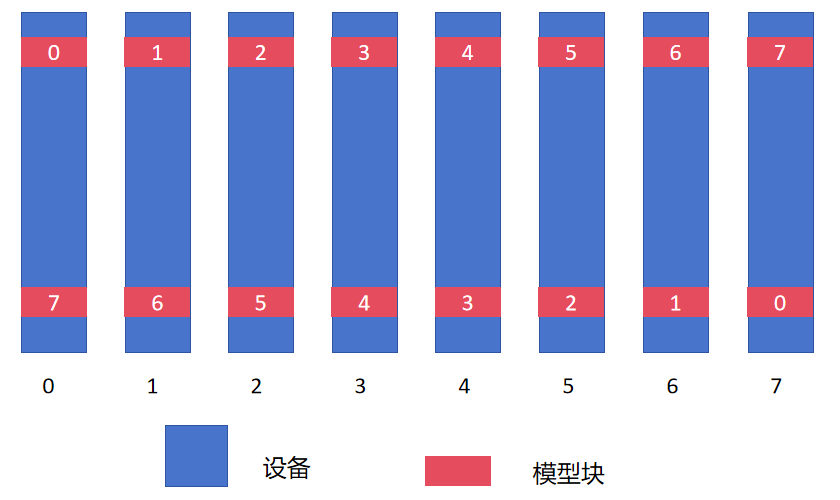
这样的设计使得在前向和后向计算时卡间的顺序都可以保持一致,不同卡上的同一组参数其更新时间也可以保持一致(由图中的上下对称性可知)。同时从两端输入批次进行训练。
以下是dualpipe的编排情况,如下图所示:

其中:
对应

这样做可以在执行过程中,完全隐藏: all to all和 PP 通信
选用all to all 的原因
- 动态路由的不可预测性,无法提前确定通信目标。
- 批次内专家覆盖的全局性,导致设备间需交换全量数据。
- 硬件优化的集体通信效率,远高于动态点对点通信。
- 反向传播的对称性需求,确保梯度正确传递。
通信与计算overlap部分的分析:

红色箭头和蓝色箭头分别代表一个micro_batch,因为每个设备上保留了两个模型块,所以分别是从设备0 和设备 7 对称开始,在某个阶段,在同一个设备上,出现一个模型块做forward,另一个模型块做backward,并且编排后可重叠计算与通信。
此时需要注意的一个点,从Time的指向来看,先进行了dispatch(F),然后是MLP(F),但是通过模型层我们可以发现,正常来说应该是先进行attn(F),再把attn(F)的结果dispatch出去,因此笔者认为,此时的dispatch(F),MLP(F),COMBINE(F)均为上一个block的forward,而attn(F)为下一个block的forward部分,一个block代表一个隐藏层,每个设备上有多个block
猜测:图中紫色的PP部分是在backward之后进行权重梯度同步
4.2.2 attention后的dispatch在代码中的具体体现
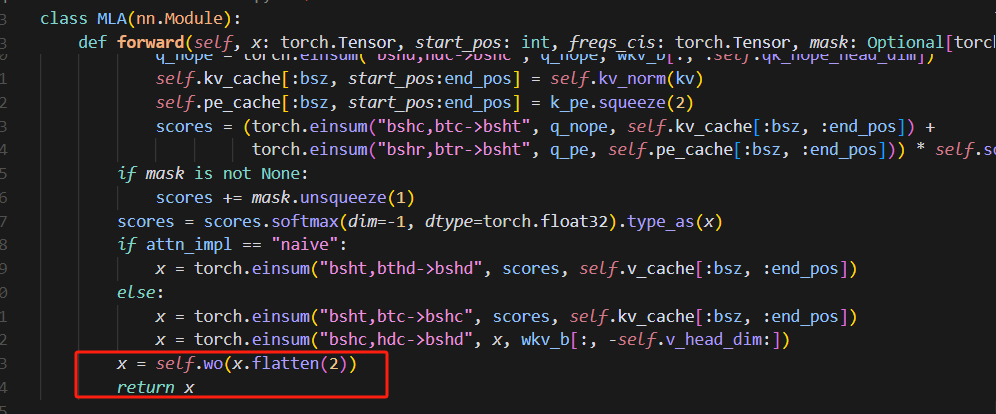
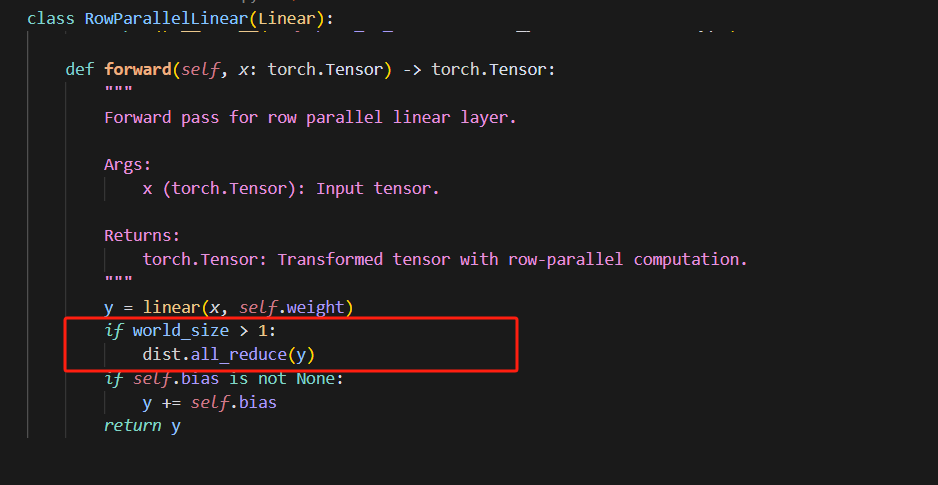
在attention阶段,是多个设备并行计算,再使用all_reduce,最终每个设备上都有了attention后的结果,在MOE阶段,其它设备的专家就可以并行处理这个值。
4.2.3 MOE后的combine在代码中的具体体现
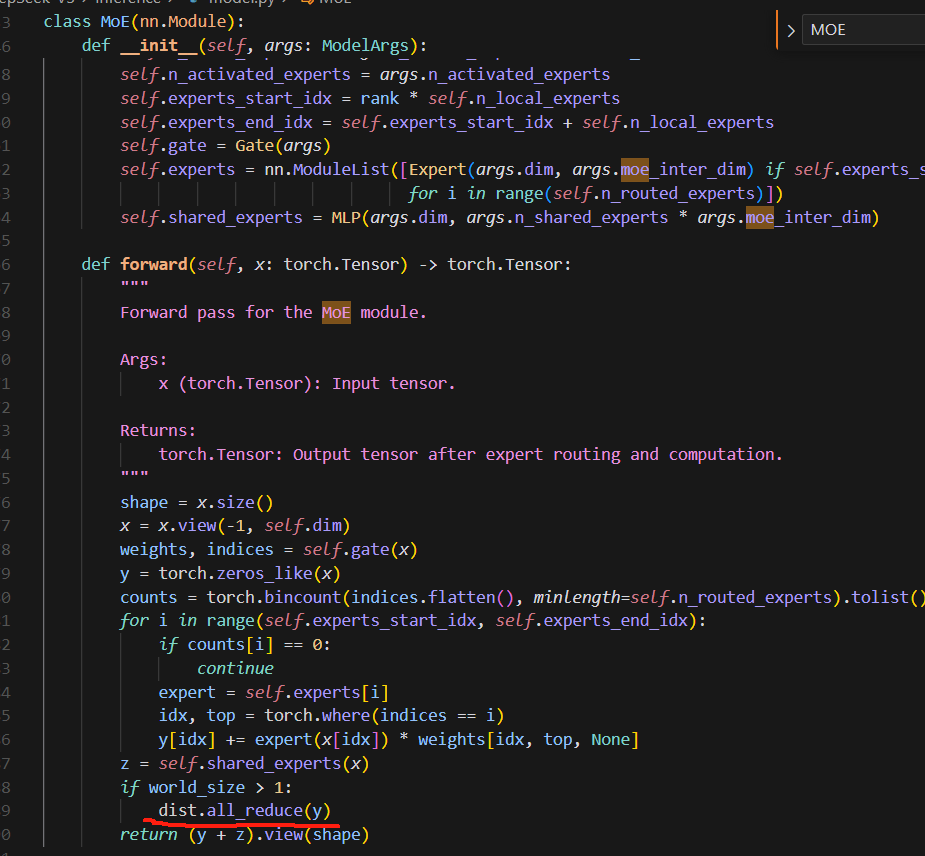
多个专家处理完y以后,将其累加,得到MOE的输出结果,即combine
4.3 对应bubble与峰值显存值分析:

bubule分为四个阶段计算:=B-W(表示对输入求梯度)
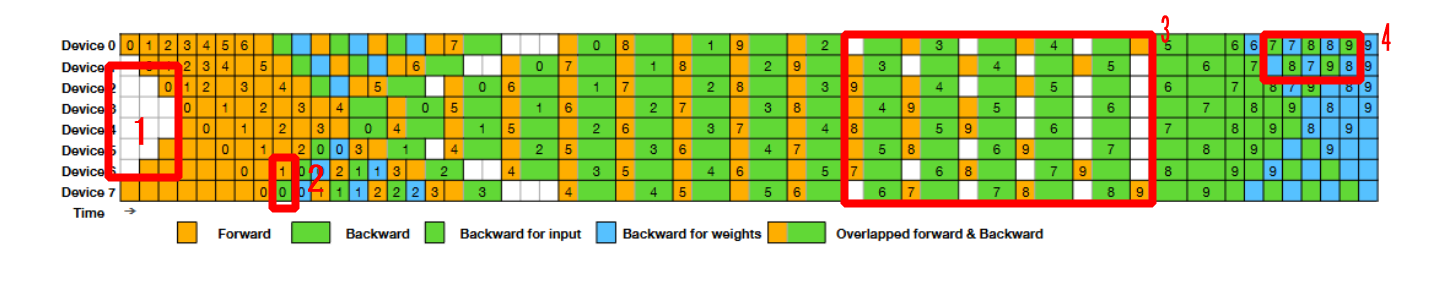
(1) 在forward过程中机器等待造成的buble,这里之所以是pp/2,是因为整个流水并行是相对中间对称的,因此经过最中间的设备后,无需再等待。
(2) 与F的时间差
(3) F&B与一个backward的时间差
(4) 与W的时间差
4.4 编排分析

原论文未给出编排逻辑,因此在此做了自行总结
首先可以发现的是,整个规律分为
- warm_up部分,先做一些forward,然后做1F1B+最后一个F
- steady部分,做F&B,可能包含F不够了,只做backward的部分。
- cool_down部分,对剩余的backward进行排列
- acc_step>=pp_degree
4.4.1 pp_degree=4,acc_step=4

规律:
- GPU1 和 GPU 4 有 实际的3 个 F & B,GPU 2 和 GPU 3 有 4 个 F & B
- GPU1经过一个 模型块2的1F1B(即F做完,立刻�做B)后,再经过一个模型块2的1F,开始做(3+2) 个F&B,并且是两个模型块交替进行,若此时模型块1的forward部分的micro_batch不够了,则只添加模型块2的backward;GPU4与之刚好相反排列。
- GPU2编排两组两个模型块交替的forward后,开始做(4+2) 个F&B,并且是两个模型块交替进行,若此时模型块1的forward部分的micro_batch不够了,则只添加模型块2的backward,GPU3与之刚好相反排列。
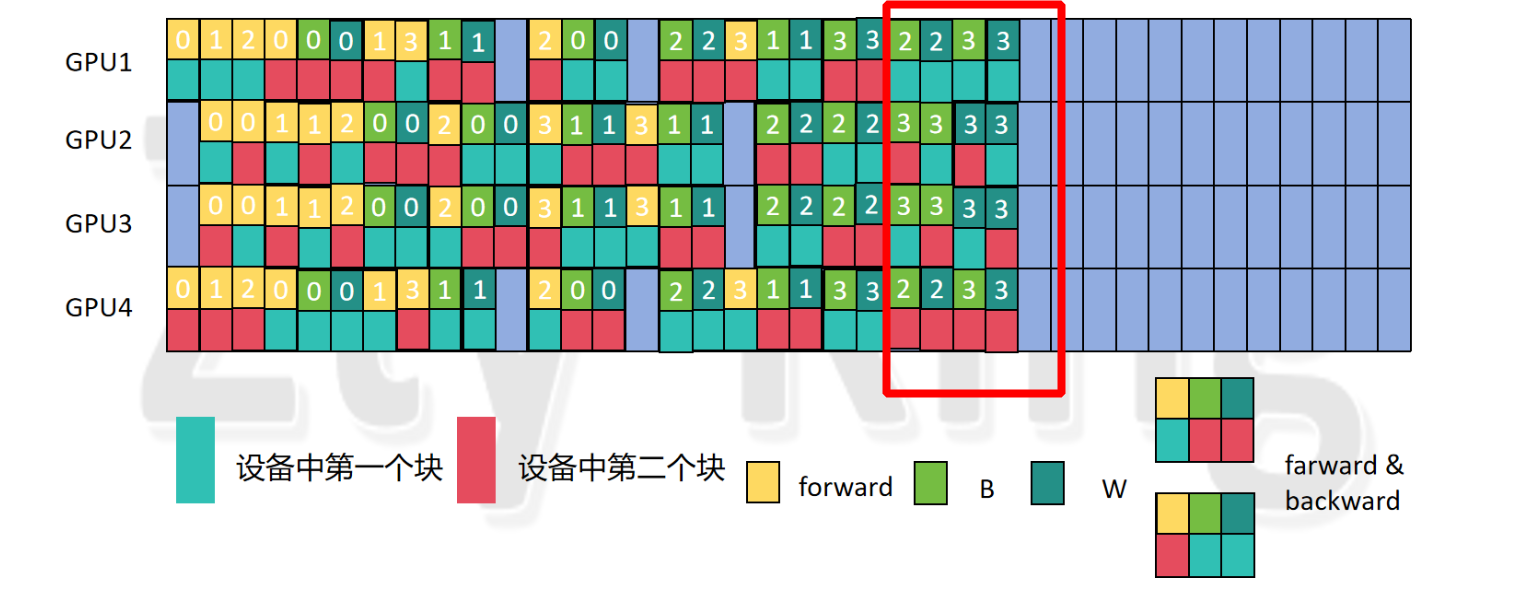
-
在cool_down阶段,假设pp_stage从0开始,
若
pp_stage<pp_degree/2,则,先排pp_stage个,第0块和第1块交替进行(由steady阶段的最后一个backward决定先排哪块的,例如steady阶段的最后一个backward是第0块的,则此时先排第一块的),紧接着排(pp_degree/2-pp_stage)对和W(注意这里的和W并不是一组backward),再排 pp_stage个W(同样是模型块1和2交替排,如果某个模型块W没了,就排另一个)。若
pp_stage>=pp_degree/2,则,将pp_stage替换为pp_degree-pp_stage-1即可。
4.4.2 pp_degree=4,acc_step=6
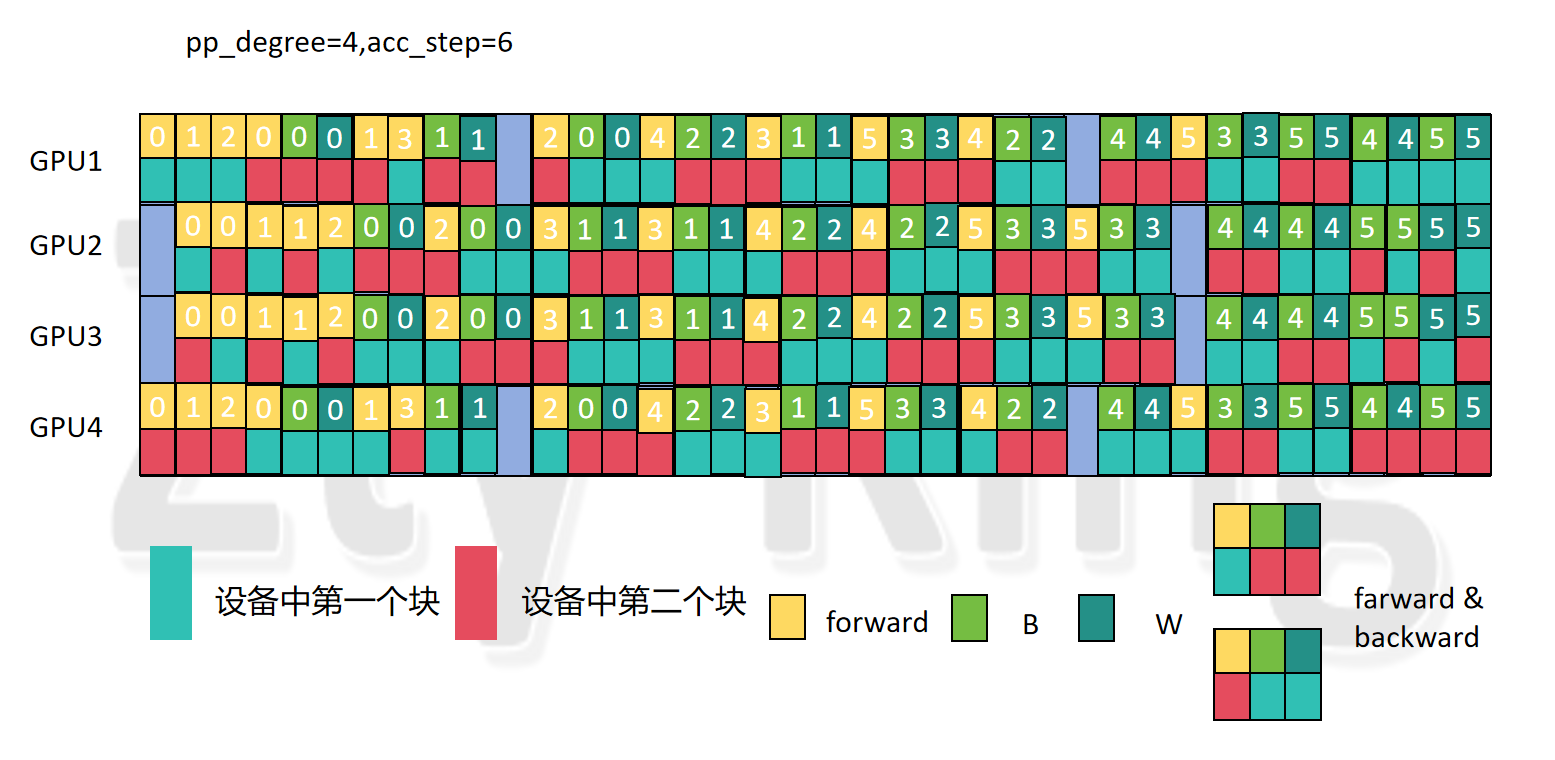
- GPU1 和 GPU 4 有 实际的7个 F & B,GPU 2 和 GPU 3 有 8 个 F & B
- GPU1经过一个 模型块2的1F1B(即F做完,立刻做B)后,再经过一个模型块2的1F,开始做(7+2) 个F&B,并且是两个模型块交替进行,若此��时模型块1的forward部分的micro_batch不够了,则只添加模型块2的backward;GPU4与之刚好相反排列。
- GPU2编排两组两个模型块交替的forward后,开始做(8+2) 个F&B,并且是两个模型块交替进行,若此时模型块1的forward部分的micro_batch不够了,则只添加模型块2的backward,GPU3与之刚好相反排列。
- warm_up阶段和cool_down阶段的步数与 pp_degree=4,acc_step=4 相同。
4.4.3 pp_degree=6,acc_step=6
用5.1.4总结的编排规律计算,做验证:
1.pp_stage: 0
=== Warm-up阶段 === 1.1 5个Forward (模型块0) 1.2 0组双Forward: 1.3 2个Forward-Backward (模型块1) 1.4 1个Forward (模型块1)
=== Steady阶段 === 2.1 Forward & Backward组合:
- 模型块1剩余Forward数: 1
- 模型块2剩余Forward数: 3 2.2 2个只有Backward的步骤
- 最后再排一个backward
=== Cool-down阶段 === 3.1 0个Backward_i (模型块0和1交替) 3.2 3对Backward_i和Weight更新 (模型块0和1交替) 3.3 0个Weight更新 (根据剩余情况在模型块0和1之间交替)
2.pp_stage: 1
=== Warm-up阶段 === 1.1 3个Forward (模型块0) 1.2 1组双Forward:
- Forward (模型块1) + Forward (模型块0) 1.3 1个Forward-Backward (模型块1) 1.4 1个Forward (模型块1)
=== Steady阶段 === 2.1 Forward & Backward组合:
- 模型块1剩余Forward数: 2
- 模型块2剩余Forward数: 3 2.2 2个只有Backward的步骤
- 最后再排一个backward
=== Cool-down阶段 === 3.1 1个Backward_i (模型块0和1交替) 3.2 2对Backward_i和Weight更新 (模型块0和1交替) 3.3 1个Weight更新 (根据剩余情况在模型块0和1之间交替)
3.pp_stage: 2
=== Warm-up阶段 === 1.1 1个Forward (模型块0) 1.2 2组双Forward:
- Forward (模型块1) + Forward (模型块0)
- Forward (模型块1) + Forward (模型块0) 1.3 0个Forward-Backward (模型块1) 1.4 1个Forward (模型块1)
=== Steady阶段 === 2.1 Forward & Backward组合:
- 模型块1剩余Forward数: 3
- 模型块2剩余Forward数: 3 2.2 2个只有Backward的步骤
- 最后再排一个backward
=== Cool-down阶段 === 3.1 2个Backward_i (模型块0和1交替) 3.2 1对Backward_i和Weight更新 (模型块0和1交替) 3.3 2个Weight更新 (根据剩余情况在模型块0和1之间交替)
4.pp_stage: 3
=== Warm-up阶段 === 1.1 1个Forward (模型块1) 1.2 2组双Forward:
- Forward (模型块0) + Forward (模型块1)
- Forward (模型块0) + Forward (模型块1) 1.3 0个Forward-Backward (模型块0) 1.4 1个Forward (模型块0)
=== Steady阶段 === 2.1 Forward & Backward组合:
- 模型块1剩余Forward数: 3
- 模型块2剩余Forward数: 3 2.2 2个只有Backward的步骤
- 最后再排一个backward
=== Cool-down阶段 === 3.1 2个Backward_i (模型块0和1交替) 3.2 1对Backward_i和Weight更新 (模型块0和1交替) 3.3 2个Weight更新 (根据剩余情况在模型块0和1之间交替)
5.pp_stage: 4
=== Warm-up阶段 === 1.1 3个Forward (模型块1) 1.2 1组双Forward:
- Forward (模型块0) + Forward (模型块1) 1.3 1个Forward-Backward (模型块0) 1.4 1个Forward (模型块0)
=== Steady阶段 === 2.1 Forward & Backward组合:
- 模型块1剩余Forward数: 2
- 模型块2剩余Forward数: 3 2.2 2个只有Backward的步骤
- 最后再排一个backward
=== Cool-down阶段 === 3.1 1个Backward_i (模型块0和1交替) 3.2 2对Backward_i和Weight更新 (模型块0和1交替) 3.3 1个Weight更新 (根据剩余情况在模型块0和1之间交替)
6.pp_stage: 5
=== Warm-up阶段 === 1.1 5个Forward (模型块1) 1.2 0组双Forward: 1.3 2个Forward-Backward (模型块0) 1.4 1个Forward (模型块0)
=== Steady阶段 === 2.1 Forward & Backward组合:
- 模型块1剩余Forward数: 1
- 模型块2剩余Forward数: 3 2.2 2个只有Backward的步骤
- 最后再排一个backward
=== Cool-down阶段 === 3.1 0个Backward_i (模型块0和1交替) 3.2 3对Backward_i和Weight更新 (模型块0和1交替) 3.3 0个Weight更新 (根据剩余情况在模型块0和1之间交替)
按照总结的编排流水并行图如下:

可以看到,是完全匹配总结的编排方式的。
4.4.4 总结编排
设置 chunk_flag=(pp_stage // (pp_degree/2)),该变量的值只有0或1
设置 dual_pp_stage=(pp_degree-1)/2)-|pp_stage-((pp_degree-1)/2)|
设置all_step=2*acc_step
**设置F_micro_step_0和F_micro_step_1,B_b_micro_step_0,B_b_micro_step_1,B_w_micro_step_0,B_w_micro_step_1,分别表示模型块0,模型块1的FORWARD,BACKWARD_b,BACKWARD_w的个数,初始值均为0,每编排一个,就加1,当等于all_step时,即表示编排完了 **
排列时都要带上chunk号后缀,F即FORWARD_chunk号,B表示两个即BACKWARD_b_chunk号和BACKWARD_w_chunk号,表示BACKWARD_b_chunk号,W表示BACKWARD_w_chunk号
最终还要加上micro_id后缀,例如在FORWARD_chunk号后加上_id,即FORWARD_chunk号_id,id即对应的micro_step的值
-
warm_up阶段:
先编排pp_degree-(dual_pp_stage +1)-dual_pp_stage ,即(pp_degree-2*dual_pp_stage -2)个模型块 (块号为:chunk_flag)的F,不调整chunk_flag,接着编排(dual_pp_stage+1) 组 1 F(块号为:chunk_flag)1F(模型块号为:(chunk_flag+1)%2,即不同块号的F交替排�列,排列完所有组后,调整一次chunk_flag,即chunk_flag=(chunk_flag+1)%2,再编排(pp_degree/2-dual_pp_stage -1)个1B1F(模型块号为:chunk_flag),记录此时chunk_flag=(chunk_flag+1)%2。
-
steady部分,做的F&B(包括只有backward的部分):
对于模型块1和模型块2计算分别剩余的F,即可组成F&B,
对于模型块1:acc_step-( (pp_degree-2*dual_pp_stage -1)+dual_pp_stage),即 acc_step-(pp_degree-dual_pp_stage-1)
对于模型块2:acc_step-(dual_pp_stage +(pp_degree/2-dual_pp_stage -1)+1)=acc_step - pp_degree/2
对于缺少F的F&B(即只有backward的部分):(pp_degree/2-1)
最后再排一个backward
所以一共为:acc_step-(pp_degree-dual_pp_stage-1)+acc_step - pp_degree/2+(pp_degree/2-1)+1=2*acc_step-pp_degree+dual_pp_stage+1
排列时,排列2*acc_step-pp_degree+dual_pp_stage+1组(F&B),(F的块号与chunk_flag相同,backward与chunk_flag相反,用当前的chunk_flag判断,如chunk_flag此时为1,则此时排的F为FORWARD_1_id0,而B为BACKWARD_b_0_id1,BACKWARD_w_0_id2,也就是要往编排列表里放3个,其中id0就是F_micro_step_1此时的数,相应的id1,id2查B_b_micro_step_0,B_w_micro_step_0的数值即可,0,1分别代表对应的块号),交替排列(即每排一组之后,chunk_flag=(chunk_flag+1)%2),当某个模型块F已经排列完时,直接跳过,此时只排B(即一个BACKWARD_b,BACKWARD_w,块号也用chunk_flag判断,结束后,同样调�整chunk_flag的值,即chunk_flag=(chunk_flag+1)%2 )。
在实际运行过程中,第一个F&B与后面的必须要空(pp_degree/2-1)个bubble
-
cool_down 阶段:
先排dual_pp_stage 个,(由chunk_flag决定块号,0号块和1号块交替排列,同样每排列一个都调整chunk_flag),紧接着排(pp_degree/2-dual_pp_stage )对和W(块号由chunk_flag决定,也按照0,1块号交替排,即每排列一个或者一个W都要更新chunk_flag),再排 dual_pp_stage 个W(块号由chunk_flag决定,同样是模型块1和2交替排,如果某个模型块W没了,即此时B_w_micro_step_0或B_w_micro_step_1等于all_step,就只排另一个不再变换块号)。
6.目前存在的几个疑惑

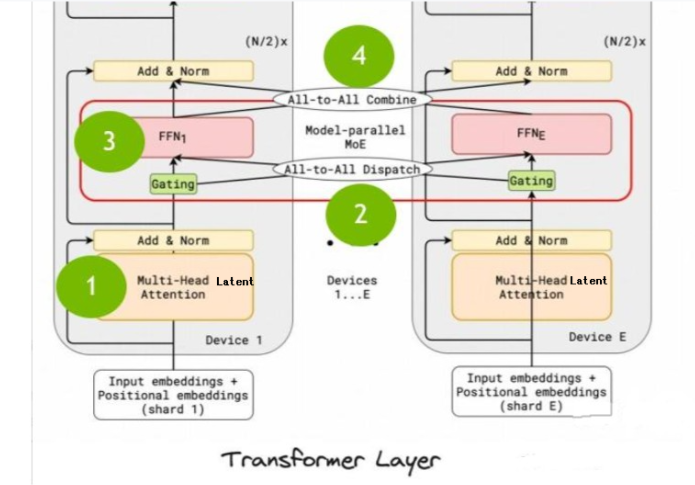
图 6.1
- 如图 6.1所示,核心编排部分(计算与通信重叠),是否是我想的那样,在同一块模型里面有多个block,例如forward,是上一层的forward中的all to all dispatch、MLP、all to all combine与下一层的forward中的attention组合编排,从而达到计算和通信完全重叠。
- 如图 6.1所示,紫色PP部分,是否是在backward之后进行权重梯度同步,例如将设备1上的模型块0的权重与设备7上模型块0的权重梯度同步,如果是,为什么atten(B)和这里的pp通信重叠了,�按道理来说,应该attention(B)计算完,才做梯度同步。
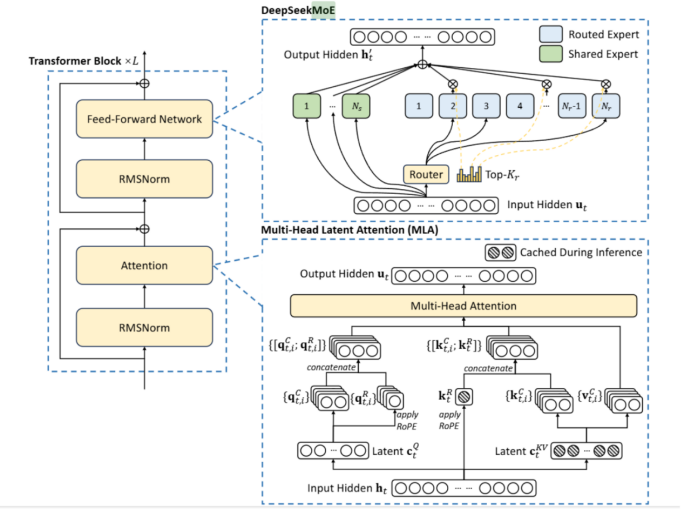
图 6.2
- 如图 6.1所示,在通信和计算重叠的这部分,是把forward和backward又进行了细分,分出了attention,dispatch,mlp,combine,这只是对一个block的切图,如图6.2在开源的model.py代码中是一个block,我们在切图的时候,此时模型块有多个block,如图6.3所示,如果按照vpp的思想是直接整块看成一个整体,但是如果要进行计算和通信重叠的操作,可能需要单独对每一个block切,这时候如果只是直接编排一个forward需要知道此时一个模型块有多少个block,即编排多少组(attention,dispatch,mlp,combine),可能比较麻烦,该如何处理比较好。
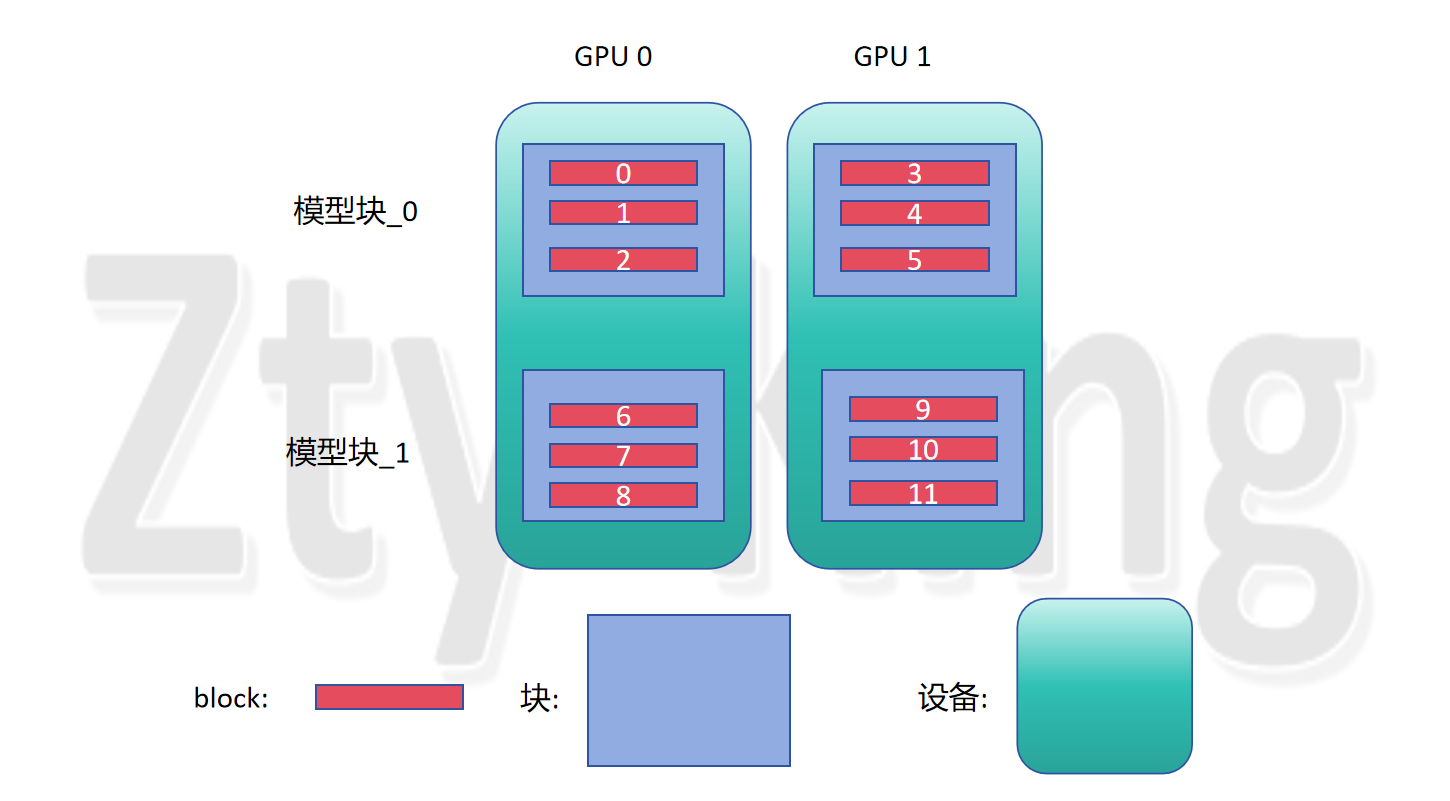
图 6.3
- 每一个block中包含一个MOE,每个MOE包含多个专家,在专家并行时,一般是将一组专家,均匀分到不同的设备上,将专家分到不同设备上这一操作,是否和将模型块均匀分到不同设备上这一操作在同一个地方进行,目前未看到组网,想看看组网的时候dispatch,combine是怎么加进去的。