fused_rotary_position_embedding反向修复

fused_rotary_position_embedding反向修复

fused_rotary_position_embedding API在use_neox_rotary_style为False时，反向传播计算逻辑存在错误。

##Paddle 目前kernel中的反向计算逻辑
def paddle_backward_rotary_pos_emb(dL_dxprime, cos, sin):
    return dL_dxprime * cos - rotate_half(dL_dxprime) * sin

##正确的反向计算逻辑，可以和torch自动微分的结果对齐
def correct_backward_rotary_pos_emb(dL_dxprime, cos, sin):
    return dL_dxprime * cos - rotate_half(dL_dxprime * sin)

paddle kernel代码

template <typename T, typename MPType, int VecSize = 2>
__device__ __forceinline__ void rotate_half(phi::Array<const T*, 3> ins_data,
                                            int num_inputs,
                                            int64_t head_dim,
                                            int64_t index,
                                            int sign,//-1表示反向
                                            MPType* sin_value,
                                            MPType* cos_value,
                                            phi::Array<T*, 3> outs_data) {
  MPType result[VecSize];
  T store[VecSize];
  using VecType = phi::AlignedVector<T, VecSize>;
  constexpr int kVectorsPerThread = VecSize / 2;
  int64_t stride_r = head_dim / 2;
#pragma unroll
  for (int iter = 0; iter < 3; iter++) {
    if (iter >= num_inputs) break;
    // get value_index and rotate_half_index
    int64_t index_v = index;
    int64_t index_r =
        (index % head_dim) < stride_r ? (index + stride_r) : (index - stride_r);
    MPType sign_r = (index % head_dim) < stride_r ? static_cast<MPType>(-1)
                                                  : static_cast<MPType>(1);
    const T* input_v = ins_data[iter] + index_v;
    const T* input_r = ins_data[iter] + index_r;
    VecType* out = reinterpret_cast<VecType*>(outs_data[iter] + index);

#pragma unroll
    for (int nx = 0; nx < VecSize; ++nx) {
      MPType p0 = static_cast<MPType>(input_v[nx]);
      MPType p1 = static_cast<MPType>(input_r[nx]);

      result[nx] = cos_value[nx] * p0 + sign * sign_r * sin_value[nx] * p1;

      store[nx] = static_cast<T>(result[nx]);
    }
    out[0] = *(reinterpret_cast<VecType*>(store));
  }
}

复现代码

import paddle
import torch
import numpy as np
import unittest

from paddle.utils import map_structure

try:
    from paddle.fluid.framework import in_dygraph_mode
except:
    from paddle.base.framework import in_dygraph_mode
TOLERANCE = {
    "float32": {"atol": 1e-6, "rtol": 1e-6},
    "float16": {"atol": 1e-3, "rtol": 1e-3},
    "bfloat16": {"atol": 1e-2, "rtol": 1e-2},
}

'''
TOLERANCE = {
    "float32": {"atol": 0, "rtol": 1e-6},
    "float16": {"atol": 0, "rtol": 1e-5},
    "bfloat16": {"atol": 0, "rtol": 1e-5},
}
'''


def convert_dtype_to_torch_type(dtype):
    import torch

    if dtype in ["float32", np.float32]:
        return torch.float32
    elif dtype in ['float16', np.float16]:
        return torch.float16
    elif dtype in ['bfloat16', np.uint16]:
        return torch.bfloat16
    elif dtype in ['uint8', np.uint8]:
        return torch.uint8
    elif dtype in ['int32', np.int32]:
        return torch.int32
    elif dtype in ['int64', np.int64]:
        return torch.int64
    elif dtype in ['bool']:
        return torch.bool
    elif dtype in ['complex64', np.complex64]:
        return torch.complex64
    else:
        raise ValueError(f'Unsupport dtype: {dtype}')


def grad(outputs, inputs, grad_outputs=None, no_grad_vars=None):
    if in_dygraph_mode():
        return paddle.grad(outputs, inputs, grad_outputs=grad_outputs, no_grad_vars=no_grad_vars)
    else:
        return paddle.static.gradients(outputs, inputs, target_gradients=grad_outputs, no_grad_set=no_grad_vars)
    
def np_assert_accuracy(
    np_a,
    np_b,
    atol,
    rtol,
    dtype,
    version_a,
    version_b,
    eager_or_static_mode,
    fwd_or_bkd,
    api,
):  
    max_atol_idx = np.argmax(np.abs(np_a - np_b))
    np_a_flatten = np_a.flatten()
    np_b_flatten = np_b.flatten()
    sub_res = np_a_flatten - np_b_flatten
    nonzero_idx = np.nonzero(np_b_flatten)
    sub_res = sub_res.take(nonzero_idx)
    np_b_flatten_nonzero = np_b_flatten.take(nonzero_idx).flatten()
    np_a_flatten_nonzero = np_a_flatten.take(nonzero_idx).flatten()
    if sub_res.size ==0:
        max_rtol_idx = 0
    else:
        max_rtol_idx = np.argmax(np.abs(sub_res / np_b_flatten_nonzero))
    np.testing.assert_allclose(
        np_a,
        np_b,
        rtol,
        atol,
        err_msg=(
            '{api} {eager_or_static_mode} {fwd_or_bkd}: compare {version_a} res with {version_b} failed in {dtype} dtype,\n'.format(
                api=api,
                eager_or_static_mode=eager_or_static_mode,
                fwd_or_bkd=fwd_or_bkd,
                version_a=version_a,
                version_b=version_b,
                dtype=dtype,
            )
            + 'max_atol value, {version_a}_value: {value_a}, {version_b}_value: {value_b},\n'.format(
                version_a=version_a,
                value_a=str(np_a_flatten[max_atol_idx].item()),
                version_b=version_b,
                value_b=str(np_b_flatten[max_atol_idx].item()),
            )
            + 'max_rtol value , {version_a}_value: {value_a}, {version_b}_value: {value_b},\n'.format(
                version_a=version_a,
                value_a=str(np_a_flatten_nonzero[max_rtol_idx].item()) if max_rtol_idx < len(np_a_flatten_nonzero) else '',
                version_b=version_b,
                value_b=str(np_b_flatten_nonzero[max_rtol_idx].item()) if max_rtol_idx < len(np_b_flatten_nonzero) else '',
            )
        ),
    )


def np_assert_staility(
    np_actual,
    np_baseline,
    dtype,
    version,
    eager_or_static_mode,
    fwd_or_bkd,
    api,
):
    max_atol_idx = np.argmax(np.abs(np_actual - np_baseline))
    np_actual_flatten = np_actual.flatten()
    np_baseline_flatten = np_baseline.flatten()
    sub_res = np_actual_flatten - np_baseline_flatten
    nonzero_idx = np.nonzero(np_baseline_flatten)
    sub_res = sub_res.take(nonzero_idx)
    np_baseline_flatten_nonzero = np_baseline_flatten.take(nonzero_idx).flatten()
    if sub_res.size == 0:
        max_rtol_idx = 0
    else:
        np_actual_flatten_nonzero = np_actual_flatten.take(nonzero_idx).flatten()
        max_rtol_idx = np.argmax(np.abs(sub_res / np_baseline_flatten_nonzero))
    np.testing.assert_equal(
        np_actual,
        np_baseline,
        err_msg=(
            '{eager_or_static_mode} {fwd_or_bkd}: {version} is unstable in {dtype} dtype,\n'.format(
                eager_or_static_mode=eager_or_static_mode,
                fwd_or_bkd=fwd_or_bkd,
                version=version,
                dtype=dtype,
            )
            + 'max_atol value, {version}_value: {actual_value}, {version}_baseline_value: {baseline_value}, \n'.format(
                version=version,
                actual_value=str(np_actual_flatten[max_atol_idx].item()),
                baseline_value=str(np_baseline_flatten[max_atol_idx].item()),
            )
            + 'max_rtol value,  {version}_value: {actual_value}, {version}_baseline_value: {baseline_value}, \n'.format(
                version=version,
                actual_value=str(np_actual_flatten_nonzero[max_rtol_idx].item()),
                baseline_value=str(np_baseline_flatten_nonzero[max_rtol_idx].item()),
            )
        ),
    )

def rotate_half(x):
    x1, x2 = x.chunk(2, dim=-1)
    return torch.cat((-x2, x1), dim=-1)

## half模式下前向计算逻辑
def apply_rotary_pos_emb(x, cos, sin):
    return x * cos + rotate_half(x) * sin
    
##Paddle 目前kernel中的反向计算逻辑
def paddle_backward_rotary_pos_emb(dL_dxprime, cos, sin):
    return dL_dxprime * cos - rotate_half(dL_dxprime) * sin

##正确的反向计算逻辑，可以和torch自动微分的结果对齐
def correct_backward_rotary_pos_emb(dL_dxprime, cos, sin):
    return dL_dxprime * cos - rotate_half(dL_dxprime * sin)


from typing import Optional
def torch_fused_rotary_position_embedding2(
    q: torch.Tensor,
    k: Optional[torch.Tensor] = None,
    v: Optional[torch.Tensor] = None,
    sin: Optional[torch.Tensor] = None,
    cos: Optional[torch.Tensor] = None,
    position_ids: Optional[torch.Tensor] = None,
    use_neox_rotary_style: bool = True,
    time_major: bool = False,
    rotary_emb_base: float = 10000.0,
) -> tuple[torch.Tensor, Optional[torch.Tensor], Optional[torch.Tensor]]:
    qn = apply_rotary_pos_emb(q,cos,sin)
    kn = apply_rotary_pos_emb(k,cos,sin)
    vn = apply_rotary_pos_emb(v,cos,sin)
    return qn, kn, vn

 
def torch_fused_rotary_position_embedding(
    q: torch.Tensor,
    k: Optional[torch.Tensor] = None,
    v: Optional[torch.Tensor] = None,
    sin: Optional[torch.Tensor] = None,
    cos: Optional[torch.Tensor] = None,
    position_ids: Optional[torch.Tensor] = None,
    use_neox_rotary_style: bool = True,
    time_major: bool = False,
    rotary_emb_base: float = 10000.0,
) -> tuple[torch.Tensor, Optional[torch.Tensor], Optional[torch.Tensor]]:

    from typing import Optional

    def _deal_qkv_pytorch(init_value: Optional[torch.Tensor]) -> Optional[torch.Tensor]:
        if init_value is None:
            return None
        return init_value.permute(0, 2, 1, 3)

    def _mult_qkv_pytorch(
        value: Optional[torch.Tensor],
        cos_tensor: torch.Tensor,
        sin_tensor: torch.Tensor,
    ) -> Optional[torch.Tensor]:
        if value is None:
            return None
        rotate_half_q = torch.stack([-value[..., 1::2], value[..., 0::2]], dim=-1).reshape(value.shape)
        query = value * cos_tensor + rotate_half_q * sin_tensor
        return query

    def _mult_qkv_rotate_half_pytorch(
        value: Optional[torch.Tensor],
        cos_tensor: torch.Tensor,
        sin_tensor: torch.Tensor,
    ) -> Optional[torch.Tensor]:
        if value is None:
            return None
        head_dim = value.shape[-1]
        half_dim = head_dim // 2
        rotate_half_q = torch.cat([-value[..., half_dim:], value[..., :half_dim]], dim=-1)
        query = value * cos_tensor + rotate_half_q * sin_tensor
        return query

    def _get_sin_cos_tensor_pytorch(
        seq_len: int, head_dim: int, sign: int = 1, rotate_half: bool = False
    ):
        pos_seq = torch.arange(0, seq_len, 1, dtype=torch.float32)
        indices = torch.arange(0, head_dim, 2, dtype=torch.float32)
        indices = 1 / (rotary_emb_base ** (indices / head_dim))
        sinusoid_inp = pos_seq.unsqueeze(1) * indices.unsqueeze(0)
        sinusoid_inp = sinusoid_inp.unsqueeze(0).unsqueeze(2)

        sin_tensor = torch.zeros(1, seq_len, 1, head_dim, dtype=torch.float32)
        cos_tensor = torch.zeros(1, seq_len, 1, head_dim, dtype=torch.float32)

        if rotate_half:
            stride = head_dim // 2
            sin_tensor[..., :stride] = sign * torch.sin(sinusoid_inp)
            sin_tensor[..., stride:] = torch.sin(sinusoid_inp)
            cos_tensor[..., :stride] = torch.cos(sinusoid_inp)
            cos_tensor[..., stride:] = torch.cos(sinusoid_inp)
        else:
            sin_tensor[..., 0::2] = sign * torch.sin(sinusoid_inp)
            sin_tensor[..., 1::2] = torch.sin(sinusoid_inp)
            cos_tensor[..., 0::2] = torch.cos(sinusoid_inp)
            cos_tensor[..., 1::2] = torch.cos(sinusoid_inp)

        return sin_tensor, cos_tensor

    init_q, init_k, init_v = q, k, v
    if time_major:
        init_q = init_q.permute(1, 0, 2, 3)
        if init_k is not None:
            init_k = init_k.permute(1, 0, 2, 3)
        if init_v is not None:
            init_v = init_v.permute(1, 0, 2, 3)

    head_dim = init_q.shape[3]
    seq_len = init_q.shape[1]

    sin_tensor, cos_tensor = sin, cos
    if sin_tensor is None or cos_tensor is None:
        sin_tensor, cos_tensor = _get_sin_cos_tensor_pytorch(seq_len, head_dim, rotate_half=not use_neox_rotary_style)
        sin_tensor = sin_tensor.to(dtype=q.dtype, device=q.device)
        cos_tensor = cos_tensor.to(dtype=q.dtype, device=q.device)

    q_rope = _deal_qkv_pytorch(init_q)
    k_rope = _deal_qkv_pytorch(init_k)
    v_rope = _deal_qkv_pytorch(init_v)
    print(sin_tensor.shape)
    if position_ids is not None:
        print(position_ids)
        sin_tensor = sin_tensor.squeeze((0, 2))[position_ids].unsqueeze(2)
        cos_tensor = cos_tensor.squeeze((0, 2))[position_ids].unsqueeze(2)

    sin_tensor = sin_tensor.permute(0, 2, 1, 3)
    cos_tensor = cos_tensor.permute(0, 2, 1, 3)

    if use_neox_rotary_style:
        query = _mult_qkv_pytorch(q_rope, cos_tensor, sin_tensor)
        value = _mult_qkv_pytorch(v_rope, cos_tensor, sin_tensor)
        key = _mult_qkv_pytorch(k_rope, cos_tensor, sin_tensor)
    else:
        query = _mult_qkv_rotate_half_pytorch(q_rope, cos_tensor, sin_tensor)
        value = _mult_qkv_rotate_half_pytorch(v_rope, cos_tensor, sin_tensor)
        key = _mult_qkv_rotate_half_pytorch(k_rope, cos_tensor, sin_tensor)

    r_query = _deal_qkv_pytorch(query)
    r_key = _deal_qkv_pytorch(key)
    r_value = _deal_qkv_pytorch(value)

    if time_major:
        r_query = r_query.permute(1, 0, 2, 3)
        if r_key is not None:
            r_key = r_key.permute(1, 0, 2, 3)
        if r_value is not None:
            r_value = r_value.permute(1, 0, 2, 3)

    return r_query, r_key, r_value


def print_matrix(name, arr, precision=5):
    import numpy as np
    np.set_printoptions(precision=precision, suppress=True)
    print(f"{name}:\n{arr}\n")


class TestFusedRotatryPositionEmbeddingCase1(unittest.TestCase):
    def setUp(self):
        self.init_params()
        self.init_threshold()
        self.init_shape()
        self.generate_np_inputs_and_dout()
        q_torch, k_torch, v_torch, sin_torch, cos_torch, position_id_torch, dq_torch, dk_torch, dv_torch = self.gen_torch_inputs_and_dout()
        q_torch,k_torch,v_torch, torch_out_grads = self.cal_torch_res(
            q_torch, k_torch, v_torch, sin_torch, cos_torch, position_id_torch, dq_torch, dk_torch, dv_torch
        )
        self.q_torch = q_torch.cpu().detach().numpy()
        self.k_torch = k_torch.cpu().detach().numpy()
        self.v_torch = v_torch.cpu().detach().numpy()
        self.out_grads_torch = map_structure(
            lambda x: x.cpu().detach().numpy(),
            torch_out_grads,
        )
        torch.cuda.empty_cache()

    def generate_np_inputs_and_dout(self):
        self.q_np = np.random.random(size=self.q_shape).astype("float32")
        self.k_np = np.random.random(size=self.q_shape).astype("float32")
        self.v_np = np.random.random(size=self.q_shape).astype("float32")
        self.sin_np = np.random.random(size=self.sin_shape).astype("float32")

        self.cos_np = np.random.random(size=self.sin_shape).astype("float32")
        self.position_id_np = np.array([[0, 1, 2, 3, 4, 5, 6, 7]]).astype("int64")
        self.dq_np = np.random.random(size=self.q_shape).astype("float32")
        self.dk_np = np.random.random(size=self.q_shape).astype("float32")
        self.dv_np = np.random.random(size=self.q_shape).astype("float32")

    def init_params(self):
        self.q_dtype = "float32"
        self.pos_dtype = "int64"
        
    def init_threshold(self):
        self.atol = TOLERANCE["float32"]["atol"]
        self.rtol = TOLERANCE["float32"]["rtol"]

    def init_shape(self):
        self.q_shape = [1,8, 2, 8]
        self.sin_shape = [1, 8, 1, 8]
        pass

    def gen_torch_inputs_and_dout(self):
       
        q_torch = torch.tensor(self.q_np,device='cuda',requires_grad=True,dtype=convert_dtype_to_torch_type(self.q_dtype))
        k_torch = torch.tensor(self.k_np,device='cuda',requires_grad=True,dtype=convert_dtype_to_torch_type(self.q_dtype))
        v_torch = torch.tensor(self.v_np,device='cuda',requires_grad=True,dtype=convert_dtype_to_torch_type(self.q_dtype))
        sin_torch = torch.tensor(self.sin_np,device='cuda',requires_grad=False,dtype=convert_dtype_to_torch_type(self.q_dtype))
        print(sin_torch)
       
        cos_torch = torch.tensor(self.cos_np,device='cuda',requires_grad=False,dtype=convert_dtype_to_torch_type(self.q_dtype))
        print(cos_torch)
        position_id_torch = torch.tensor(self.position_id_np,device='cuda',requires_grad=False,dtype=convert_dtype_to_torch_type(self.pos_dtype))
        
        dq_torch = torch.tensor(self.dq_np,device='cuda',requires_grad=False,dtype=convert_dtype_to_torch_type(self.q_dtype))
        dk_torch = torch.tensor(self.dk_np,device='cuda',requires_grad=False,dtype=convert_dtype_to_torch_type(self.q_dtype))
        dv_torch = torch.tensor(self.dv_np,device='cuda',requires_grad=False,dtype=convert_dtype_to_torch_type(self.q_dtype))
            
        return q_torch, k_torch, v_torch, sin_torch, cos_torch, position_id_torch, dq_torch, dk_torch, dv_torch

    def gen_eager_inputs_and_dout(self):
        
        q_eager = paddle.to_tensor(self.q_np,dtype=self.q_dtype)
        k_eager = paddle.to_tensor(self.k_np,dtype=self.q_dtype)
        v_eager = paddle.to_tensor(self.v_np,dtype=self.q_dtype)
        sin_eager = paddle.to_tensor(self.sin_np,dtype=self.q_dtype)
        cos_eager = paddle.to_tensor(self.cos_np,dtype=self.q_dtype)
        position_id_eager = paddle.to_tensor(self.position_id_np,dtype=self.pos_dtype)
        dq_eager = paddle.to_tensor(self.dq_np,dtype=self.q_dtype)
        dk_eager = paddle.to_tensor(self.dk_np,dtype=self.q_dtype)
        dv_eager = paddle.to_tensor(self.dv_np,dtype=self.q_dtype)
        q_eager.stop_gradient = False
        k_eager.stop_gradient = False
        v_eager.stop_gradient = False

        return q_eager, k_eager, v_eager, sin_eager, cos_eager, position_id_eager, dq_eager, dk_eager, dv_eager

    def cal_torch_res(self,q_torch, k_torch, v_torch, sin_torch, cos_torch, position_id_torch, dq_torch, dk_torch, dv_torch):
        q,k,v = torch_fused_rotary_position_embedding2(q_torch, k_torch, v_torch, sin_torch, cos_torch, position_id_torch,False,False)
        out_grads = torch.autograd.grad([q,k,v], [q_torch, k_torch, v_torch], grad_outputs=[dq_torch, dk_torch, dv_torch])
        return q,k,v, out_grads

    def cal_eager_res(self,q_eager,k_eager,v_eager,sin_eager, cos_eager, position_id_eager, dq_eager, dk_eager, dv_eager):
        q,k,v = paddle.incubate.nn.functional.fused_rotary_position_embedding(q_eager,k_eager,v_eager,sin_eager, cos_eager, position_id_eager,False,False)
        out_grads = paddle.grad([q,k,v], [q_eager,k_eager,v_eager], grad_outputs=[dq_eager, dk_eager, dv_eager])
        return q,k,v, out_grads

    def test_eager_accuracy(self):
        q_eager, k_eager, v_eager, sin_eager, cos_eager, position_id_eager, dq_eager, dk_eager, dv_eager= self.gen_eager_inputs_and_dout()
        paddle_q, paddle_k, paddle_v, paddle_out_grads= self.cal_eager_res(
            q_eager, k_eager, v_eager, sin_eager, cos_eager, position_id_eager, dq_eager, dk_eager, dv_eager
        )
       
        paddle.device.cuda.empty_cache()
        out_grads_eager_np = map_structure(
            lambda x: x.numpy(),
            paddle_out_grads,
        )

       
        np_assert_accuracy(
            paddle_q.numpy(),
            self.q_torch,
            self.atol,
            self.rtol,
            self.q_dtype,
            version_a="paddle_develop",
            version_b="torch",
            eager_or_static_mode="eager",
            fwd_or_bkd="forward",
            api="paddle.fused_rotary_position_embedding",
        )
       
        np_assert_accuracy(
            paddle_k.numpy(),
            self.k_torch,
            self.atol,
            self.rtol,
            self.q_dtype,
            version_a="paddle_develop",
            version_b="torch",
            eager_or_static_mode="eager",
            fwd_or_bkd="forward",
            api="paddle.fused_rotary_position_embedding",
        )
      
        np_assert_accuracy(
            paddle_v.numpy(),
            self.v_torch,
            self.atol,
            self.rtol,
            self.q_dtype,
            version_a="paddle_develop",
            version_b="torch",
            eager_or_static_mode="eager",
            fwd_or_bkd="forward",
            api="paddle.fused_rotary_position_embedding",
        )

        for idx in range(len(out_grads_eager_np)):
            np_assert_accuracy(
                
                out_grads_eager_np[idx],
                self.out_grads_torch[idx],
                self.atol,
                self.rtol,
                self.q_dtype,
                version_a="paddle_develop",
                version_b="torch",
                eager_or_static_mode="eager",
                fwd_or_bkd="backward",
                api="paddle._C_ops.embedding",
            )

if __name__ == '__main__':
    seed = 2025
    torch.manual_seed(seed)
    torch.cuda.manual_seed(seed)
    paddle.seed(seed)
    np.random.seed(seed)
    unittest.main()

解决思路：

1.解决方法

结论：需要把“sin 的逐元素乘”放进旋转里用到的那一侧（配对维度）的 sin。最小改法是在发射 kernel 的地方，反向时改用“配对索引”的 sin 缓存再调用现有的 rotate_half，这样无需改 rotate_half 签名。

建议改动点（思路）：

• 文件：paddle/paddle/phi/kernels/fusion/gpu/fused_rope_utils.h
• 位置：VectorizedFusedRopeWithRotateHalfKernel(...) 内，每次循环里我们现在这样做： 1) 先用 VectorizedGetSinCos::run(..., index, ..., sin_value, cos_value) 得到当前位置 index 的 sin_value/cos_value 2) 直接调用 rotate_half(ins_data, ..., sign, sin_value, cos_value, outs_data)
• 修改为（仅当 sign==-1，即反向）： 1) 仍然先算当前位置的 cos_value（保留） 2) 再额外用“配对基址”计算一份“旋转后位置”的 sin：令
  • stride_r = head_dim / 2
  • index_r_base = ((index % head_dim) < stride_r) ? (index + stride_r) : (index - stride_r)
  • 调用 VectorizedGetSinCos::run(..., index_r_base, ..., sin_value, /*cos可忽略*/) 重算 sin 到同一个 sin_value 缓存里 3) 然后调用原来的 rotate_half(...)。这样在反向路径中，rotate_half(dL_dxprime) 里乘到的就是“配对维度的 sin”，实现等价于 -R(dL_dxprime ⊙ sin)，从而得到 dL/dx = dL/dx' ⊙ cos − R(dL/dx' ⊙ sin)

要点：

• 前向（sign==+1）保持不变，沿用当前位置 sin_value；
• 反向（sign==-1）在调用 rotate_half 前把 sin_value 换成配对位置的那份；
• 两个分支（默认 rotary_base=kDefaultRotaryBase 与通用分支）都要做同样处理；
• 这是最小侵入改法，不改 rotate_half 签名；如果愿意改签名，也可以给 rotate_half 增参 sin_value_rot，在 sign==-1 时用 sin_value_rot[nx] 代替 sin_value[nx]。

这样就把实际实现从

• 旧：grad_x = g * cos - rotate_half(g) * sin 改为
• 新：grad_x = g * cos - rotate_half(g * sin)，严格对齐数学推导与 PyTorch 自动微分。

2.详细解释

• 原来的 sin_value 是什么

  • 在 kernel 里，VectorizedGetSinCos::run(...) 用“当前元素索引 index”计算出的 sin_value[nx] 与 cos_value[nx]。也就是当前半维位置的 sin/cos，而不是“与之成对的另一半维”的 sin/cos。
  • 随后 rotate_half(...) 内会取
    • p0 = 当前半维的数据（或上游梯度 g0）
    • p1 = 成对半维的数据（或上游梯度 g1，对应 index_r）
    • 计算式：result[nx] = cos_value[nx] * p0 + sign * sign_r * sin_value[nx] * p1

• 为啥这会导致反向里“乘 sin 的位置不对”

  • 正确的反向公式：设上游梯度 g，R=rotate_half，则
    • y = x⊙cos + R(x)⊙sin
    • dL/dx = g⊙cos − R(g⊙sin)
  • 展开到每对二维（x0,x1）：
    • 正确：dx0 = g0c0 + g1s1；dx1 = g1c1 − g0s0
  • 旧实现做的是：dx = g⊙cos − R(g)⊙sin
    • 展开：dx0 = g0c0 + g1s0；dx1 = g1c1 − g0s1
    • 可见，乘 sin 的那一项，应该是“配对维度的 sin”（s1/s0），而旧实现用的是“当前维度的 sin”（s0/s1），两者在一般情况下不相等（只有当一对维度的 sin 完全相同才凑巧一致）。

• 为什么“把 sin_value 改为配对索引的 sin”就对了

  • 在 rotate_half(...) 中，p1 取自“配对半维”（index_r），而 sin 还用的是“当前半维”的 sin。这等价于 R(g) 后再逐元素乘 sin（即错位乘）。
  • 我们在进入 rotate_half 前，若是反向（sign == -1），先把 sin_value 改成“配对半维”的 sin（用 get_paired_sin_values 取到 pos_head_r 的 sin），这样 sin_value[nx] * p1 实际就是“配对分量的 sin 与配对分量的 g 相乘”，实现的就是 R(g⊙sin) 中那一项。
  • 于是整体变为：dL/dx = g⊙cos − rotate_half(g⊙sin)，与数学推导严格一致。

• 为啥不用改 cos

  • 正确公式里的 cos 项是 g⊙cos，逐元素与“当前分量”相乘即可，不涉及配对交换，所以保持 cos_value 按当前索引即可。

• 小结

  • 原本：sin_value 对应“当前半维”，但在 rotate_half 里与“配对半维的数据 p1”相乘，导致计算变成 g⊙cos − R(g)⊙sin。
  • 修改：在反向时，把 sin_value 换成“配对半维的 sin”，让 sin_value[nx] * p1 变成“配对分量 g1 与其对应的 sin1 相乘”，等价实现 g⊙cos − R(g⊙sin)。
  • 这就是为什么“把 sin_value 换成配对索引的 sin”就对了的原因。

3.求导过程

回顾问题设置：

假设我们有一个二维向量 v = (x, y) ，首先进行旋转，得到新的向量 v'，然后将其每个分量按元素乘以 sin(θ)，得到最终结果v''。

1. 旋转操作：

首先，旋转V $$ \mathbf{v'} = R \cdot \mathbf{v} = (-y, x) $$

2. 按元素乘以 sin(θ)

然后，按元素乘以 sin(θ)： $$ \mathbf{v''} = \mathbf{v'} \cdot \sin(\theta) = (-y \sin(\theta), x \sin(\theta)) $$

梯度计算

假设我们要计算损失函数 ( L ) 相对于 $\mathbf{v} $ 的梯度，使用链式法则： $$ \frac{\partial L}{\partial \mathbf{v}} = \frac{\partial L}{\partial \mathbf{v''}} \cdot \frac{\partial \mathbf{v''}}{\partial \mathbf{v}} $$

1. 计算 ( \mathbf{v''} ) 对 ( \mathbf{v'} ) 的梯度

首先，计算 v''对 v'的梯度： $$ \frac{\partial \mathbf{v''}}{\partial \mathbf{v'}} = \begin{pmatrix} \frac{\partial (-y \sin(\theta))}{\partial (-y)} & 0 \ 0 & \frac{\partial (x \sin(\theta))}{\partial x} \end{pmatrix} = \begin{pmatrix} \sin(\theta) & 0 \ 0 & \sin(\theta) \end{pmatrix} $$ 这表示 v''每个分量的变化都与sin(θ)成正比。

2. 计算 v'对 v的梯度

然后，计算v'对v的梯度： $$ \frac{\partial \mathbf{v'}}{\partial \mathbf{v}} = \begin{pmatrix} 0 & -1 \ 1 & 0 \end{pmatrix} $$ 这是因为旋转操作是线性的，分别是 ( x ) 和 ( y ) 对应的变换。

正向的时候，是一个逆时针旋转的矩阵： $$ R = \begin{pmatrix} 0 & 1 \ -1 & 0 \end{pmatrix} $$

3. 链式法则求梯度

现在，可以通过链式法则计算总的梯度： $$ \frac{\partial L}{\partial \mathbf{v}} = \frac{\partial L}{\partial \mathbf{v''}} \cdot \frac{\partial \mathbf{v''}}{\partial \mathbf{v'}} \cdot \frac{\partial \mathbf{v'}}{\partial \mathbf{v}} $$

其中，注意到在链式法则中，梯度传播的顺序很重要。在每个步骤中，sin(θ)会“携带”在旋转的梯度中，所以每个梯度的传播都需要包含sin(θ)。

4.为什么之前的单测能正常运行

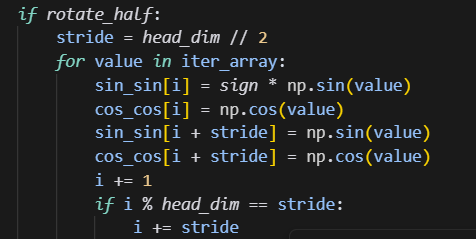
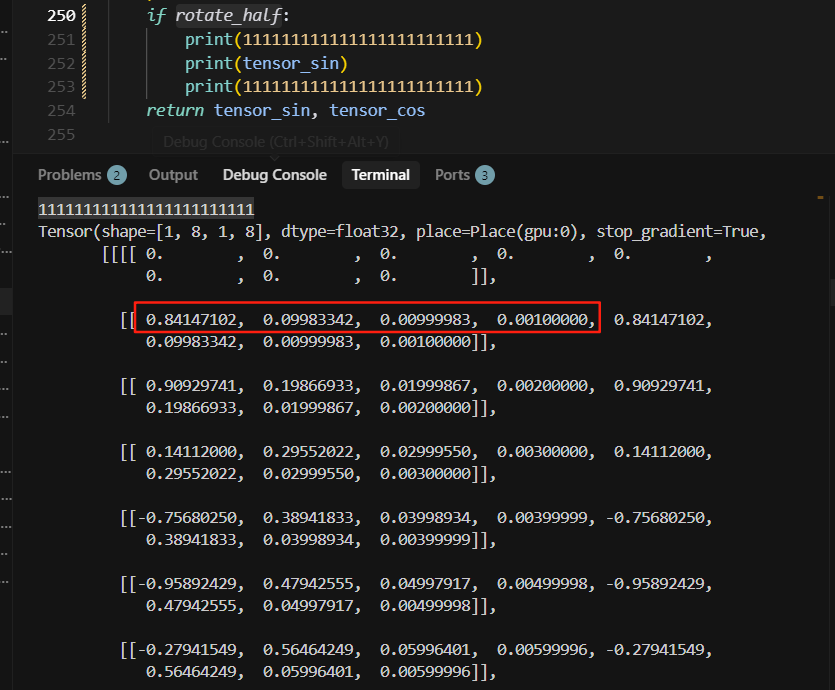
rotate_half为True时，正确的计算顺序如下：

而实际计算顺序是：

但是旧的单测，rotate_half为True时，前半部分的sin数据和后半部分的sin数据是一致的，此时s1和s0二者相等，所以跑出来的数据也相等了。

验证事实性：

修改如下：

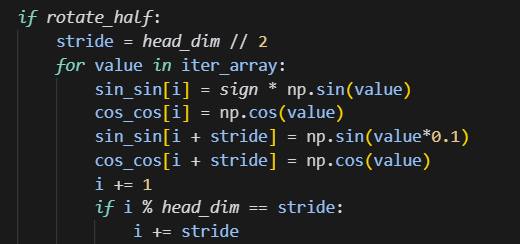
原来的逻辑测试结果：

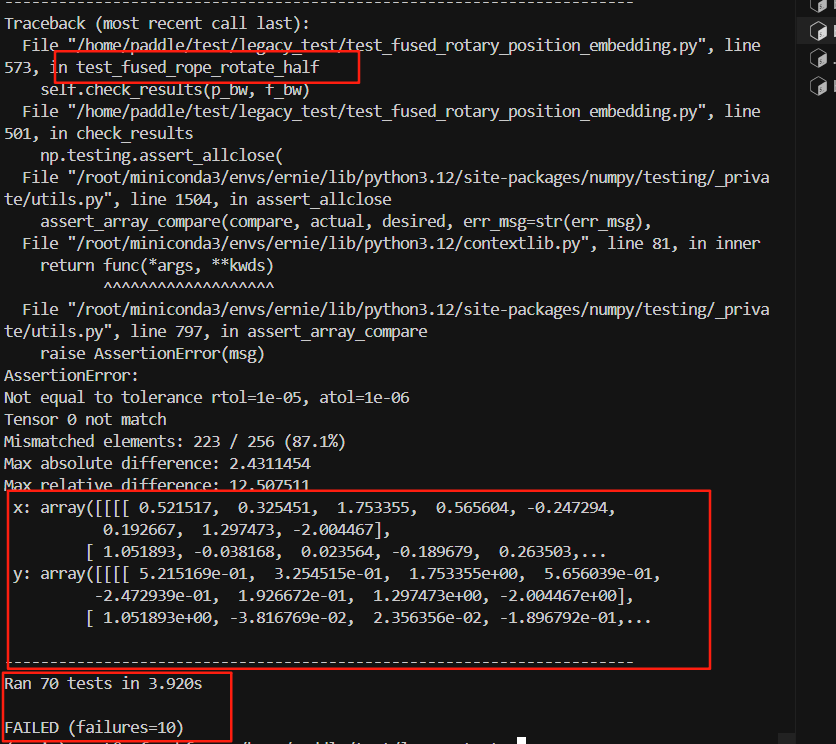
现在的逻辑测试结果：