Skip to main content

Vpp去尾工作

1.检查当前是否支持模型层数为（vpp_degree*pp_degree-1）​

1.1 追溯报错源头​

运行参数为vpp_degree=2,pp_degree=2,hidden_layer=7

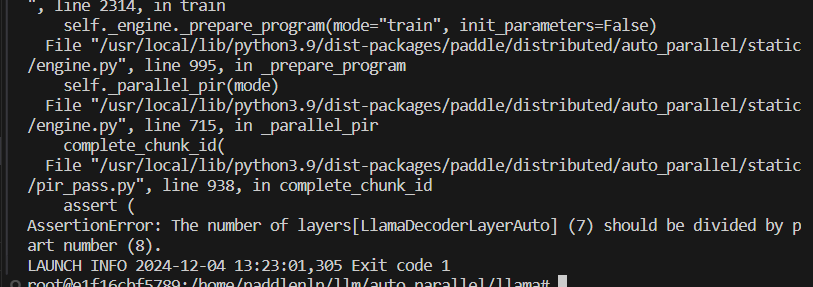
image-20241204212515783

报错，有assert检查，追溯相关代码，

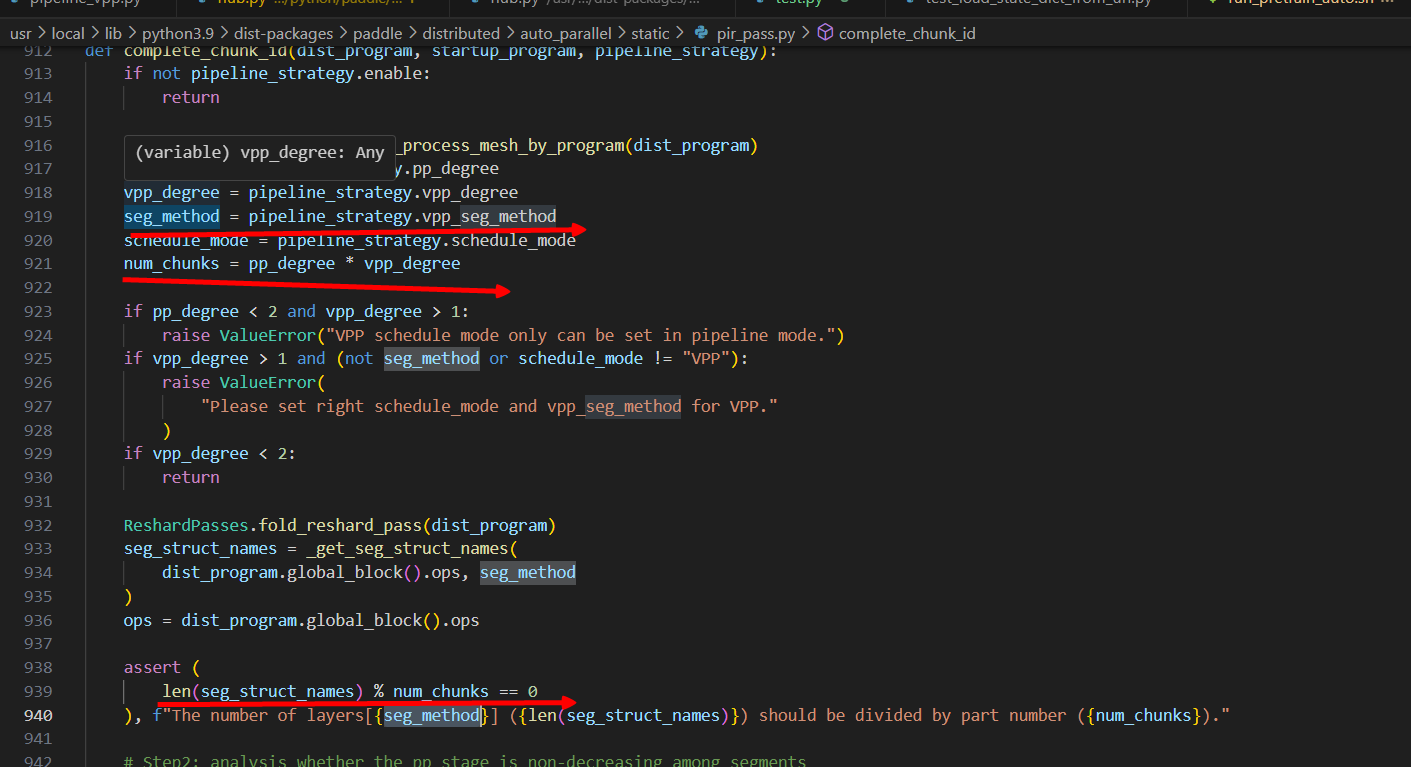
image-20241204212755148

可以看到，这里做了一个判断，即切分结构名称的个数必须是num_chunks的整数倍，同时发现一些定义，切分方式、切分结构名称等

2.运行参数为vpp_degree=2,pp_degree=2,hidden_layer=8，进行追溯​

2.1 追溯seg_method​

先追溯seg_method

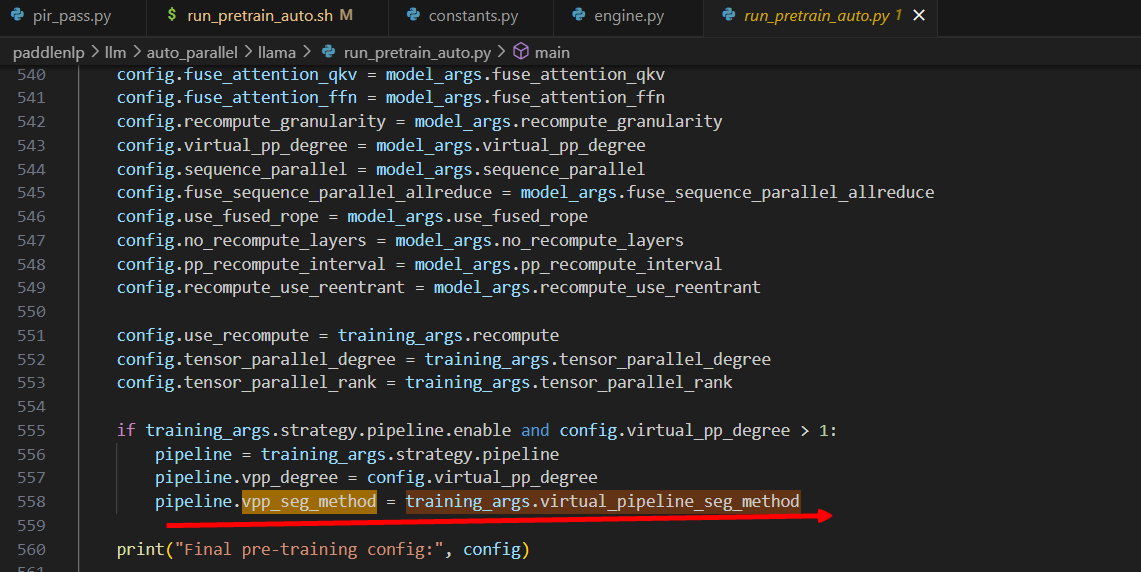
image-20241204213921661

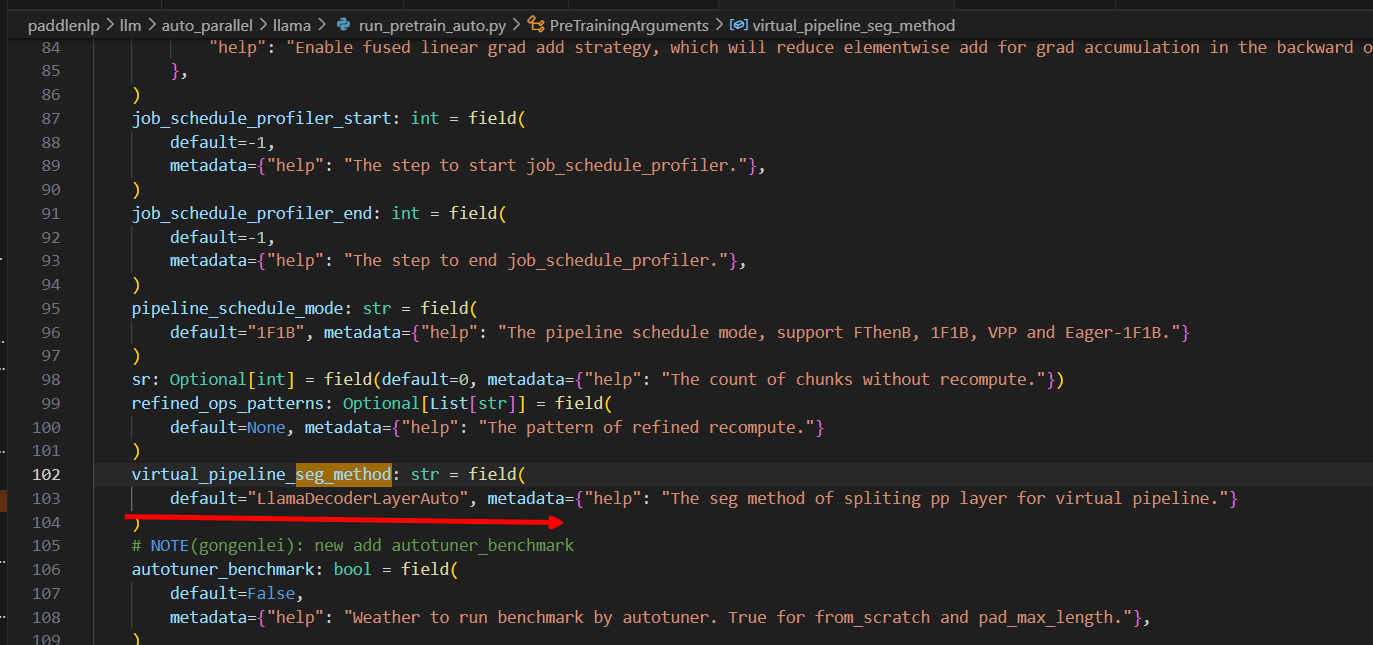
image-20241204214306982

切分方式，vpp默认为llamaDecoderLayerAuto

2.2 追溯seg_struct_names​

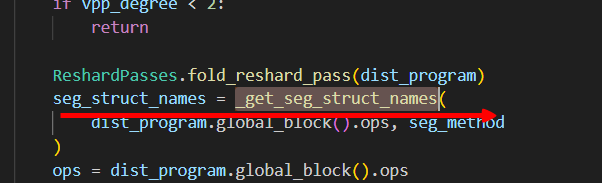
image-20241204223014677

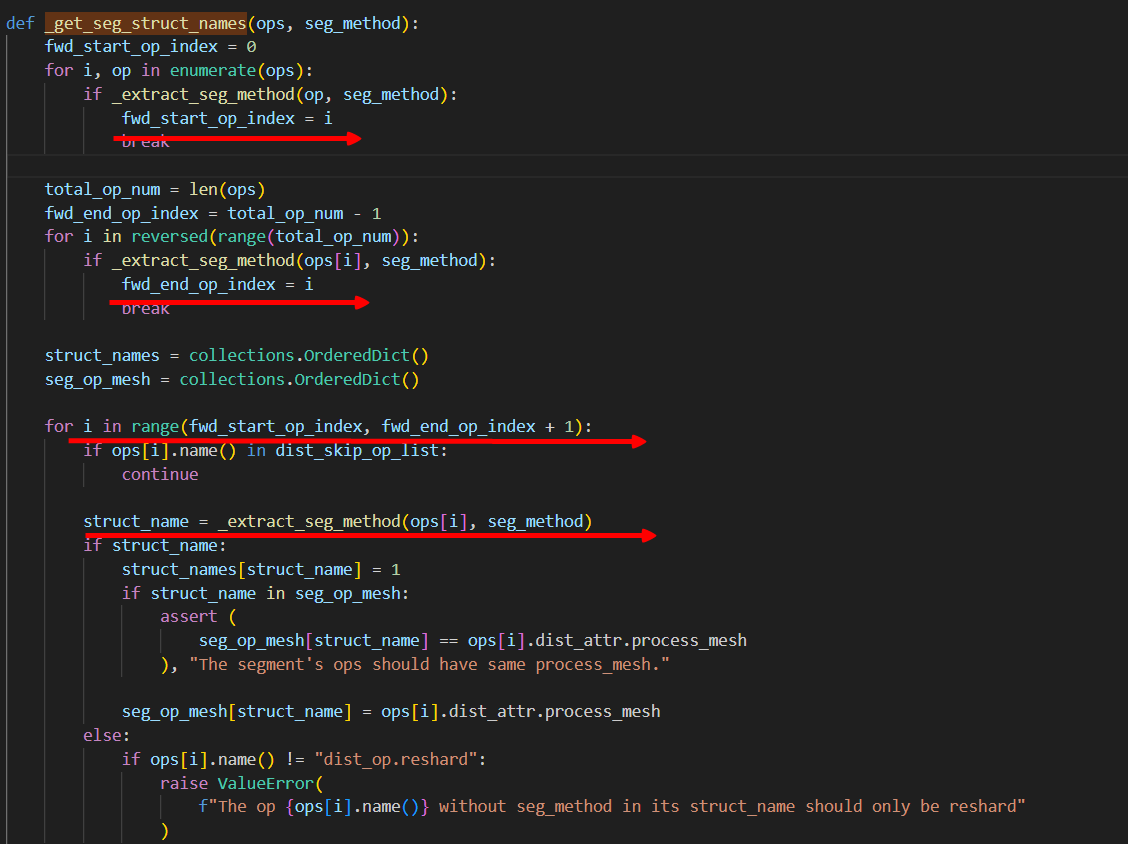
image-20241204224230809

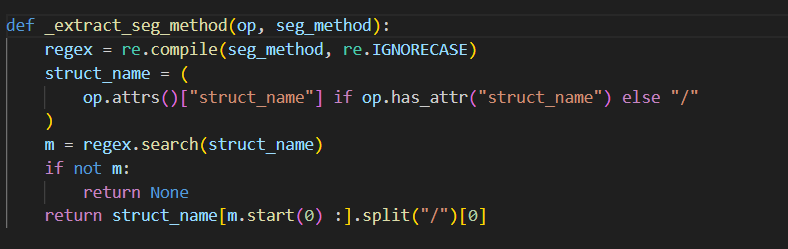
image-20241204224314354

​ 从_extract_seg_method解读发现，该函数主要是根据正则匹配表达式，匹配struct_name为seg_method（忽略大小写）的，也就是匹配算子的struct_name为llamaDecoderLayerAuto的，再看_get_seg_struct_names发现，forward算子的开始index即对所有算子从前往后找，找到第一个llamaDecoderLayerAuto，而结束的index则是从后往前找，找到第一个llamaDecoderLayerAuto，打印出来可以看到就是我们训练时设置的hidden layer的个数

image-20241204225741522

2.3 追溯vpp_reshard部分的核心代码complete_chunk_id​

step1：​

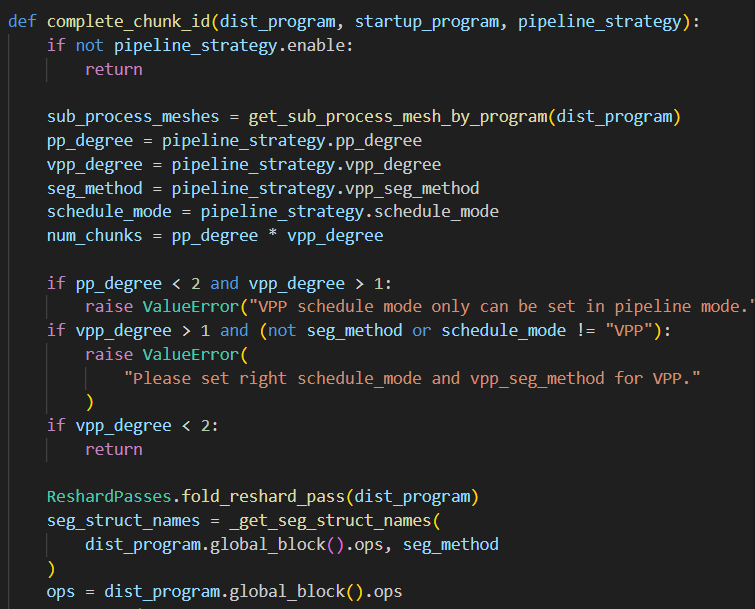
image-20241205210425837

​ 获取一些重要的元素，其中sub_process_meshes为子进程网格，即如何将计算分布到多个设备上

获取所有算子即ops

step2，3：​

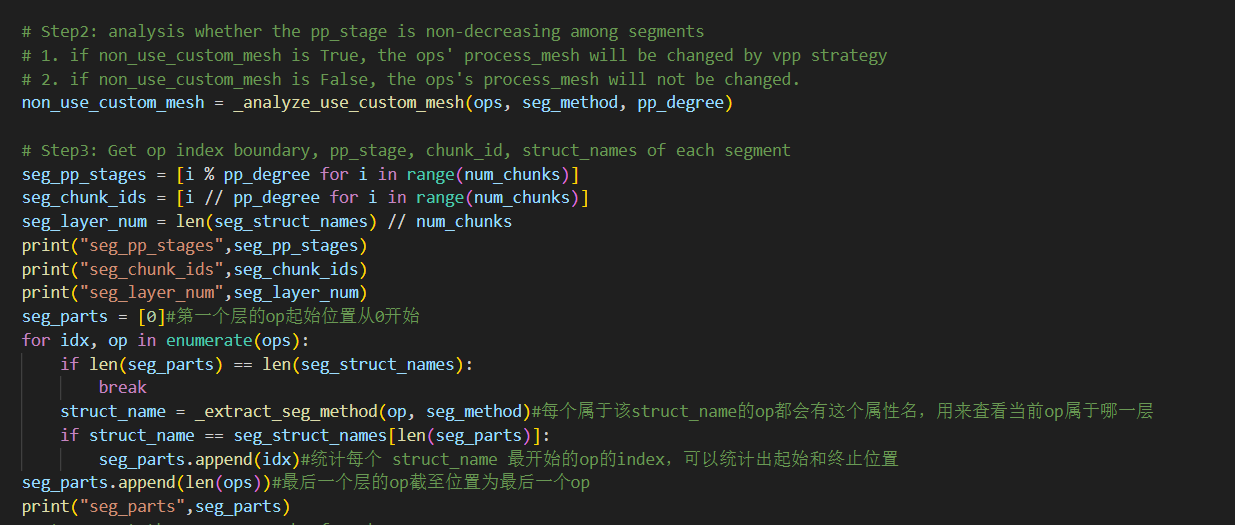
image-20241205211007895

如果用户没有指定的分配方法，则使用vpp strategy，这里按vpp的思想获取seg_pp_stages,seg_chunk_ids,seg_layer_num效果如下：

image-20241205213546698

​ 块需要按照设备交错的方式进行分布，即每个设备上的块号，相互之间是一定不会相同的，在此场景下，就是例如：0号设备，分别放0号和1号块，每个块放2层，控制逻辑还在后面的代码中，此处不详细记录。

​ 第一层的op起始index从0开始，最后一层的op终止index从最后一个op的index结束，其余的op则遍历op列表，直到找到第一个当前op的struct_name=当前层的名称，即记录每一层的最开始的那个op的index，如下：

image-20241205213844749

step4：​

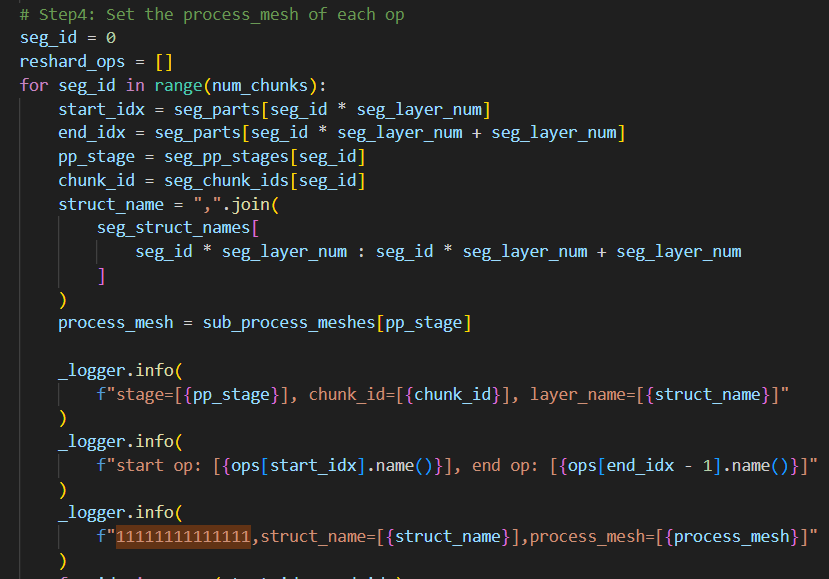
image-20241205214725649

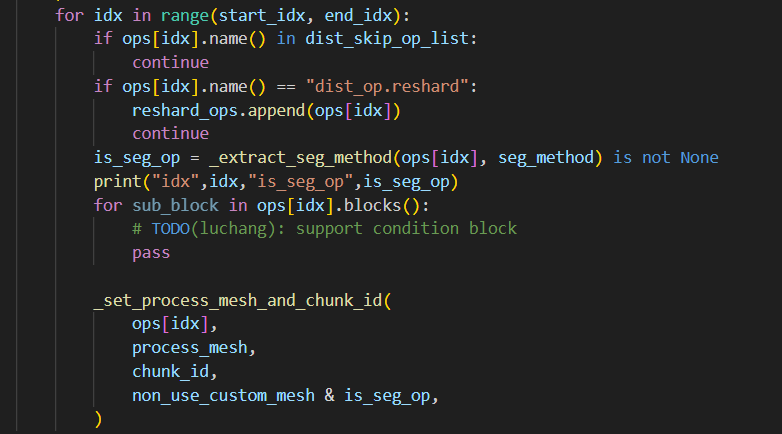
image-20241205214751624

​ 在这一步，是进行vpp reshard的主要逻辑，start_index和stop_index记录的是这一块中的所有层的起始index和终止index，因为seg_pp_stage是pp_degree对num_chunks求余得到的，所以按照num_chunks循环的时候，就遵循vpp原则，依次将chunk按照pp_stage递增的顺序放置，并且不断循环，从而达到每个"0"块放一遍所有的设备，再将每个1块放一遍所有的设备。

3.开发思路​

3.1 更改assert设置​

​ 支持 整除或者(len(seg_struct_names)+1) %num_chunks ，即支持少一层的操作，且当为少一层的操作时，此时num_chunks数不能等于len(seg_struct_names)+1，即块数不能等于层数+1，否则少一层，则有一个块是空的，当前暂不支持。

assert (
        (len(seg_struct_names) % num_chunks == 0) or ((len(seg_struct_names)+1) % num_chunks == 0 and (len(seg_struct_names)+1) // num_chunks != 1)
    ), f"The number of layers[{seg_method}] ({len(seg_struct_names)}) should be divided by part number ({num_chunks})."

3.2 少一层的设计思路​

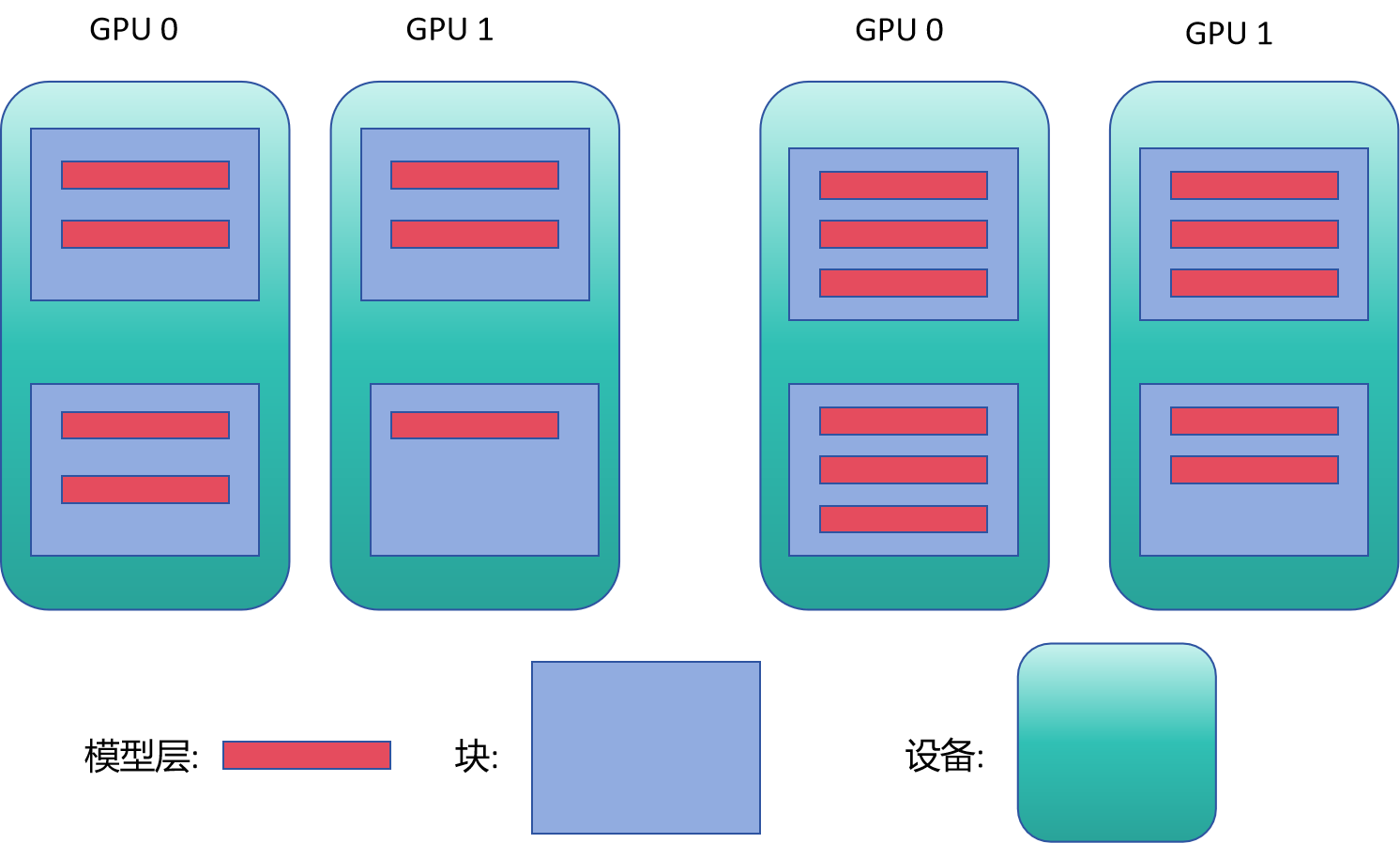
vpp去尾

  • 修改seg_layer_num的表示形式

​ 可以看到，首先左边的图，即pp少一层后，我们先分析哪些数值会变化影响结果:

    sub_process_meshes = get_sub_process_mesh_by_program(dist_program)
    pp_degree = pipeline_strategy.pp_degree
    vpp_degree = pipeline_strategy.vpp_degree
    seg_method = pipeline_strategy.vpp_seg_method
    schedule_mode = pipeline_strategy.schedule_mode
    num_chunks = pp_degree * vpp_degree
    seg_pp_stages = [i % pp_degree for i in range(num_chunks)]
    seg_chunk_ids = [i // pp_degree for i in range(num_chunks)]
    seg_layer_num = len(seg_struct_names) // num_chunks

​ 观察重要参数seg_pp_stages、seg_chunk_ids、seg_layer_num,其中seg_pp_stages为[0,1,0,1]不变，seg_chunk_ids为[0,0,1,1]不变，seg_layer_num发生了变化，即从2变成了1，而根据我们的图示可以看到，我们此时希望的仍然是seg_layer_num为2，只有最后一个chunk的seg_layer_num为1，因此，我们将此处seg_layer_num给换掉，让其和块对应起来，即如下代码：

seg_layer_num=[0]*num_chunks#记录每个块里面的层数
    for j in range(0,len(seg_struct_names)):#把层数分别分给每个块，保证每个块至少先被分一层，按此逻辑可以支持少多层，只要保证每个块至少一层
        i=j%num_chunks
        seg_layer_num[i]=seg_layer_num[i]+1

把后续的所有seg_layer_num用seg_layer_num[seg_id]代替即可

​ 带入右边的情况验证，同样支持，因此该操作可以在任意模型隐藏层层数hidden_layer整除vpp_degree时，去掉一层隐藏层，从而使得前面每一个chunk都分到相同的层数，只有最后一个chunk少一层，此时能保证chunk数不变，这样做的目的，一方面是为了每个chunk的时间保持均匀的同时，去掉一层hidden_layer。

  • 修改每个块包含的算子的起始index和终止index的表示形式

​ 首先，因为seg_layer_num变成了列表，因此需要将表示形式修改，同时因为原来的代码如下所示：

        start_idx = seg_parts[seg_id*seg_layer_num]
        end_idx = seg_parts[seg_id*seg_layer_num + seg_layer_num]

​ 可以看到，当seg_layer_num相同时，代码没有问题，但是当最后一层少了一层时，此时最后一层的start_idx和end_idx计算是有问题的，为了后续工作进行，我们在这里不做特殊处理，而做统一表示，即如下代码：

    previous_seg_parts_end_idx=0#记录上一个终止点对应的seg_parts的index
    for seg_id in range(num_chunks):
        start_idx = seg_parts[previous_seg_parts_end_idx]#seg_layer_num需要改成对应块的层数，即用seg_layer_num[seg_id]代替
        end_idx = seg_parts[previous_seg_parts_end_idx + seg_layer_num[seg_id]]

​ 我们引入一个previous_seg_parts_end_idx用来记录上一个块的终止的算子对应的seg_parts的index，起始也就是对应的层标号

  • 修改struct_name

​ 同时我们将struct_name也做如下修改，同样是保证hidden_layer不整除vpp_degree时，struct_name能得到正确的值。

 struct_name = ",".join(
            seg_struct_names[
                previous_seg_parts_end_idx : previous_seg_parts_end_idx + seg_layer_num[seg_id]
            ]
        )
        previous_seg_parts_end_idx=previous_seg_parts_end_idx + seg_layer_num[seg_id]#更新终止点的index
  • 更新previous_seg_parts_end_idx

​ 最后更新previous_seg_parts_end_idx，即等于当前的更新终止点在seg_parts中的index。