旋转位置编码(RoPE/Rotary Position Embedding)
1.基本概念:
首先定义一个长度为 N 的输入序列为:
其中 wi 表示输入序列中第 i 个 token,而输入序列 SN 对应的 embedding 表示为:
其中 xi 表示第 i 个 token wi 对应的 d 维词嵌入向量。接着在做 self-attention 之前,会用词嵌入向量计算 q, k, v 向量同时加入位置信息,函数公式表达如下:
其中 qm 表示第 m 个 token 对应的词向量 xm 集成位置信息 m 之后的 query 向量。而 kn 和 vn 则表示第 n 个 token 对应的词向量 xn 集成位置信息 n 之后的 key 和 value 向量。而基于 transformer 的位置编码方法都是着重于构造一个合适的 f{q,k,v} 函数形式。而计算第 m 个词嵌入向量 xm 对应的 self-attention 输出结果,就是 qm 和其他 kn 都计算一个 attention score ,然后再将 attention score 乘以对应的 vn 再求和得到输出向量 om:
这里可以根据这个图来理解:
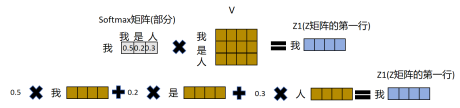
最后计算出的这个Z矩阵的这一行,就是这里的Om,而得到这一行结果的过程,就是对于第m个token用其分别对第n个token的attention乘以对应的V,得到最终的结果,其实这就是一个加权计算的操作,对第m个token来说,会将与其attention较强的token的特征放大,而较弱的特征降低。
2.绝对位置编码(RoPE)的提出理由
对于位置编码,常规的做法是在计算 query, key 和 value 向量之前,会计算一个位置编码向量 pi 加到词嵌入 xi 上,位置编码向量 pi 同样也是 d 维向量,然后再乘以对应的变换矩阵 W{q,k,v}:
而经典的位置编码向量 pi 的计算方式是:
其中 p_{i,2t} 表示位置 d 维度向量 pi 中的第 2t 位置分量也就是偶数索引位置的计算公式,而 p_{i,2t+1} 就对应第 2t+1 位置分量也就是奇数索引位置的计算公式。代码如下:
# position对应token序列中第i个token的位置
# hidden_dim表示词嵌入维度大小,即Vocab的列大小
# seq_len表示 token的序列长度
def get_position_angle_vec(position)
return[position/np.power(10000,2*(hid_j//2)/hidden_dim) for hid_j in range(hidden_dim)]
# position_angle_vecs.shape = [seq_len, hidden_dim]
position_angle_vec = np.array([get_position_angle_vec(pos_i) for pos_i in range(seq_len)])
#分别计算奇偶索引对应的sin 和 cos值
position_angle_vecs[:,0::2]=np.sin(position_angle_vec(:,[0::2]) #在hidden_dim上,从0开始走到最后,每次走两步,即偶数项
position_angle_vecs[:,1::2]=np.sin(position_angle_vec(:,[1::2]) #在hidden_dim上,从1开始走到最后,每次走两步,即奇数项
# positional_embeddings.shape = [1, seq_len, hidden_dim]
positional_embeddings = torch.FloatTensor(position_angle_vecs).unsqueeze(0)#通常第一个维度为batch_size
为什么要hid_j//2
这里注意t并不表示hidden_dim的每一个hid_j的第j个位置,而是为hid_j//2,原因是为了让每一对相邻的sin,cos组成一个同频率的正余弦,从而在计算self-attention时,可以隐式计算相对位置,即用三角函数恒等式:sin(a)sin(b)+cos(a)cos(b)=cos(a−b)。PE公式里除去位置参数,剩下的分数其实就表示当前sin和cos的频率。
在计算时,对于位置i和位置j有如下公式:
而展开后,最后一项其实就暗含了相对位移的信息:
因为对于位置i,j分别有:
那么相乘展开后会存在,比如第k组维度如下:
则,两者做点积有:
而利用恒等式有:
所以:
此时即可以得到第k组维度下的相对位置的值。
注意,cos是一个周期函数,所以对于位置π→2π 与 π→6π的相对距离算出来一样,即单频率不能区分大距离,远距离信息会被冲输掉,为了更好地显示表示相对位置信息,并且在较长的文本下也有比较好的效果,并且原来的x+p本质上还是绝对位置信息,而相乘之后只有一项包含位置信息,中间第2,3项是位置信息与文本信息的交互属于噪声项,让模型在这样的场景下去学习到位置信息还是比较困难得,因此提出了RoPE。
3.RoPE的推导
RoPE证明了用当前的公式,即计算出的q,v分别两两一组旋转,并做内积,可以转换成一个只依赖于input_embedding和相对位置的等效公式,根据理论,我们知道它正在有效地计算 "相对位置" 的得分。可以更加有效地学习到相对位置的信息。
论文中提出为了能利用上 token 之间的相对位置信息,假定 query 向量 qm 和 key 向量 kn 之间的内积操作可以被一个函数 g 表示,该函数 g 的输入是词嵌入向量 xm , xn 和它们之间的相对位置 m - n:
接下来的目标就是找到一个等价的位置编码方式,从而使得上述关系成立。这样最终q_m和k_n的内积操作就和三个变量相关,第m个token的embeddng信息,第n个token的embeddng信息,以及m和n的相对位置信息,从而将m与n的相对位置显示引入。
假定现在词嵌入向量的维度是两维,即d=2,则可以利用2维度平面上的向量的几何性质,论文提出了一个满足上述关系的f和g的形式如下:
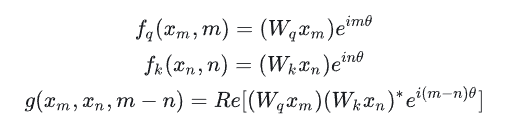
公式f和g中都有一个指数函数,这个其实就是欧拉公式,x表示任意实数,而e则是自然对数的底数,i是复数中的虚数单位:
所以上面的指数函数可以表示为实部是cosx,虚部是sinx的一个复数,所以可以写成:
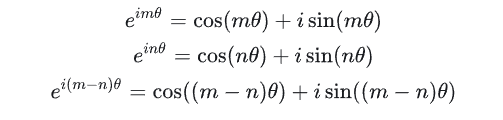
再来看看公式f:
其中 Wq 是个二维矩阵,xm 是个二维向量,相乘的结果也是一个二维向量,这里用 qm 表示:
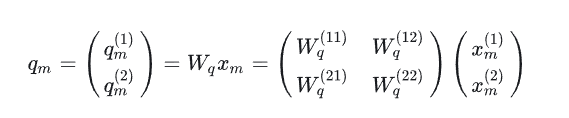
然后首先将 qm 表示成复数形式:
则可以表示为:
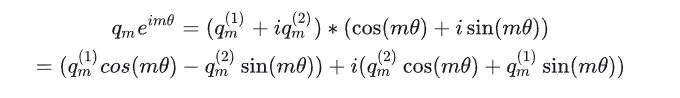
将结果重新表达成实数向量形式就是:
此时可以看到,其实就是将query向量乘以了一个旋转矩阵,逆时针旋转:
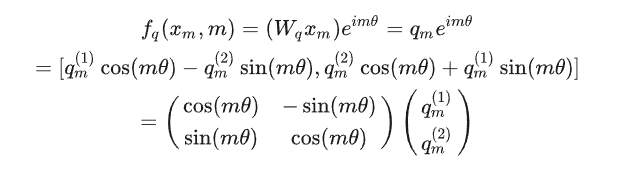
同理key向量k_n也能这么做:
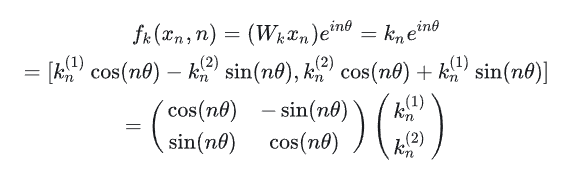
最后还有一个函数g:
其中Re[X]表示一个复数x的实数部分,而则表示复数的共轭。共轭复数定义如下:
所以可以得到:
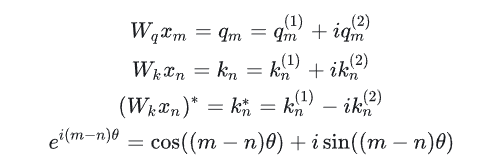
继续推导可得:
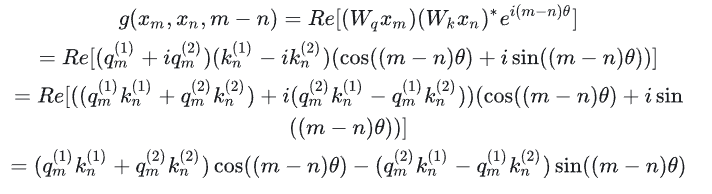
接着我们需要证明等式成立,则来计算一下f_q和f_k的内积:

再利用三角函数化简:

这就证明上述关系是成立的,位置 m 的 query 和位置 n 的 key 的内积就是函数 g。
把上面的式子用矩阵向量乘的形式来表达就是:
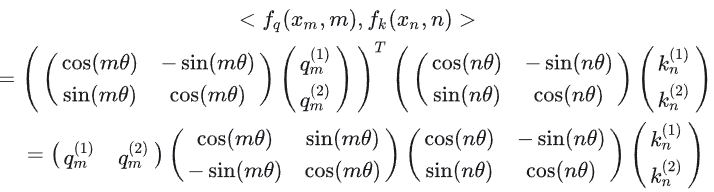
继续推导中间两项的计算:
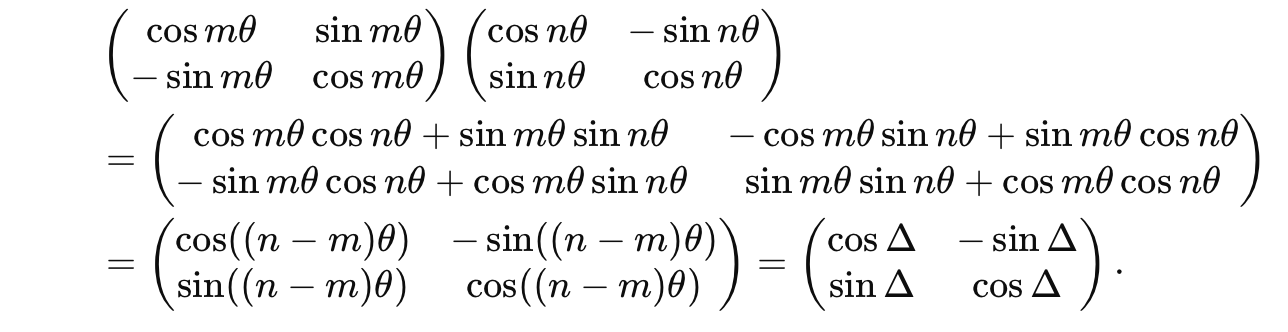
则上式可以化简为:
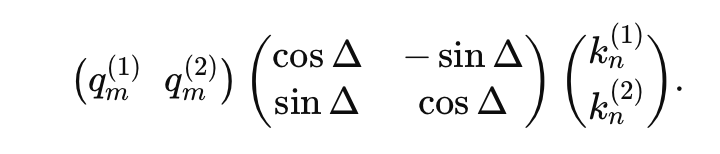
即在做attention之前,将Key矩阵做一个旋转,旋转角度为。
上面的讲解是假定的词嵌入维度是2维向量,而对于d >= 2` 的通用情况,则是将词嵌入向量元素按照两两一组分组,每组应用同样的旋转操作且每组的旋转角度计算方式如下:
为什么这里对于一个token来说,要有这么多不同的频率?同时这个公式有什么意思?
主要原因是通过在嵌入向量中包含多种频率,RoPE 使得 和 的不同维度能够同时关注和编码不同尺度的相对距离信息,就像傅里叶分析一样,用不同频率的波叠加来表示复杂信号。 高频率可以关注更短距离的信息,而低频率可以关注更长距离的信息。
这里使用和Sinusoidal位置编码一样的公式,可以带来远程衰减性,首先直接看上面的最后的推导公式,可以发现,对于两个位置m和n的token,其实就是对k做一个的旋转,再计算内积,如果不加旋转,即位置信息,此时只要两个向量足够相似(文本相似度),这个attention分数就会很高,而加上旋转后,如果n和m距离较远,则该旋转角度很较大,那么也会相对的使得q,k的相似度较小,最终的attention计算是通过多个维度,即两两不同组频率的贡献累加在一起获得的,而这里就体现了****在远程衰减性质中的重要作用,当距离较远时,超低频的嵌入分量,周期极长,在很远的距离内依然保持正值(),提供稳定的长程信号,即它此时还未完全循环一轮(指周期性函数的一个周期)。
上面的内容证明了,将q的词嵌入向量和k的词嵌入向量两两一组,分别进行旋转,旋转的角度,这里m表示绝对位置,再做self_attention的计算可以有效地表示input的文本信息和相对位置的信息。
因此RoPE的self-attention具体操作如下,输入的X先做embedding,得到词嵌入向量,紧接着在算self_attention之前,对query和key向量,每个token位置的向量元素,相邻之间两两一组做旋转变换,两两一组是因为上述分析是在词嵌入向量为2维的假设下做的推导,然后再计算query和key的内积,得到self-attention,此时的self-attention即能表现input的文本信息,也能表现相对位置信息。
如下图所示清晰展现了整个过程:
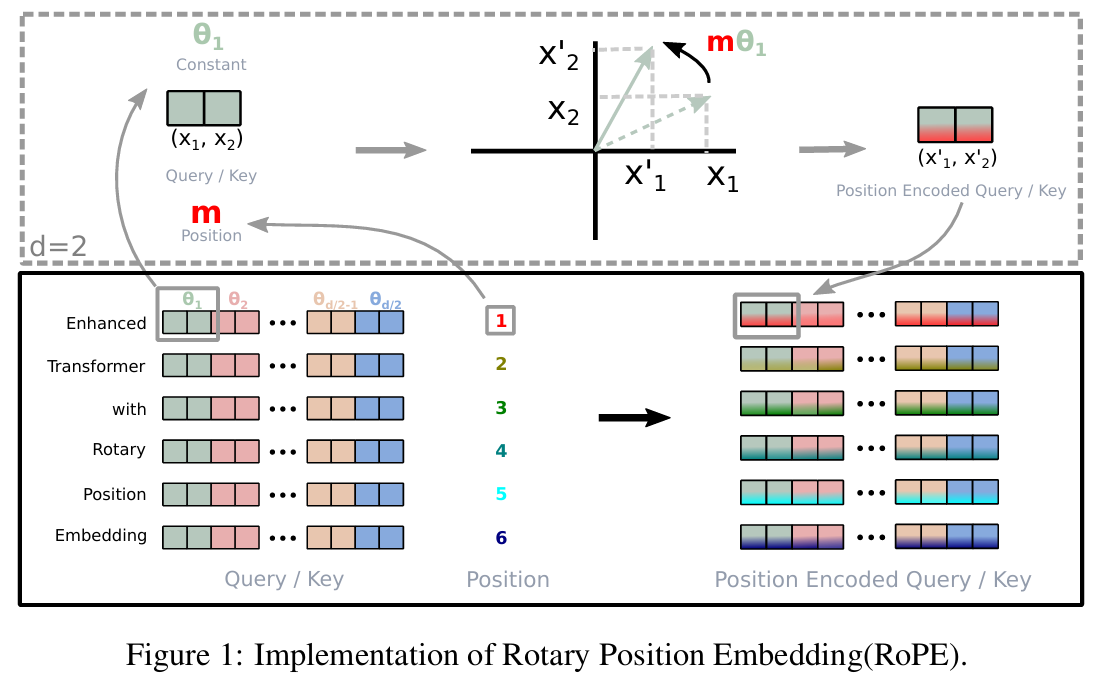
通�过简单的旋转,将位置信息嵌入到了词嵌入向量中。
LLaMA官方代码如下:
def precompute_freqs_cis(head_dim:int, seq_len: int, thetaL float = 10000.0)
# 计算词向量元素两两分组之后,每组元素对应的旋转角度,注意这里取[0:head_dim/2]是因为当head_dim维度为基数时,最后一个数不做旋转。
freqs = 1.0 / (theta ** (torch.arange(0,head_dim,2)[:(head_dim//2)].float())/head_dim)
#生成 token 序列索引 t=[0,1,2,...,seq_len-1]这个表示的是token的绝对位置,从0开始
t = torch.arange(seq_len,device=freqs.device)
#外积,一般只列向量n*1与行向量1*n相乘得到n*n的矩阵
#让每一个绝对位置m和θ相乘,得到每个token每一组嵌入向量的旋转角度,mθ,则freqs形状变为:freqs.shape= [seq_len,head_dim//2]
freqs = torch.outer(t,freqs).float()
#freqs_cis.shape= [seq_len,head_dim//2],且每个都是cos + isin的形式
freqs_cis = torch.polar(torch.ones_like(freqs),freqs)
return freqs_cis
def apply_rotary_emb(
xq:torch.Tensor,
xk:torch.Tensor,
freqs_cis: torch.Tensor,
) -> Tuple[torch.Tensor,torch.Tensor]
# xq.shape = [batch_size,seq_len,head_dim]
# xq_.shape = [batch_size,seq_len,head_dim//2,2]
# 这里的操作是将原来的tensor,reshape成([除去最后一维的形状],-1(自动推导形状),2),即增加一个维度,并将最后一个维度拆分成dim//2,2
# 这个操作把两两相邻的元素组合成了一组,dim//2中表示每一组的组号,也对应上面t的最后一维。
xq_ = xq.float().reshape(*xq.shape[:-1],-1,2)
xk_ = xk.float().reshape(*xk.shape[:-1],-1,2)
# 转到复数域,最后一个维度大小只能是2,将tensor的最后一维两两配对,变成实部和虚部,同时减少一个维度,变成[batch_size,seq_len,head_dim//2]
xq_ = torch.view_as_complex(xq_)
xk_ = torch.view_as_complex(xk_)
# 应用旋转操作,freqs_cis与batch无关,所以实际计算时会广播,即复制batch_size份freqs_cis
# 每组元素相乘,即转为复数域的向量域对应的cos + isin的旋转操作相乘,得到旋转后的向量
xq_Ro = xq_ * freqs_cis
xk_Ro = xk_ * freqs_cis
# 然后将结果转回实数域,[batch_size,seq_len,head_dim//2,2],从第二个维度以后全部展平
# xq_out.shape=[batch_size,seq_len,head_dim]
xq_out = torch.view_as_real(xq_Ro).flatten(2)
xk_out = torch.view_as_real(xk_Ro).flatten(2)
return xq_out.type_as(xq),xk_out.type_as(xk)
class Attention(nn.Module):
def _init_(self,args:ModelArgs):
super().__init__()
self.wq=Linear(hidden_dim,head_dim)
self.wk=Linear(hidden_dim,head_dim)
slef.wv=Linear(hidden_dim,head_dim)
#max_seq_len*2表示预留的长度
self.freqs_cis = precompute_freqs_cis(head_dim,max_seq_len*2)
def forward(self,x:torch.Tensor)
bitch_size,seq_len,hidden_dim =x.shape
head_dim = hidden_dim/head_nums
xq,xk,xv = self.wq(x),self.wk(x),self.wv(x)
#应用旋转位置编码
xq,xk = apply_rotary_emb(xq,xk,self.freqs_cis)
#计算attention
scores = torch.matmul(xq,xk.transpose(1,2))/math.sqrt(head_dim)
scores = F.softmax(scores.float(),dim=-1)
output = torch.matmul(scores,xv)
一些代码解释:
1.算出来的freqs.shape= [seq_len,dim//2]的格式如下:
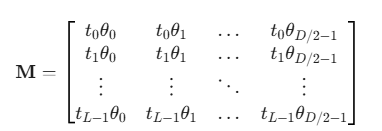
这里是得到了每个q,k的head_dim维度的两两一组的元素需要旋转的角度。
2.freqs_cis的含义
由于我们计算出了旋转角度,此时需要做两两元素的旋转如下:
则我们需要对每一对元素都要构建旋转矩阵,然后如果转换到复数域下:
所以这一步的目的是将其转化到复数域,即矩阵每个元素都变成cos+isin的形式,后续与每组元素相乘即可得到结果,无需构建大量的旋转矩阵。
torch.polar(r,θ)的作用是,把极坐标转换成复数域,这里因为的系数就是1,因此r就传入一个等量大小的one矩阵。
freqs_cis的形式如下:
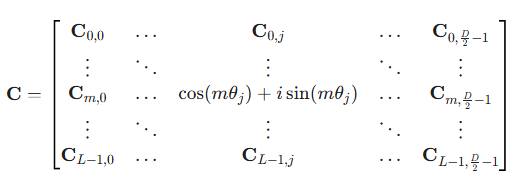
同时v'乘以C可以表示为:
所以旋转后的新坐标:
所以:
因此在工程代码中通常使用的是 ,是Q的一个大小的分量,rotae_half表示逆时针旋转90°。
4.RoPE特点总结
1.旋转编码 RoPE 可以有效地保持位置信息的相对关系,即相邻位置的编码之间有一定的相似性,而远离位置的编码之间有一定的差异性。
2.旋转编码 RoPE 可以通过旋转矩阵来实现位置编码的外推,即可以通过旋转矩阵来生成超过预训练长度的位置编码。并且多频混合保证了其不会重复,因为比如组此时转完了一圈,但是这些组还在旋转,所以只要n个组合不完全一致,位置编码就是唯一的。
3.旋转编码 RoPE 可以与线性注意力机制兼容,即不需要额外的计算或参数来实现相对位置编码。
5.ALiBi位置编码
不添加position embeding,而是添加一个静态的不学习的bias代替positon embeding:
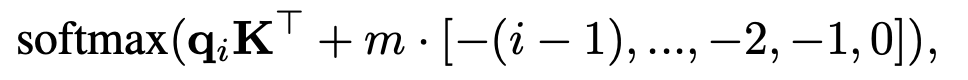
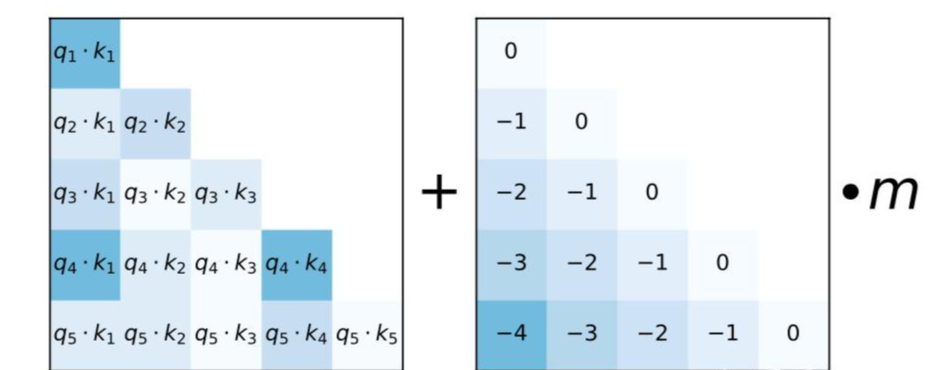
根据相对距离,这个bias逐渐增加,对于8个attention head 的例子,每个头的权重m不同,范围为,对于16个attention head,则每个头的权重m为。
ALiBi主要强调外推性,并且主要是展现了可以在较短序列训练,而在超长序列的情景推理,并且模型预测的困惑度相对其��它方法相对较低。但是该方法没有从其它指标去验证模型的外推性,并且生成式模型首先需要确保在max_seq_len内保证生成的效果,然后再去提高外推性,而ALiBi仅仅关注于模型外推性。