Attention_Head（MHA、MQA、GQA、MLA）

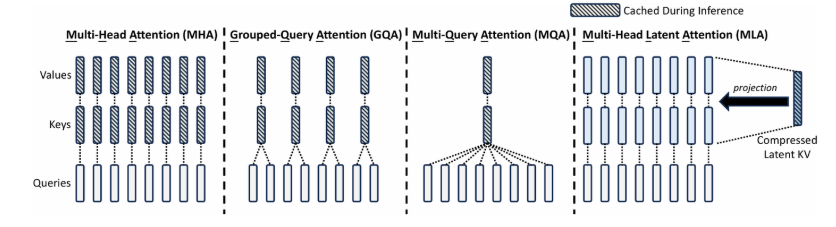
多头注意力机制包含MHA、GQA、MQA、MLA以上四种。

1.MHA

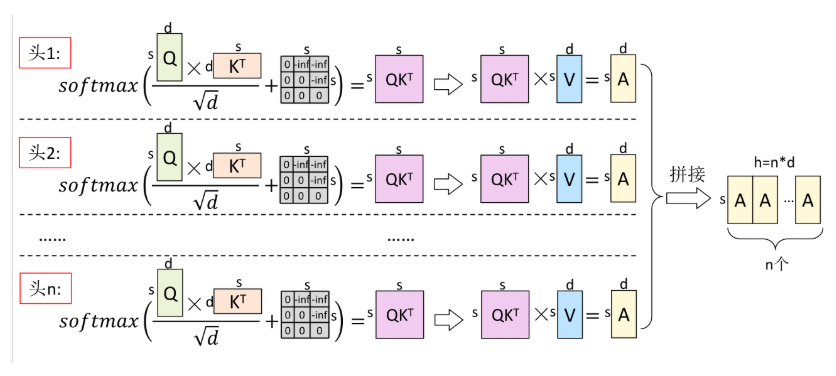
​ 最早提出的是MHA，即Multi-Head Attention，每一个Query头对应一组K-V对，在推理过程中，计算Attention时，每次都要计算历史的QKV矩阵，速度较慢，为了加速，提出了KV Cache的策略，但是KV Cache会随着推理的token增加，逐渐增大，占用显存越来越大，因此就提出了其它的方法。

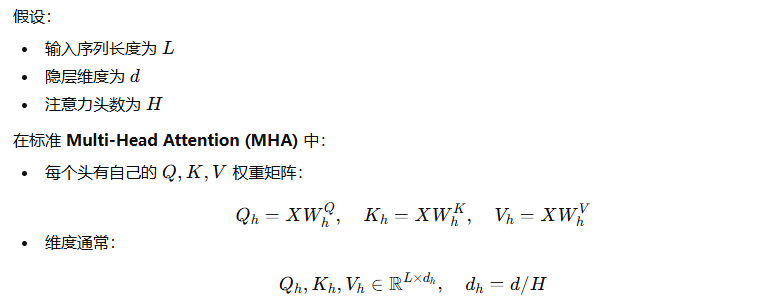
​ 注意Q,K,V的维度此时是 $d_h$，而后续的MQA、GQA并不会改变Q,K,V的维度，只是通过共享操作来减少计算量。

2.MQA

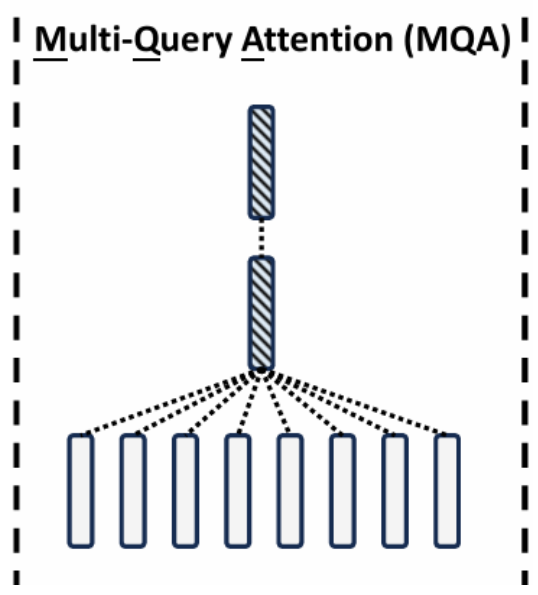
​ 在此基础上，既然KV cache如此占显存，那么久减少KV对的使用，即使用一个共享版本，Multi-Query Attention。可以看到，此时每个head的Query都共享K和V矩阵，则KV cache的显存占用直接降低到了1/n，然后这样做容易导致模型的性能下降，严重的还会导致模型的稳定性，因此又选出了折中的方法。

​ 常用模型包括PALM、StarCoder、Gemini等。

3.GQA

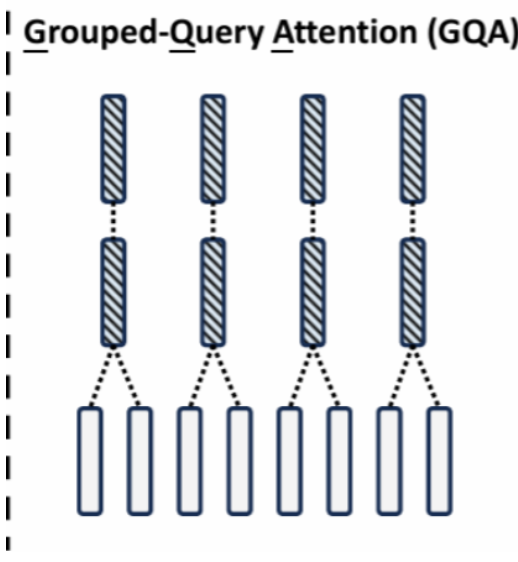
​ GQA是在使用group_nums对Query进行分组，g=1就是MQA，g=n就是MHA。常用模型包括LLAMA2-70B，LLAMA3全系列，DeepSeek-V1，Qwen3-MOE系列，ChatGLM3等。

​ 注意，这里是一组K,V对，对应多个Q

4.MLA

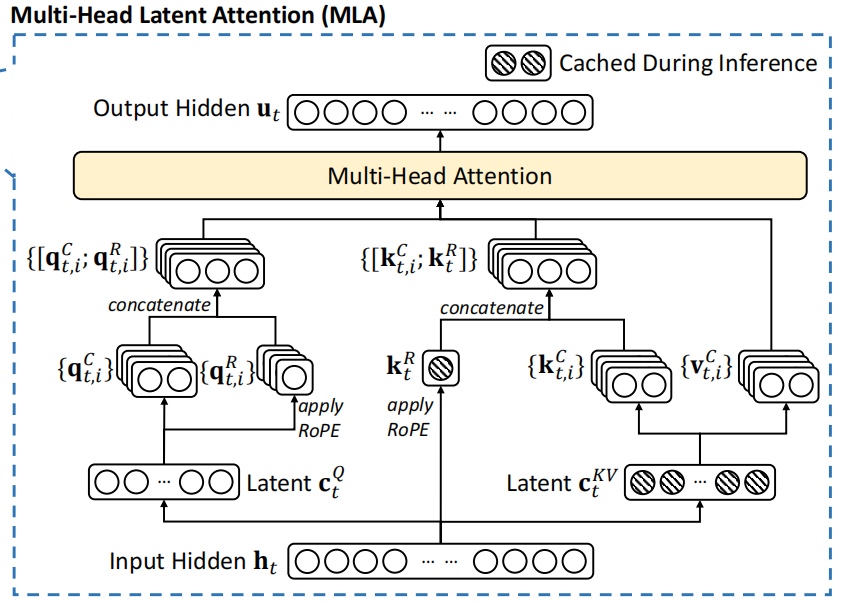
​ 如图是MLA的一个总览图，先在此做一个总结：

​ 1.MLA整个过程包含MHA和MQA，MQA体现在对于position embedding的处理，所有的Q共用同一个RoPE的K。因此图中的 $k_t^{R}$ 会被复制或者说广播和其它 $k_t^{C}$ 进行拼接，后续都是一个Q对应一组KV，也就是MHA。

​ 2.MLA整个过程缓存的是 $c_t^{KV}$ 和 $k_t^{R}$：

​ $c_t^{KV}$ 其实是对输入 $x$ 或者上一层输入的隐藏状态 $h_t$ 做一个降维的操作，即乘以一个降维矩阵，后续要获取 $k_t^{C}$，$V_t^{C}$ 仅需要通过对这个降维后的矩阵 $c_t^{KV}$ 做一个升维的操作即可，而这个过程其实是对原来的 $W_k$，$W_v$ 做了降秩的操作。即原来计算量是 $2*d*d$，现在是 $3*d*d_c$。

​ $k_t^{R}$ 则是对输入 $x$ 或者上一层输入的隐藏状态 $h_t$ 做一个降维的操作，并接着做RoPE，文中降低到了 $d_h^{R}=d_h/2=64$，作者认为仅用这么高的维度即可表现位置信息。

​ 3.MLA仅在推理的Decoding阶段使用

​ 4.从上述结论也可以看出，所有的input_embedding和position_embedding是分为两份矩阵表示，并且每个头分别拼接这两份向量，组成最终的Q，K也同样，组合后，再做attention。

​ 5.MLA的操作可以总结为：

​ 1.矩阵吸收(计算图优化)——利用矩阵乘法的链路最优解，将self_attention以及输出矩阵O的整个计算结合，找出最优计算次数最少的矩阵乘法方式。

​ 2.低秩投影，引入降秩的概念，用两个d*r的矩阵将原来的d*d的矩阵给降秩，从而大大降低计算量。

​ **3.如果仅仅引入计算图优化，相比于KV Cache，显存的确降低了，但是也增加了一些计算量，即时间换空间，所以引入了降秩的概念，进一步降低显存，并且计算量的增加也会减少很多。1，2的引入，使得MLA可以保存比KV Cache占用显存更小的 $c_t^{KV}$ 和 $k_t^{R}$，从而解决KV Cache的显存瓶颈问题 **

1.MLA概念分析

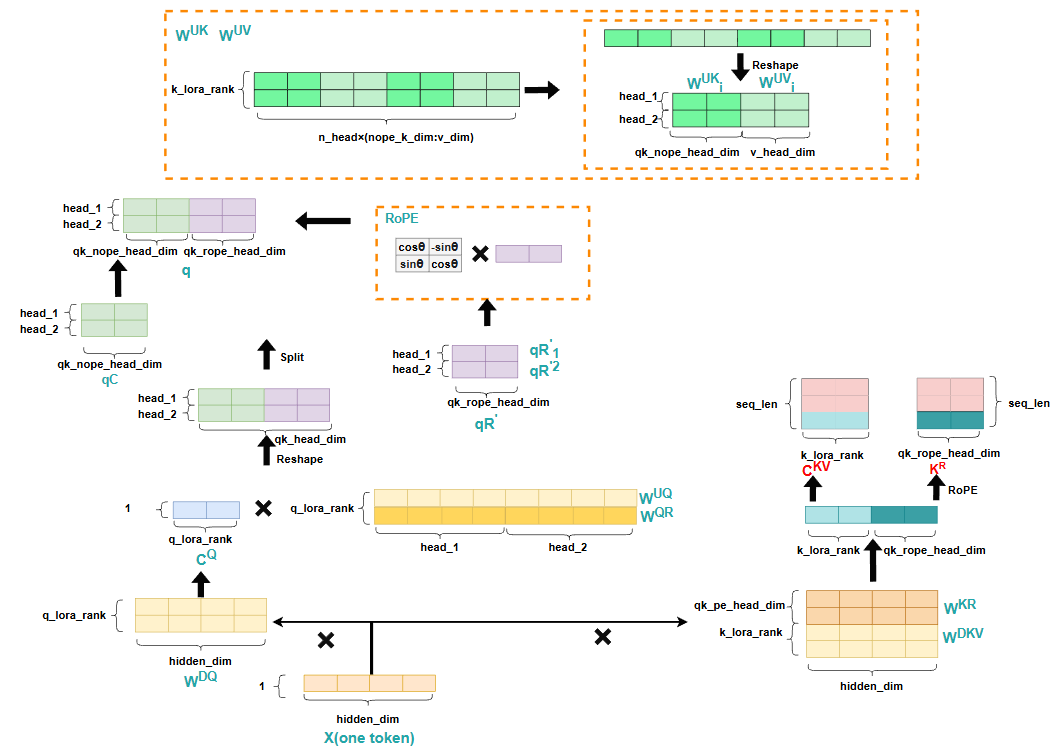
​ 元素推导

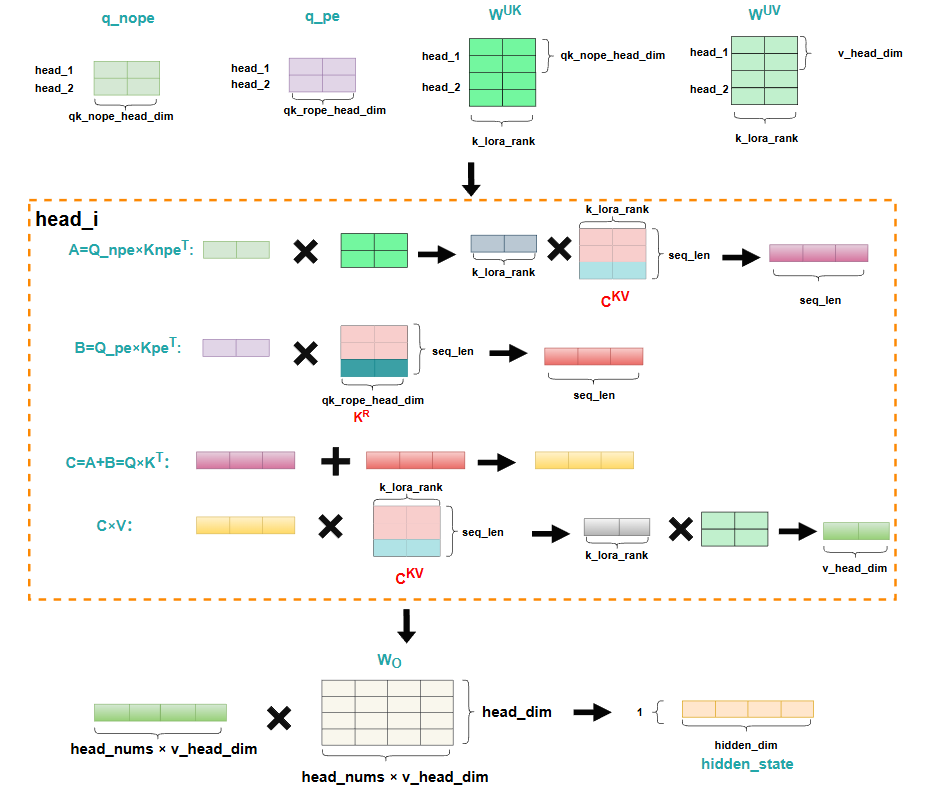
​ 元素计算流程

​ 整个Decoding计算流程如下：

​ 在推理每一个token时，仍然只需要输入计算出的结果的最后一个隐藏层状态，并且对于Q来说，首先与 $W^{DQ}$ 相乘，再乘一个相同大小的矩阵 $W^{UP}$，这个操作实际就是降秩，减少计算量，最后得到的Q的大小仍然没变，与传统方法不同的是，这里会将context与position信息解耦，即不再在计算出的 $q$ 矩阵上去做RoPE，而是利用同样的降秩操作，最后得到一个hidden_size较小的矩阵，并按照head_nums做分割，分配每个head，然后分别对每个小矩阵做RoPE，最终每个attention头都得到了带有position信息的矩阵，然后将context矩阵 $q^{C}$ 和position矩阵 $q^{R}$ 进行拼接，从而得到 $q$。

​ 对于k和v，同样会用降秩的思想，即分别乘以一个 $W^{DKV}$ 和 $W^{UK}$ 从而实现减少计算量，而对于K来说，同样会将context与position信息解耦，但是注意这里计算 $K^{R}$ 时，即K的position信息的矩阵，其维度是 $q^{R}$ 的维度 $d_h^{R}/q_{nums}$，因为这里的 $K^{R}$ 其实是所有attention头共享的，即MQA的思想。最后计算出 $K^{C}$,$V^{C}$，同样将context矩阵 $K^{C}$ 和position矩阵 $K^{R}$ 进行拼接，从而得到 $k$。

​ 通过这样的计算过程可以看到，此时我们只需要保存 $C^{KV}$ 和 $K^{R}$ 这两部分数据，即可在每次forward过程迅速恢复K,V的信息，并且相比于直接保存K,V，整个显存也大大降低了，原来是 $2*seq_len*head_nums*head\_dim$，而现在变成了 $(hidden\_dim*d_k^{R}+d_{KV}*seq_len)$，其中 $d_{KV}$ 与 $d_k^{R}$ 都非常小。

​ 但仅仅如此，会发现我们仍然要根据 $C^{KV}$ 把K,V这两个矩阵给重新计算出来，仍然存在较大的计算量，那如何优化这一点呢，这就是上面提到的，灰色箭头，实际计算并没有按照灰色箭头的方向，逐渐把K,V矩阵算出来，而是把 $W^{UK}$ 分别吸收进了 $W^{UQ}$ 矩阵与 $W^{O}$ 矩阵。具体吸收方法见MLA的公式推导分析。

2.MLA公式推导分析

2.1 X-Cache

​ 首先我们来单纯分析一下，优化attention的整个计算图，从而来降低计算量，对于单个头分析。

​ 对于非KV Cache来说，我们先分别计算一个token的q，k，v，即 $1×d$ 大小的矩阵和 $d×d_h$ 大小的矩阵相乘，得到q,k,v的大小为 $1×d_h$ 然后利用self_attention公式计算出score，最后和Wo相乘，计算公式如下（注意这里是以单个头的视角分析，实际操作是每个attention的结果拼接成一个大矩阵，得到N×d大小的矩阵，然后和大小为d×d大小的矩阵Wo相乘，而此时乘的Wo是大Wo的单个头的切片，因为根据矩阵乘法性质，$(x_1,x_2,...,x_n)\times(y_1,y_2,...,y_n)^T$ 等价于 $x_1y_1+x_2y_2+...+x_ny_n$）：

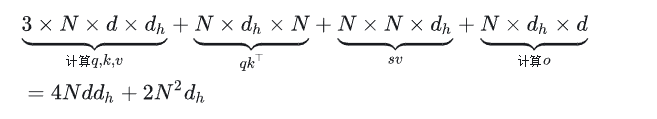
​ 对于KV Cache来说，我们先分别计算一个token的q，k，v，即 $1×d$ 大小的矩阵和 $d×d_h$ 大小的矩阵相乘，得到q,k,v的大小为 $1×d_h$ 然后k，v拼接到之前的cache中，得到一个 $N×d_h$ 大小的矩阵K和V，N表示seq_len，然后利用attention公式，计算得到score矩阵，大小为 $N×d_h$，最后和大小为 $d_h×d$ 输出矩阵 $W_o$ 相乘，得到最终的输出：

​ 而对于X Cache来说，我们只用缓存每次的X，但是会发现，X并没有减少计算量，K,V仍然需要计算，不过这时候我们改变与一下计算顺序，即先算 $(x^T W_q W_k^T)$，再乘以X，紧接着乘以 $X^T$，再算 $W_v W_o$ 的结果，最后左右两边结果相乘。所以矩阵计算顺序为，先算大小为 $1×d$ 的矩阵x和大小为 $d×d_h$ 的矩阵 $W_q$ 的乘积，得到大小为 $1×d_h$ 的矩阵，紧接着与大小为 $d_h×d$ 的 $W_k^T$，得到矩阵 $1×d$，再和大小为 $d×N$ 的矩阵X相乘，得到大小为 $1×N$ 的矩阵，此时再和大小为 $N×d$ 的矩阵 $X^T$ 相乘，得到大小为 $1×d$ 的矩阵，再和大小为 $d×d_h$ 的矩阵 $W_v$ 相乘，得到大小为 $1×d_h$ 的矩阵，最后和大小为 $d_h×d$ 的 $W_o$ 矩阵相乘，得到最终大小为 $1×d$ 的输出结果:

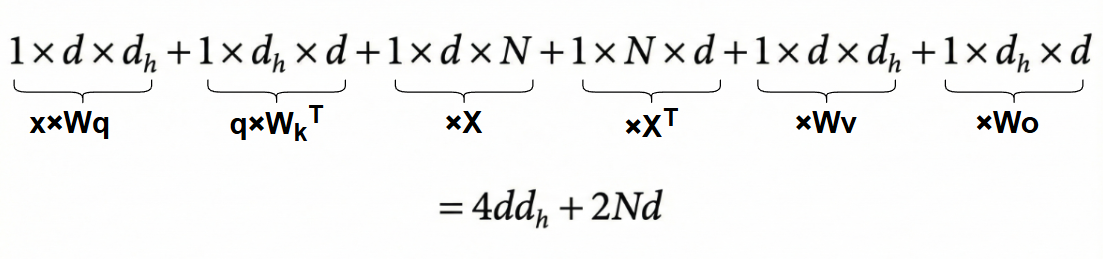
​ 可以发现除了最后和Wo计算，前面就是attention，因此，X Cache也能相对于非KV Cache把时间复杂度从 $O(N^2)$ 降低到 $O(N)$，但是相比于KV Cache来说，attention计算其实是增加了 $O(N(d-d_h))$。

2.1 MLA

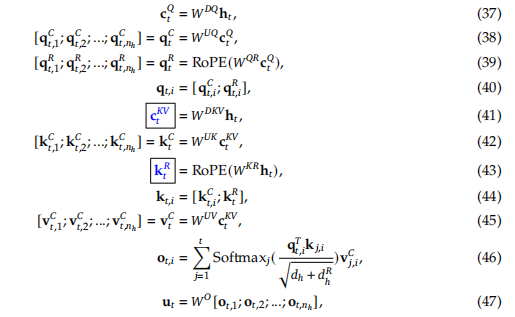
​ 首先公式(37),(38),是将上一层的输入 $h_t$ 进行降维再升维的操作，即对原来的 $W_q$ 矩阵进行降秩。其中 $n_h$ 表示n个attention头。公式(39)即对降维后的 $h_t$，乘以矩阵 $W^{QR}$,计算得到q经过RoPE处理后的带有position信息的矩阵，紧接着公式(40)就是对两个矩阵进行拼接，从而得到完整的q矩阵，公式(41)则是计算一个缓存的c矩阵，这个矩阵就是对 $h_t$ 降维得到的，$W^{DKV}$ 和 $W^{UK}$ 两个矩阵实际就是为了降秩，使得降低保存的c矩阵的显存。下次计算时，只需要取之前缓存的c和当前第t个token计算出来的c拼接后，再用 $W^{UK}$ 升维，得到 $k^{C}$ 矩阵，而k的position信息也单独用一个矩阵保存，并且所有头共享这一个position矩阵，即每个头下，对k矩阵，$k^{R}$ 部分都是完全一样的。需要用到V时，也同样通过对c矩阵升维得到。最后根据公式计算attention和输出。

​ 上面是整个MLA公式项的解读，而实际计算时，会用到矩阵乘法链路最优策略，实际计算过程如下：

​ 第二项就直接根据MQA的方式，广播 $k^{R}$ 矩阵分别和每个头的 $q^{R}$ 矩阵做计算。而第一项按照下方的矩阵吸收的方法算：

​ 实际在代码执行时，是从左往右的顺序计算，免除了计算恢复一个大的K矩阵的问题，V也用同样的方法。

​ 具体MLA代码如下：

class MLA(nn.Module):
    """
    Multi-Head Latent Attention (MLA) Layer.

    Attributes:
        dim (int): Dimensionality of the input features.
        n_heads (int): Number of attention heads.
        n_local_heads (int): Number of local attention heads for distributed systems.
        q_lora_rank (int): Rank for low-rank query projection.
        kv_lora_rank (int): Rank for low-rank key/value projection.
        qk_nope_head_dim (int): Dimensionality of non-positional query/key projections.
        qk_rope_head_dim (int): Dimensionality of rotary-positional query/key projections.
        qk_head_dim (int): Total dimensionality of query/key projections.
        v_head_dim (int): Dimensionality of value projections.
        softmax_scale (float): Scaling factor for softmax in attention computation.
    """
    def __init__(self, args: ModelArgs):
        super().__init__()
        self.dim = args.dim
        self.n_heads = args.n_heads
        self.n_local_heads = args.n_heads // world_size
        self.q_lora_rank = args.q_lora_rank
        self.kv_lora_rank = args.kv_lora_rank
        self.qk_nope_head_dim = args.qk_nope_head_dim
        self.qk_rope_head_dim = args.qk_rope_head_dim
        self.qk_head_dim = args.qk_nope_head_dim + args.qk_rope_head_dim
        self.v_head_dim = args.v_head_dim

        if self.q_lora_rank == 0:
            self.wq = ColumnParallelLinear(self.dim, self.n_heads * self.qk_head_dim)
        else:
            self.wq_a = Linear(self.dim, self.q_lora_rank)
            self.q_norm = RMSNorm(self.q_lora_rank)
            self.wq_b = ColumnParallelLinear(self.q_lora_rank, self.n_heads * self.qk_head_dim)
        self.wkv_a = Linear(self.dim, self.kv_lora_rank + self.qk_rope_head_dim)
        self.kv_norm = RMSNorm(self.kv_lora_rank)
        self.wkv_b = ColumnParallelLinear(self.kv_lora_rank, self.n_heads * (self.qk_nope_head_dim + self.v_head_dim))
        self.wo = RowParallelLinear(self.n_heads * self.v_head_dim, self.dim)
        self.softmax_scale = self.qk_head_dim ** -0.5
        if args.max_seq_len > args.original_seq_len:
            mscale = 0.1 * args.mscale * math.log(args.rope_factor) + 1.0
            self.softmax_scale = self.softmax_scale * mscale * mscale

        if attn_impl == "naive":
            self.register_buffer("k_cache", torch.zeros(args.max_batch_size, args.max_seq_len, self.n_local_heads, self.qk_head_dim), persistent=False)
            self.register_buffer("v_cache", torch.zeros(args.max_batch_size, args.max_seq_len, self.n_local_heads, self.v_head_dim), persistent=False)
        else:
            self.register_buffer("kv_cache", torch.zeros(args.max_batch_size, args.max_seq_len, self.kv_lora_rank), persistent=False)
            self.register_buffer("pe_cache", torch.zeros(args.max_batch_size, args.max_seq_len, self.qk_rope_head_dim), persistent=False)

    def forward(self, x: torch.Tensor, start_pos: int, freqs_cis: torch.Tensor, mask: Optional[torch.Tensor]):
        """
        Forward pass for the Multi-Head Latent Attention (MLA) Layer.

        Args:
            x (torch.Tensor): Input tensor of shape (batch_size, seq_len, dim).
            start_pos (int): Starting position in the sequence for caching.
            freqs_cis (torch.Tensor): Precomputed complex exponential values for rotary embeddings.
            mask (Optional[torch.Tensor]): Mask tensor to exclude certain positions from attention.

        Returns:
            torch.Tensor: Output tensor with the same shape as the input.
        """
        bsz, seqlen, _ = x.size()
        end_pos = start_pos + seqlen
        if self.q_lora_rank == 0:
            q = self.wq(x)
        else:
            q = self.wq_b(self.q_norm(self.wq_a(x)))
        q = q.view(bsz, seqlen, self.n_local_heads, self.qk_head_dim)
        q_nope, q_pe = torch.split(q, [self.qk_nope_head_dim, self.qk_rope_head_dim], dim=-1)
        q_pe = apply_rotary_emb(q_pe, freqs_cis)
        kv = self.wkv_a(x)
        kv, k_pe = torch.split(kv, [self.kv_lora_rank, self.qk_rope_head_dim], dim=-1)
        k_pe = apply_rotary_emb(k_pe.unsqueeze(2), freqs_cis)
        if attn_impl == "naive":
            q = torch.cat([q_nope, q_pe], dim=-1)
            kv = self.wkv_b(self.kv_norm(kv))
            kv = kv.view(bsz, seqlen, self.n_local_heads, self.qk_nope_head_dim + self.v_head_dim)
            k_nope, v = torch.split(kv, [self.qk_nope_head_dim, self.v_head_dim], dim=-1)
            k = torch.cat([k_nope, k_pe.expand(-1, -1, self.n_local_heads, -1)], dim=-1)
            self.k_cache[:bsz, start_pos:end_pos] = k
            self.v_cache[:bsz, start_pos:end_pos] = v
            scores = torch.einsum("bshd,bthd->bsht", q, self.k_cache[:bsz, :end_pos]) * self.softmax_scale
        else:
            wkv_b = self.wkv_b.weight if self.wkv_b.scale is None else weight_dequant(self.wkv_b.weight, self.wkv_b.scale, block_size) 
            wkv_b = wkv_b.view(self.n_local_heads, -1, self.kv_lora_rank)
            q_nope = torch.einsum("bshd,hdc->bshc", q_nope, wkv_b[:, :self.qk_nope_head_dim])
            self.kv_cache[:bsz, start_pos:end_pos] = self.kv_norm(kv)
            self.pe_cache[:bsz, start_pos:end_pos] = k_pe.squeeze(2)
            scores = (torch.einsum("bshc,btc->bsht", q_nope, self.kv_cache[:bsz, :end_pos]) +
                      torch.einsum("bshr,btr->bsht", q_pe, self.pe_cache[:bsz, :end_pos])) * self.softmax_scale
        if mask is not None:
            scores += mask.unsqueeze(1)
        scores = scores.softmax(dim=-1, dtype=torch.float32).type_as(x)
        if attn_impl == "naive":
            x = torch.einsum("bsht,bthd->bshd", scores, self.v_cache[:bsz, :end_pos])
        else:
            x = torch.einsum("bsht,btc->bshc", scores, self.kv_cache[:bsz, :end_pos])
            x = torch.einsum("bshc,hdc->bshd", x, wkv_b[:, -self.v_head_dim:])
        x = self.wo(x.flatten(2))
        return x

​

2.3 MLA的一些疑问记录

​ 1.为什么q的position矩阵，每个attention头都保存，而k的position矩阵只有一个，其它head头共享？

​ 答：原因是对于k来说，这个 $K^{R}$ 是需要缓存的，如果所有head头都用不同的 $K^{R}$ ,那会大幅度增加显存，而 $Q^{R}$ 本身就要计算，并不缓存，那么为了保存更多信息，不影响效率，因此让 $K^{R}$ 做了妥协，而 $Q^{R}$ 仍保留更多信息。

​ 2.为什么MLA存在两种实现，即训练的时候类似MHA，而推理的时候类似MQA？

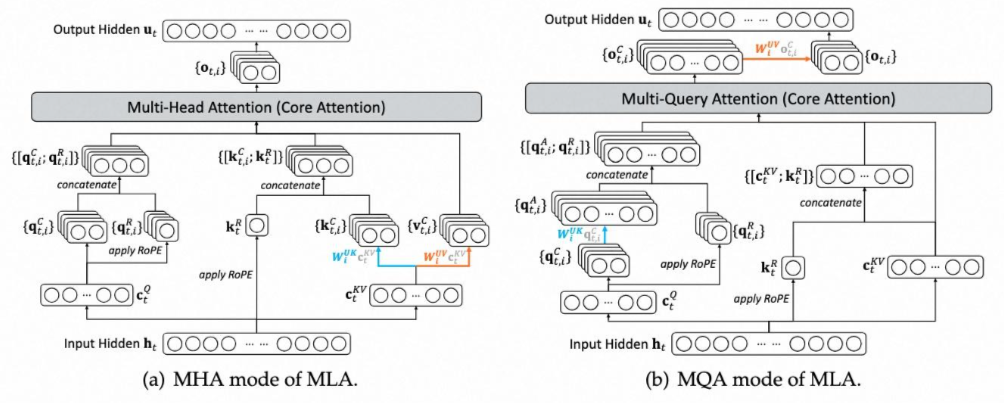
​ 答：因为在训练的时候不需要kv cache，所有token都是并行统一计算的，因此会计算出Q,K,V矩阵，然后计算对应的attention score，而在推理阶段，MLA采用矩阵吸收的思想，把Wk矩阵，即升维那一步的矩阵给吸收到了Q矩阵的计算过程，因此只需要存$c^{KV}_t$这一份数据即可，此时所有Q矩阵共用这一份数据，所以看起来就是MQA。